Compiler 2: Regrex, Finite Automata
- Compilers
- 2025-09-25
- 376 Views
- 0 Comments
- 1356 Words
语言运算


Regular Expression 形式语言

For describing Languages / Patterns
if, else, ...
形式化定义正则表达式(regular expression, regexp),给出了一系列归纳规则(induction rules)
Basic
$\epsilon$ is a regexp, $L(\epsilon) = {\epsilon}$
And if a is a symbol in $\Sigma$, then a is a regexp and $L(a) = {a}$
$\epsilon$ 是一个正则表达式,表示只包含空串的语言。
若 $a \in \Sigma$(符号表),则 $a$ 是正则表达式,表示语言 ${a}$。
Induction
Union
$(r)|(s)$ is a regexp denoting the language $L(r) \cup L(s)$
$(r)(s)$ denotes $L(r)L(s)$
$(r)^$ denotes $(L(r))^$
$r = (r)$
给出如何从已有的正则表达式构造新的正则表达式:
- 并 (Union):$(r)|(s)$ → $L(r) \cup L(s)$
- 连接 (Concatenation):$(r)(s)$ → $L(r)L(s)$
- Kleene star:$(r)^$ → $(L(r))^$
- 括号 (Parentheses):如果 $r$ 是正则表达式,那么 $(r)$ 也是正则表达式,且 $L((r)) = L(r)$。
优先级 Precedence
closure* > concatenation > union
结合性 Associativity
左结合的 $a|b|c = (a|b) | c$
例子
$\Sigma = {a,b}$
$a|b$ denotes {a,b}
$(a|b)(a|b)$ denotes {aa, ab, ba, bb}
$a^$ denotes ${\epsilon, a, aa, aaa, ...}$ (这里*就是任意大于等于0的数目,$a^0, a^1, ...$)
$(a|b)^$
A regular language is a language that can be defined by a regexp
• If two regexps r and s denote the same language, they are equivalent,
written as r = s

Regular Definitions(正规定义/正则定义)
这是编译原理里 词法规则书写的一种方式,通常结合正则表达式(Regular Expressions, RE)来描述。
1. 定义
-
Regular Definition 是一种“命名规则”的机制:
我们可以用符号/名字给一个正则表达式(Pattern)起别名,后续在更复杂的规则中直接使用这个名字。 -
它其实就是 正则表达式的宏定义。
2. 形式
通常写作:
D → rD:定义的名字(类似宏/变量名)r:一个正则表达式
3. 示例
在词法分析器里,很多语言会这么定义:
letter → A | B | ... | Z | a | b | ... | z
digit → 0 | 1 | ... | 9
id → letter (letter | digit)*
number → digit+解释:
letter定义了“字母”的正则模式。digit定义了“数字”的正则模式。id定义了 标识符:必须以字母开头,后面跟任意多个字母或数字。number定义了 数字:由一个或多个数字组成。
这样,当你写复杂规则时,不用每次都写长长的表达式,而是用名字简化。
4. 在编译器工具中的应用
-
在 Lex/Flex 工具中,就经常会用到 Regular Definitions:
DIGIT [0-9] ID [a-zA-Z][a-zA-Z0-9]* %% {DIGIT}+ { printf("NUM\n"); } {ID} { printf("IDENTIFIER\n"); } %% - 这里
DIGIT、ID就是 Regular Definitions。 - 在规则部分
{DIGIT}+、ID就可以直接使用。
5. 和 Regular Expression 的区别
- Regular Expression(正则表达式):是模式本身,用来描述字符集/语言。
- Regular Definition(正规定义):给正则表达式起名字,方便复用。
👉 可以理解为:
- RE = 具体的公式
- RD = 定义公式的变量
✅ 一句话总结:
Regular Definitions 就是 把正则表达式起名字,像数学里给复杂公式设变量一样,用来简化词法规则的书写。
从 letter/digit → id/number → token
C identifiers
标识符是用户定义的名称,用于方便引用内存。它还用于定义程序中的各种元素,例如函数、用户定义类型、标签等。因此,标识符是帮助程序员更便捷地使用编程元素的名称。

Finite Automata
有穷自动机

NFA
NFA(Nondeterministic Finite Automaton,非确定有限自动机)是编译原理里用于形式化描述正则语言的重要数学模型。它和 DFA(确定有限自动机)类似,但在状态转移时允许非确定性选择(同一个输入符号可能对应多个后继状态,也允许 ε-转移)。
一个 NFA 定义为一个五元组:
$M = (Q, \Sigma, \delta, q_0, F)$
- 自然数可数,但是无穷。要一个这个state
- input alphabet
- transition function
- start state
- accepting state

图中的 nondeterminism: 在状态转移时允许非确定性选择(同一个输入符号可能对应多个后继状态,也允许 ε-转移)
(0,a): 我们看到我们在状态0,下一个字母是a,我们可以走0或者1
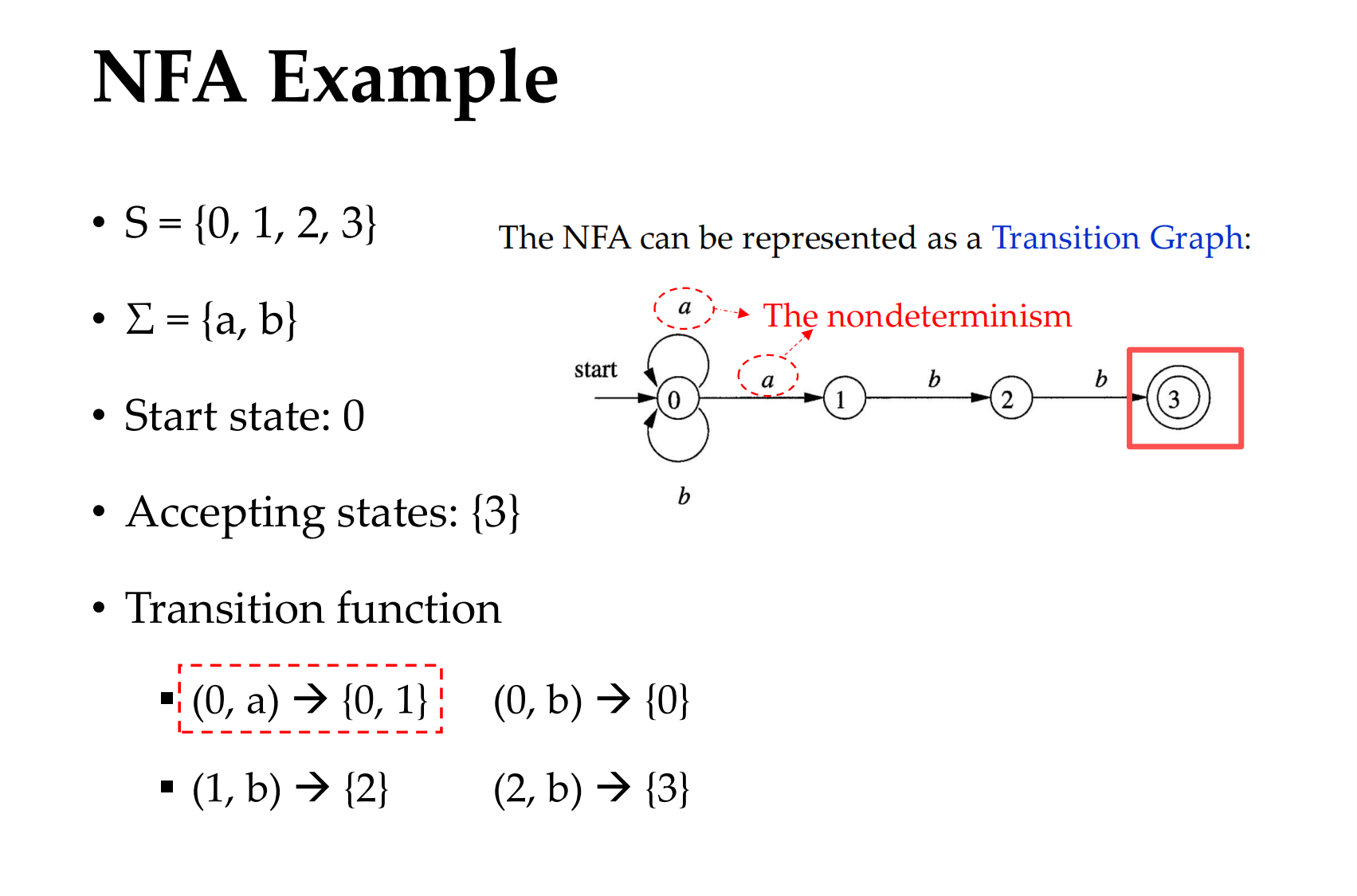
状态转换图
note: it's possible to have $\epsilon$ moves (not using a,b,c, etc)
状态转换表:

$\phi$ means error/can't go there
For string x, NFA starts from a state, then ends at one ending state, then we say NFA accept this x

a a b b = $L((a|b)^* abb)$
what would happen if you go another path
how to translate the graph:
$a^ | b^$
$\epsilon a a | \epsilon b b$ = a+|b+
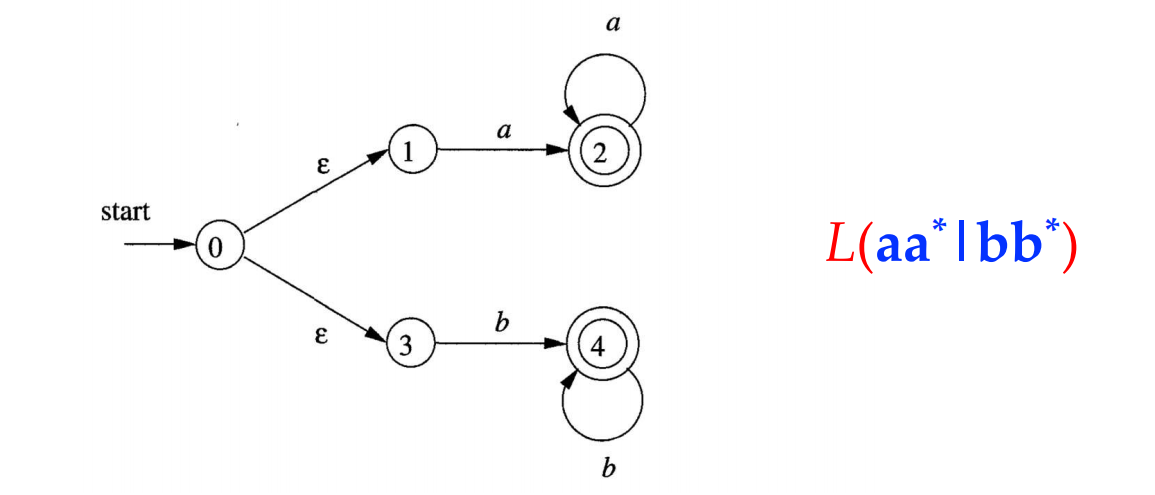
DFA
DFA is a special NFA.
For every new symbol, we can only have one target state. 一个symbol只能走到一个特定状态
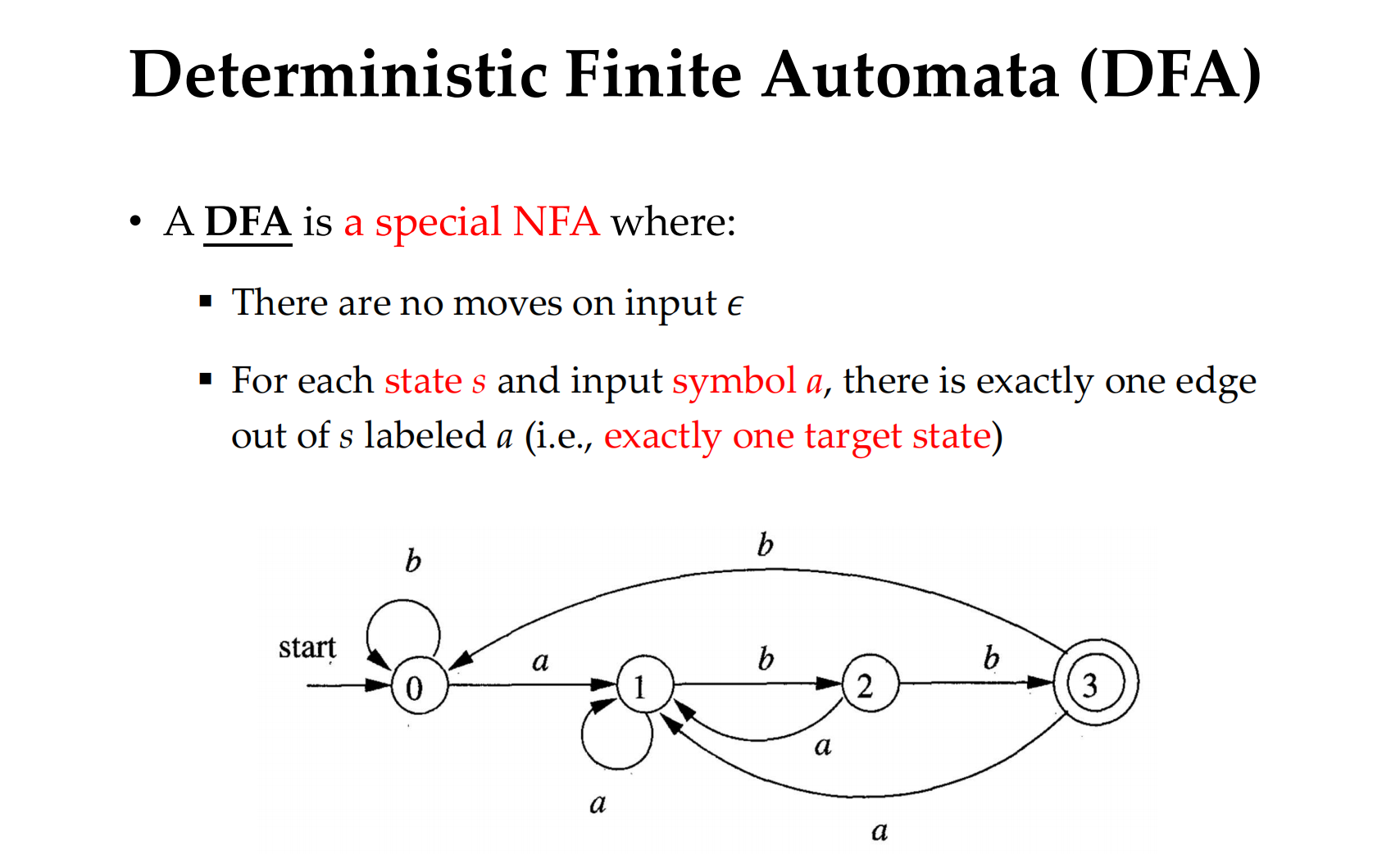
A good algorithm for simulating a DFA
time complexity: $O(n)$ , n denotes for length of string

DFA的问题problem: too complex for regular expression
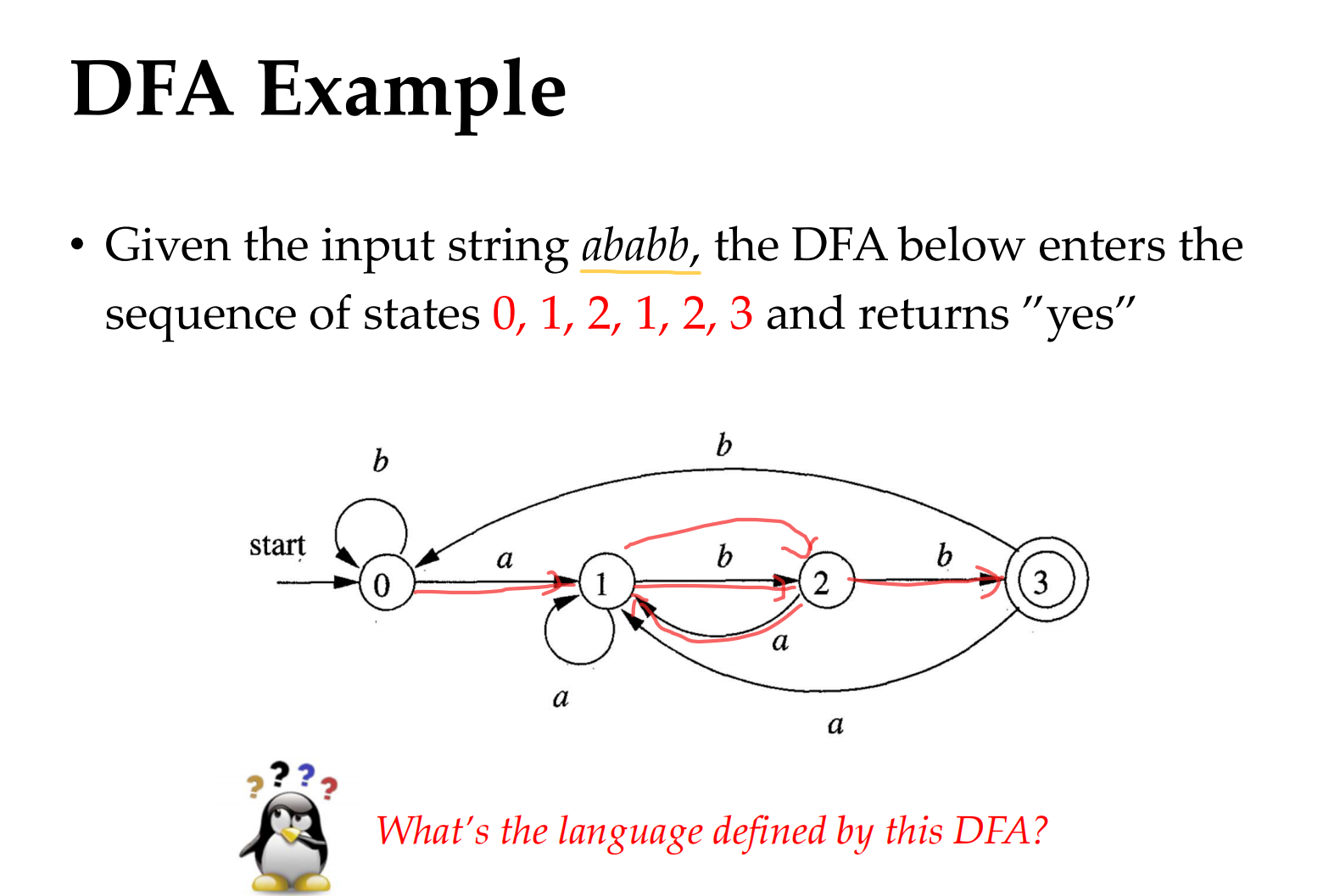
build lexical analyser NFA->DFA
path explosion

why reg->NFA->DFA? why not Reg->DFA?
Too complex
So we have 2 algorithms: Thompson's construction+subset construction
Subset construction: expand solutions.

you can go to 3,6,1,2,7,4,8, by reading a.

move: from a state to another state

注意这里的 $if(u is not in \epsilon-closure(T))$ 如果存在一个自身连着并且是epsilon的边,就可以省略
So $\epsilon-closure(0) = {0,1,7,2,4}$
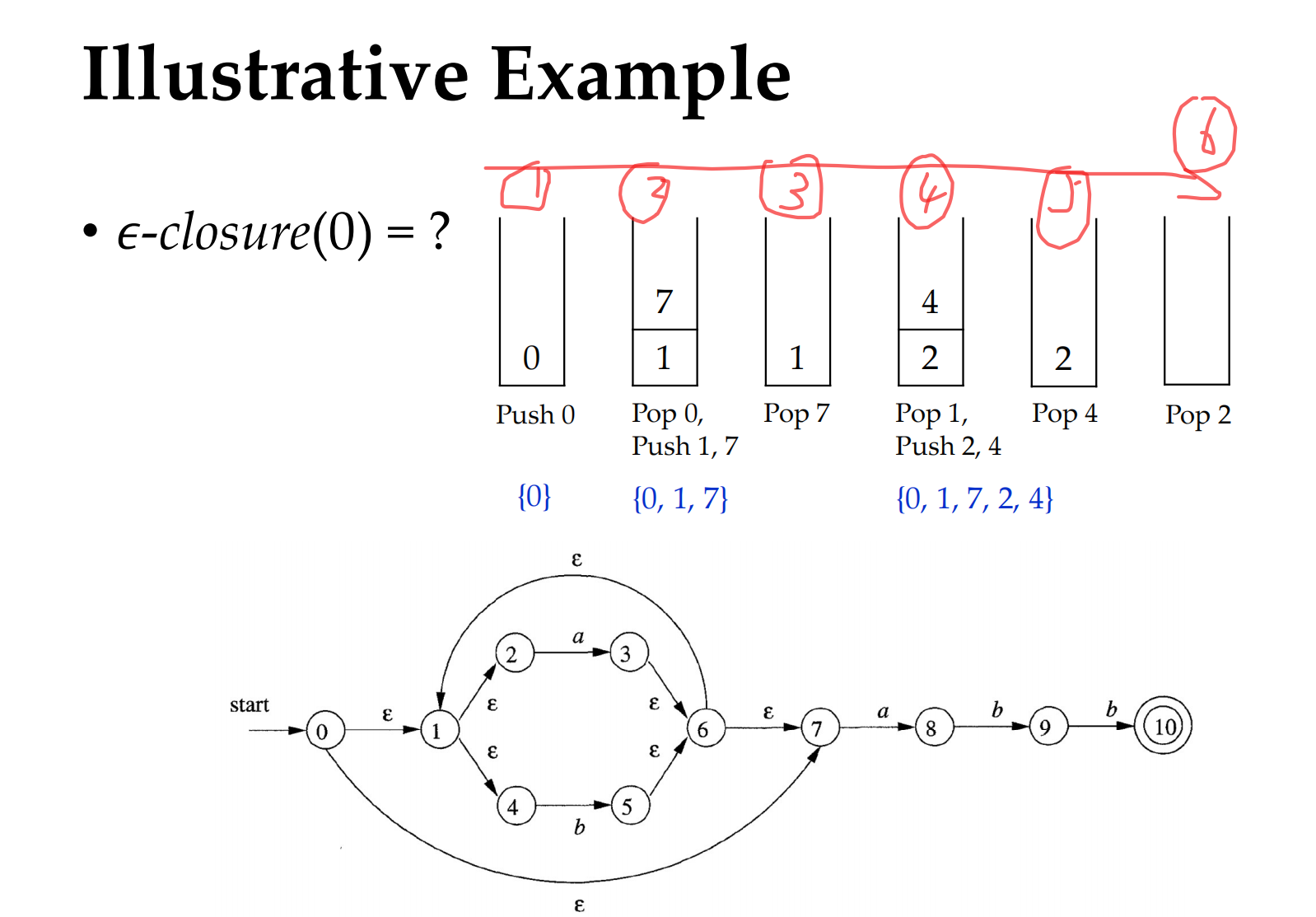
我们在找等价状态
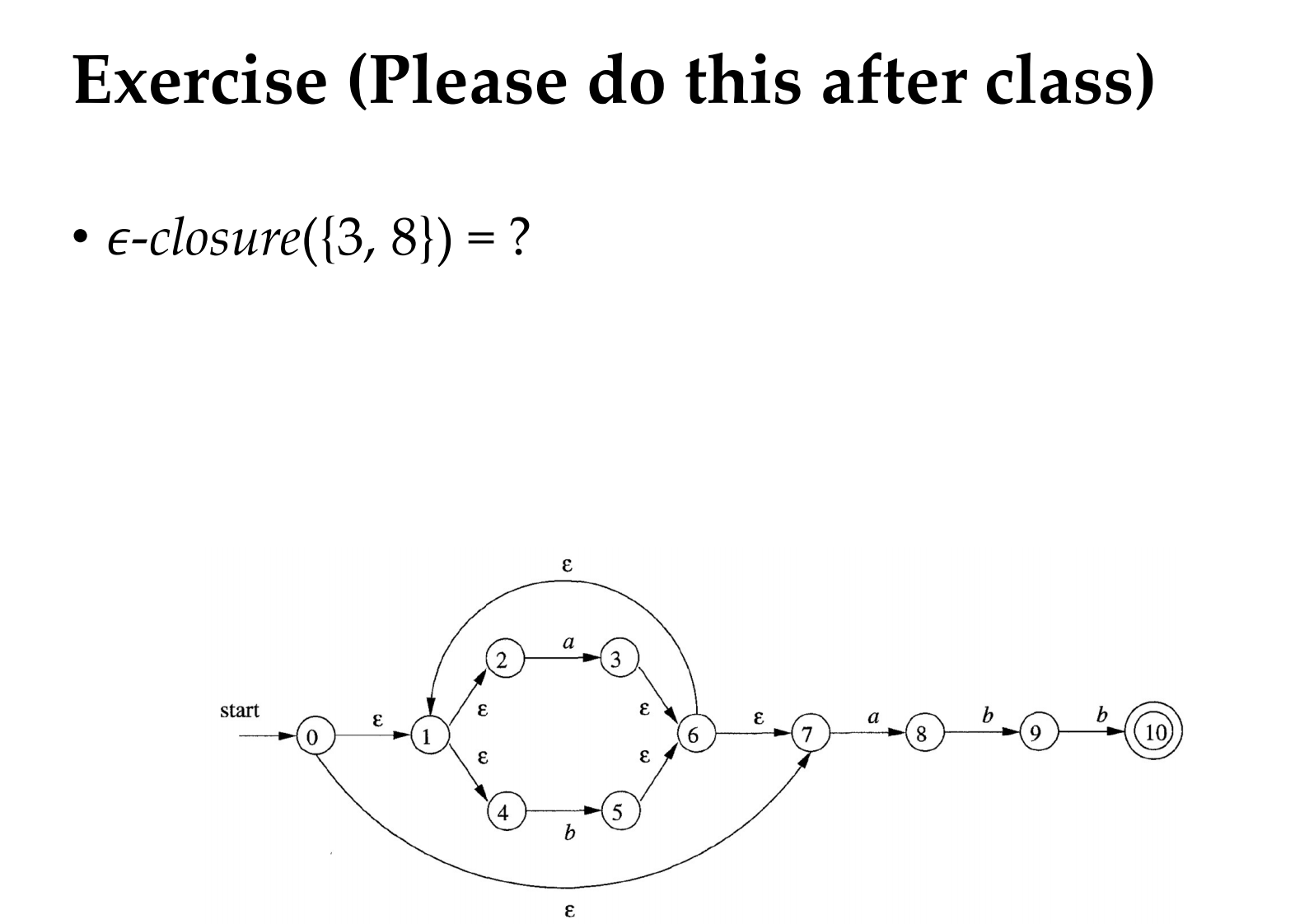

NFA → DFA 的子集构造法之所以是一个不动点计算,是因为我们在有限状态集合上迭代一个单调扩展算子 FFF,直到达到“稳定状态” F(C)=CF(C) = CF(C)=C。这个稳定状态就是所有可达的 DFA 状态集合,也就是子集构造的最终结果。
