现在位置: 首页 / Paper Reading / I/O / 正文

STOC81 I/O Complexity: The Red-Blue Pebble Game

STOC81 I/O Complexity: The Red-Blue Pebble Game

这是一篇理论计算机科学文章，但是描述了一个非常有趣的问题：就像时间复杂度一样，我们能不能做一个I/O复杂度，衡量一个程序最少要进行多少次I/O?

文章链接：
https://www.eecs.harvard.edu/~htk/publication/1981-stoc-hong-kung.pdf

Compute不贵，I/O才贵

随着现代的CPU、GPU、xPU越来越强，越来越多workload性能瓶颈出现在memory上。比起浮点性能，人们开始关注数据在不同存储层级之间的移动。

在谈论矩阵乘法的性能时，我们往往习惯于从计算量出发：一个 N×N 的矩阵乘法需要 2N^3 次浮点运算。而在内存数据的背景下，一个问题随之出现： 一个算法在理想情况下，究竟“最少”需要搬运多少数据？

为了搞清楚这个问题，今天我们来看一篇在 IO 方向的开山之作：I/O COMPLEXITY: THE RED-BLUE PEBBLE GAME。

这篇文章引入了一个 “I/O复杂度“ 的概念，证明在一个有两层结构memory的计算系统中（比如GPU的DRAM与L2 Cache），如果我们的高速缓存大小是S，不考虑低速内存大小的影响，那么我们在计算大小为 NxN的矩阵乘法时，我们需要搬运 $O(N^3 / S^{0.5})$ 的数据搬运量。

This paper proposes a pebble game, called the red-blue pebble game, to model the problem, and presents a number of lower bound results for the I/O requirement.
image.png

The Pebble Game Idea

As the usual pebble game (see, e.g. [4]), the red-blue pebble game is played on a directed acyclic graph. 1 At any point in the pebble game, some vertices of the graph will have red pebbles, some will have blue pebbles, some will have both red and blue pebbles and the remainder will have no pebbles at all.

文章把一个程序访问内存抽象成一个这样的模型：

  • 🔴 红色鹅卵石 pebble = fast memory（cache / SRAM / HBM）
  • 🔵 蓝色鹅卵石 pebble = slow memory（DRAM / SSD）
  • 🧩 计算过程 = 一个 DAG（计算图）
    • 节点 = 一个中间数据 / 一次计算
    • 边 = 数据依赖

The set of inputs (or outputs) of the graph is some designated set of vertices containing at least those vertices that have no predecessors (or successors, respectively). We assume that the set of inputs is disjoint from that of outputs. For all the examples discussed in the paper, only vertices that have no predecessors (or successors) are assumed to be inputs (or outputs, respectively), except in Section 7 where products of graphs are considered. The initial (or terminal) configuration is one in which only inputs (or outputs, respectively) have pebbles, and they are all blue pebbles.

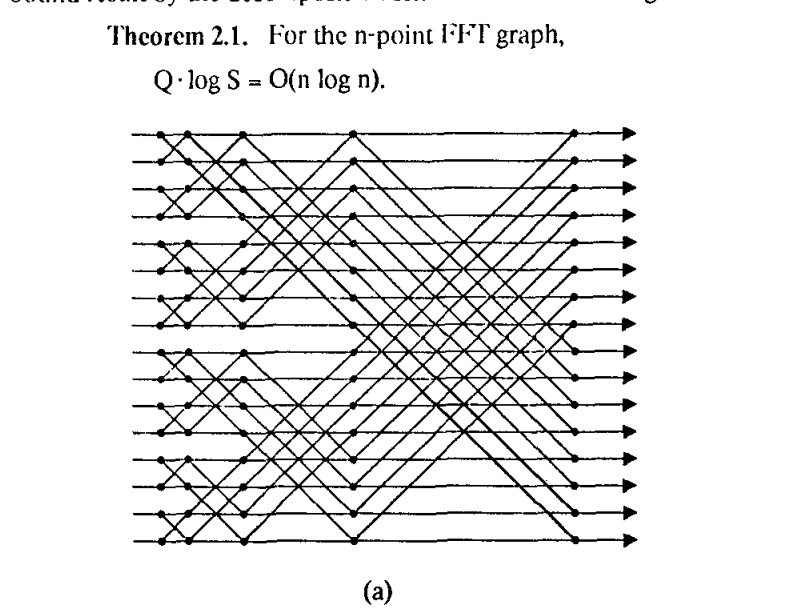
比如这个是FFT的计算图
image.png
在我们的游戏里，有4个规则：

  • R1：Load（蓝 → 红）
    从慢内存把一个数据搬到快内存
  • R2：Store（红 → 蓝）
    把快内存的数据写回慢内存
  • R3：Compute（计算）
    如果一个节点的所有输入都在红色（cache）里，就可以计算它，并把结果放在红色里
  • R4：Delete（删除）
    从红或蓝里删除一个数据（释放空间）

在实际计算模型时，我们会把程序DAG就变成一个桌游，你的目标是走完这个桌游。所有的数据初始都是蓝宝石，然后你必须先把它挪到红宝石Load，再计算Compute，然后再Store，变回到蓝宝石。

同时我们限制Cache的大小。也就是说，在同一时刻，DAG内红宝石的数量是有限的：

  • 🔴 红 pebble 数量 ≤ S
    → 表示 cache 只能装 S 个数据
  • 🔵 蓝 pebble 不限
    → 表示内存很大

GPT给的例子：计算 c = a + b

文章里给的是FFT快速傅立叶变换的例子，并且不加解释的直接给IO下限。我觉得不好解释，就换成最简单的例子了。

DAG：

a   b
 \ /
  +
  |
  c

初始状态：

  • a, b 在蓝色（内存）
  • cache 里什么都没有

Step 1：把 a load 进 cache

R1：a 上放红 pebble（蓝 → 红）

现在：

  • 红：a
  • 蓝：a, b

Step 2：把 b load 进 cache

R1：b 上放红 pebble

现在：

  • 红：a, b

  • 蓝：a, b

    Step 3：做加法

    R3：因为 + 的两个输入（a, b）都有红 pebble，可以计算 +

    • 节点放一个红 pebble（结果在 cache）

Step 4：把结果 c 写回内存

R2：在 c 上放一个蓝 pebble

Step 5：释放 cache

R4：删掉 a, b, + 上的红 pebble

在这个过程中：

  • R1 用了 2 次（load a, load b）
  • R2 用了 1 次（store c）
  • R3 用了 1 次（compute）
  • R4 若干（不计入 I/O）

我们这里就简单演示了我们的DAG流下程序在模型的运行情况。

这里，文章定义：我们的IO次数Q就是 R1 和 R2 之和

For any given graph, we are interested in the minimum 1/0 time Q, which is defined by Q = the minimum number of transitions according to role R1 or R2 required by any complete calculation.

如何证明矩阵乘法的IO下界

S-Partitioning

文章这里用了一个idea/分法 叫 S-Partitioning。

S-Partitioning的idea很像tilling。它想法是把计算图（DAG）切成若干块，每一块都装得进 cache（大小 S），然后用块的数量来下界 I/O 次数。

由于cache 只能放 S 个数据，那么每一“阶段”你最多只能处理一小块子图，整个 DAG 必须被切成很多块。此时 块的数量 × S ≈ 最少 I/O 次数

这里文章也给了几条规则P：

  1. 所有的S-partition {V1, ... ,Vh} 要 不重不漏
  2. 每一块的输入边界 ≤ S（Dominator ≤ S）。cache 最多装 S 个数
  3. 每一块的输出边界 ≤ S（Minimum set ≤ S）cache 最多只能往外“吐”S 个数
  4. 块与块之间的依赖关系必须是 DAG（不能循环）

具体可看原文：
image.png

随后Hong证明，任何用 S 大小 cache 的真实执行过程，一定对应着某个 2S-Partition块。在这个块里，最多只能涉及2S个数据：

因为在真实执行中，一个阶段里：

  • cache 里最多有S 个 旧数据（之前就有的红 pebble）
  • S 个 新 load 进来的数据（通过 R1）

所以最多会涉及 2S 个数据。

image.png

任何使用 ≤ S 个红 pebble 的完整计算过程 都能构造出一个 2S-Partition。并且他们的IO计算次数满足下面的关系：
image.png

进而作者给出了 IO bound Q的下界计算方法：

Q≥S⋅(P(2S)−1)
image.png

至此，文章把一个IO bound计算问题，转换成计算DAG中有多少2S子图的问题。

后面文章内容其实都是根据具体例子计算出一个算法里的2S块有多少，然后给出Q下限了。

I/O Complexity 例子

FFT

原文的显示太糟糕了。我让GPT做了分析。感兴趣的朋友可以读下原文，并且看看GPT说的是否是正确的。

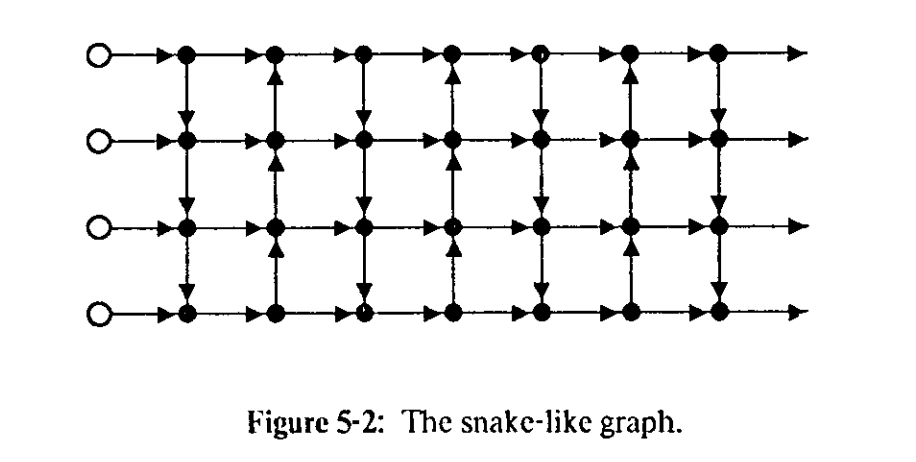
image.png

GPT的分析：
image.png

I/O 难被 cache 改善的情况

有些计算图天生就几乎没有数据复用，因此 I/O 难以被 cache 改善。这个mxn snake-like directed mesh（蛇形网格）。IO下限为 Q=mn （m是这个矩形长度，n是宽度）（在S<m情况下）
image.png
image.png

Matmul

文章证明矩阵乘法IObound如下：

image.png
我们目前的矩阵乘法对内存利用是最优的吗？似乎不是？

文章结论

给出了不同算法的IO bound:
image.png

I/O后续的讨论

给IO访问建立了一个理论模型的第一篇文章。

IO访问一直都是一个瓶颈，比如从能量角度来说，根据HiPEAC 2025一篇文章，一次CPU上内存访问消耗的能量是一次加法的～100至1000倍，ISCA2016的一篇文章显示数据移动的能量更是远远大于计算所需的能量。ASPLOS2018的一篇文章指出在Google消费级设备中，62.7%的整体系统性能花在了数据移动上。而在大型AI模型中，PACT2021的一篇文章发现高于90%的能量都用于内存当中。

992f6d0a72ed9bd97b5dce9074313a6b.png
来自Prof. Onur Mutlu 的课程PPT，https://people.inf.ethz.ch/omutlu/

Hong-Kung下限是最终目前确定的下限吗？

Sadayappan 教授曾总结过这个问题。目前最新的下限如他文章所说。目前的最低下限由这篇文章得出：Smith T M, Lowery B, Langou J, et al. A Tight I/O Lower Bound for Matrix Multiplication[J]. 2017
image.png

这篇文章为 后摩尔时代高性能软件开发的挑战 ，在中国计算机学会通讯 第 15 卷  第 10 期  2019 年 10 月 有翻译。

一篇MIT与NV的ISCA24 的文章也探讨过这个问题：Mind the Gap: Attainable Data Movement and Operational Intensity Bounds for Tensor Algorithms （好像还是best paper）

PPT:
https://hqjenny.com/papers/2024ISCA/2024ISCA_Orojensis_Presentation.pdf

Paper:
https://people.csail.mit.edu/emer/media/papers/2024.06.isca.orojenesis.pdf

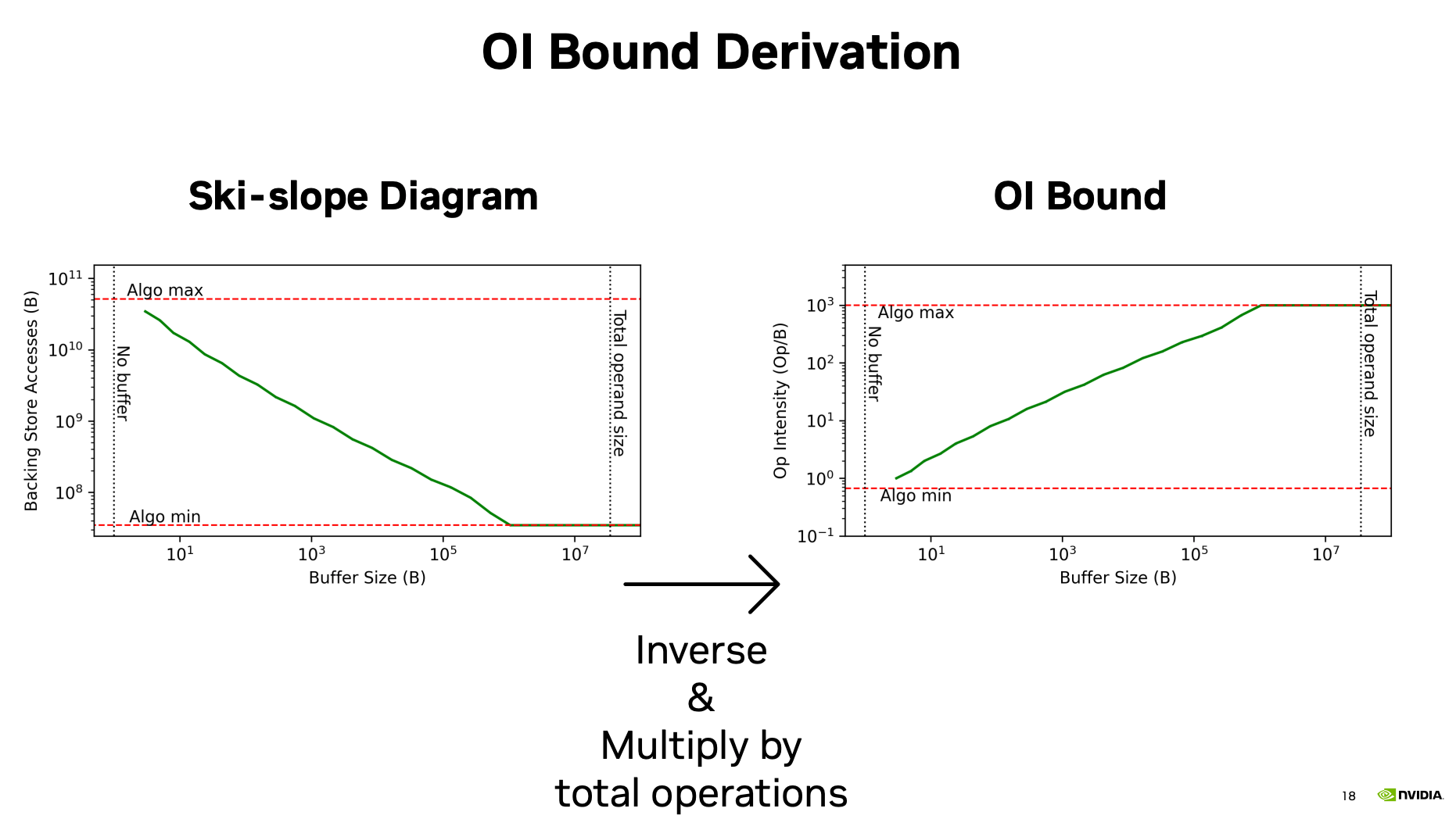
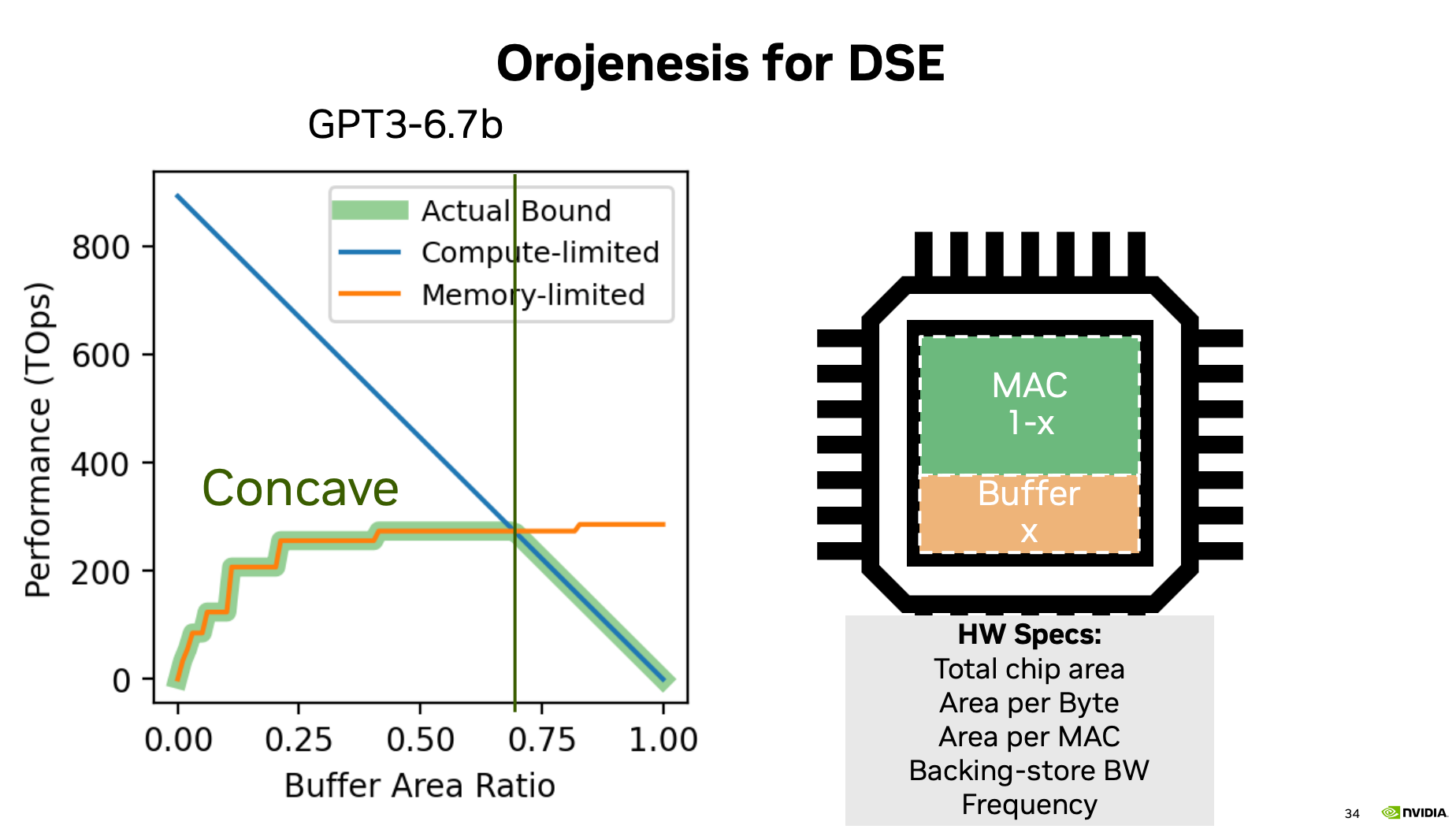
文章在讨论，在芯片设计时，buffer/Cache的可以减少慢内存访问。但是Cache设计多大，不知道。同时，kernel融合后，能不能更好的依赖cache，值得研究。

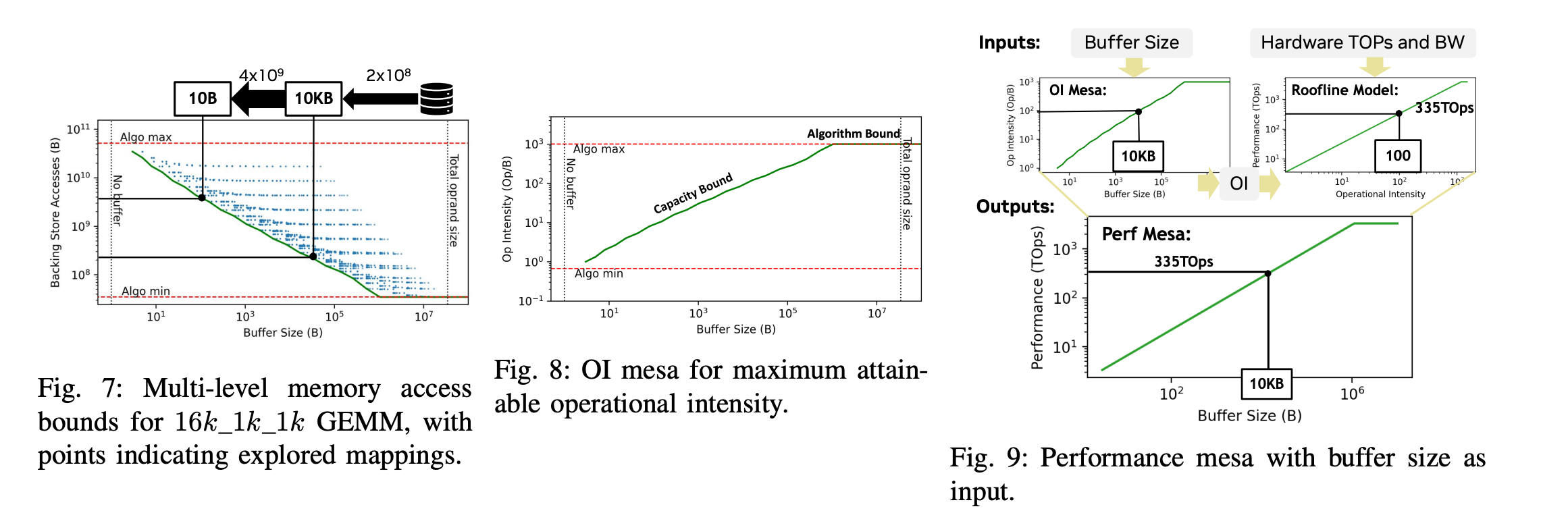
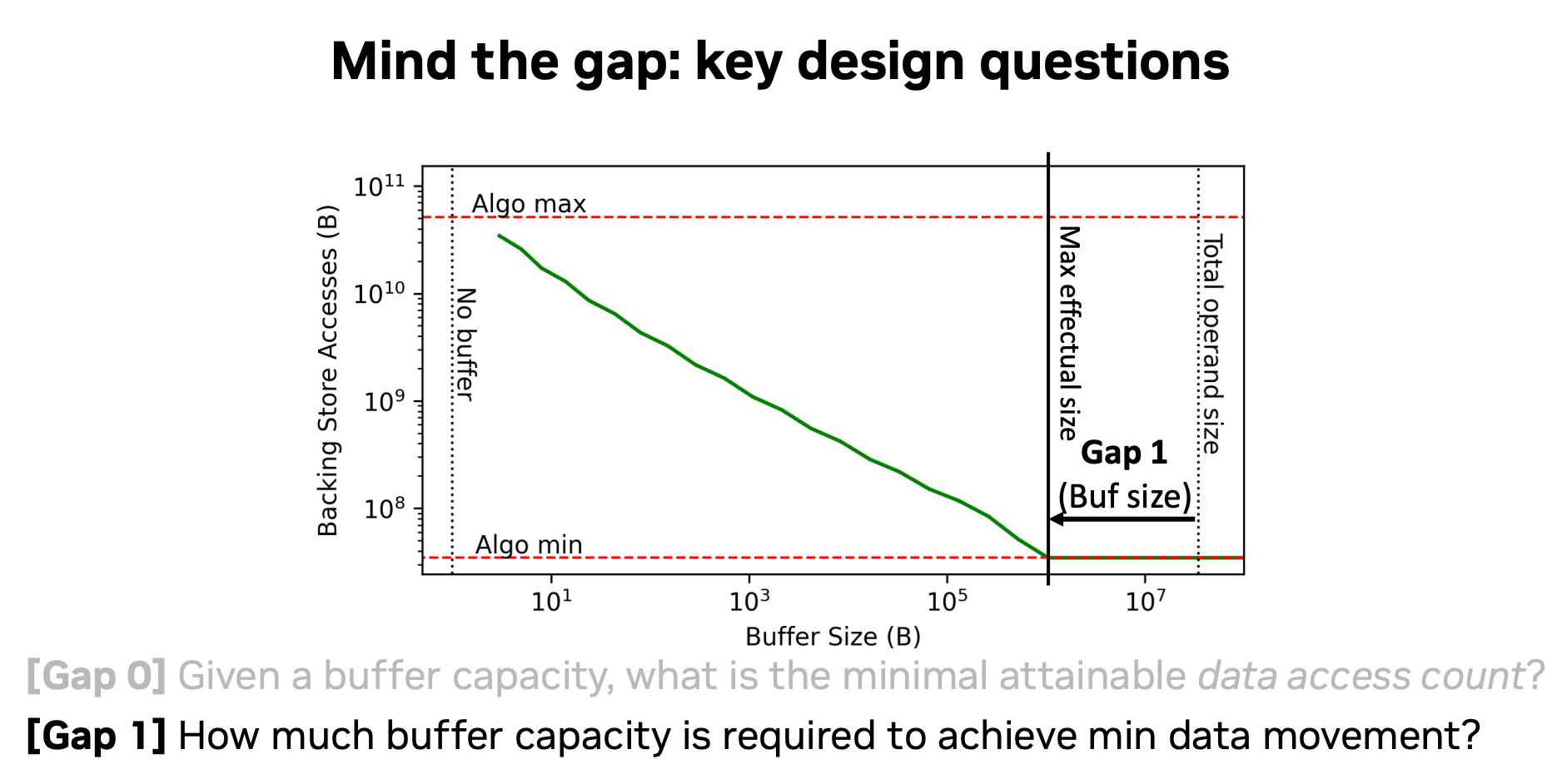
image.png

image.png

不过，我觉得最值得注意的是这张图：
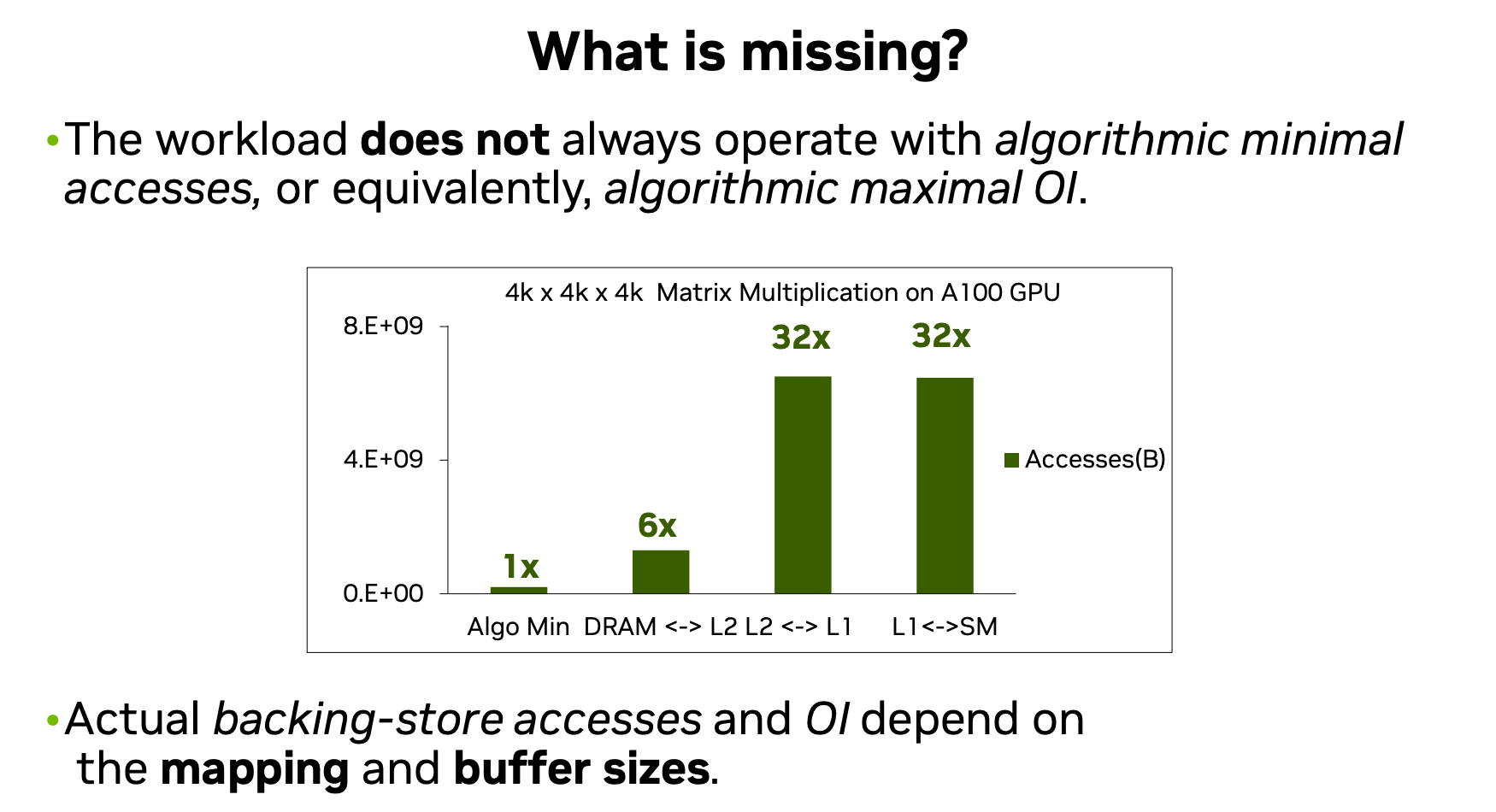
image.png

它告诉我们，其实我们的IO读取量，离最低IO访问还差很远。还有很多可以优化的。软件上的优化路还很长。

image.png
image.png