Hungarian Algorithm

Algorithm Design and Analysis (H) Assignment 5

Name: 赖海斌

SID: 12211612

Abstract

In this assignment we try to analyze Hungarian algorithm. It’s an efficient algorithm for solving the min-cost max-matching problem in a bipartite graph. It finds a min-cost perfect matching in O(n^3) time.

ADA Assignment5 Haibin Lai
docx

Pseudocode for Hungarian algorithm

 def hungarian(node)
 {
  Count =0;
   for i from 1 to n
    if (dfs\_findPath)
      Count ++;
   return Count ;
 }

def  dfs_findPath(node start)
{   node = start;
    for (search every edge that node    connect）{
    node *To* = the other node that connect to the edge
        if（we haven’t visited *To*）
            Set *To* into visited;
        if (*To* hasn’t been bipartite or *To* can be matched to *now*)
            Match *To*，*now*
    return true;    // we can find a path
}
    //Can not find
    return false；
}

Core idea and critical procedures

The core idea of this algorithm is to gradually construct the maximum matching by continuously searching for augmenting paths. It’s like GS algo to get every node a match then match better like greedy.

In the Hungarian algorithm, an augmenting path is a special path that starts from an unmatched vertex in the current matching and extends by alternately traversing unmatched and matched edges until reaching another unmatched vertex. The length of an augmenting path should be odd because it must begin and end with unmatched vertices.

Hungarian algorithm first search and Discover augmenting paths in the problem. Starting from an unmatched vertex, the algorithm searches by alternately traversing unmatched and matched edges until it reaches another unmatched vertex. It can increase the size of the current matching.

Then Hungarian algorithm Utilizes augmenting paths to update the matching. Once an augmenting path is found, the Hungarian algorithm utilizes it to improve the current matching by updating the edges along the augmenting path.

As we can see from the Pseudocode, the algorithm follows these critical steps:

1. Initialization: Mark all edges as unmatched.

2. Traverse unmatched left vertices: For each unmatched left vertex, attempt to find an augmenting path to find augmenting routes.

3. Find augmenting paths: Start from the current unmatched left vertex and try to match the right vertices one by one. If a right vertex is already matched, recursively look for adjacent unmatched vertices until an unmatched right vertex is found or no new unmatched vertex can be found.

4. Match edges on the augmenting path: Match or unmatch edges on the augmenting path to increase the number of unmatched left vertices.

5. Repeat steps 2 and 4 until no augmenting path can be found.

Ultimately, the Hungarian algorithm can find the maximum matching in a bipartite graph.

Correctness, running time, and space complexity of the algorithm

Hungarian algorithm uses the feature of augmenting paths to reach correctness.

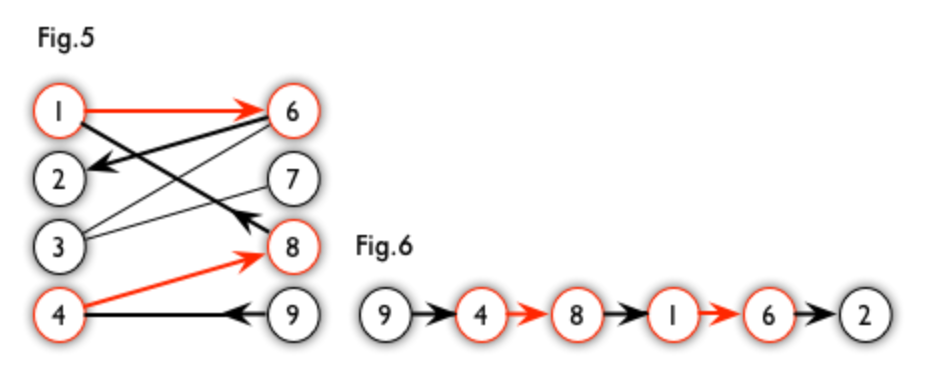
As shown in the diagram, Path 6 is one of the augmenting paths of Graph 5. It can be observed that starting from the unmatched vertex 9, it sequentially follows the edges ( (9, 4) ) -> ( (4, 8) ) -> ( (8, 1) ) -> ( (1, 6) ) -> ( (6, 1) ) to reach the unmatched vertex 1. Clearly, this is an augmenting path.

We can identify some characteristics of augmenting paths:

1. An augmenting path always consists of an odd number of edges.

This is trivial since we need to start from a unmatch node and end in unmatch node with crossing unmatch edge and match edge one by one.

2. In an augmenting path, the number of unmatched edges is always one more than the number of matched edges.

We can proof this since it starts from an unmatched vertex and ends at another unmatched vertex, traversing alternately matched and unmatched edges.

This actually demonstrates the significance of augmenting paths. If an augmenting path is found, by swapping the roles of unmatched vertices and matched edges, the number of matched edges increases by one. This process continues until no augmenting path can be found.

So every time we run one finding on the algorithm, we will find that a new pair every time.

Consequently, the total number of matched edges in the entire graph is maximized, which means the maximum matching of the bipartite graph is achieved. So the algo become correct.

Time Complexity: O(VE)

The implementation of the Hungarian algorithm is based on the vertex set. In each iteration, a vertex ( node ) is chosen as the starting point to search for augmenting paths. Searching for augmenting paths requires traversing all edges in the edge set ( E ), which can be done using DFS or BFS. Regardless of the method chosen, the time complexity remains ( O(E) ).

Each vertex can only be selected once in the Hungarian algorithm since we will mark them. Therefore, the overall time complexity of the algorithm is O(VE) .

Space Complexity: O(V+E)

We need to store the vertex and edge into array. Also, our match is O(E), our visited array is O(V). So in total we have O(V+E) space complexity.

Formulate a max-cost max-matching problem as a min-cost perfect-matching problem

First, let's define the min-cost perfect-matching problem. In a min-cost perfect-matching problem, we aim to find a matching in a bipartite graph that minimizes the total cost while ensuring that each vertex is incident to exactly one edge.

Now, to formulate the max-cost max-matching problem as a min-cost perfect-matching problem, we follow these steps:

Negate the Costs: Negate the costs of all edges in the graph. This converts the max-cost problem into a min-cost problem.

Add Dummy Vertices: If necessary, add dummy vertices and edges with zero cost to ensure that the number of vertices on both sides of the bipartite graph is equal. This step ensures that a perfect matching can be found.

Find the Min-Cost Perfect Matching: Use Hungarian algorithm to find the minimum-cost perfect matching in the modified graph.

Reverse the Costs back: If necessary, reverse the sign of the costs in the obtained matching to obtain the max-cost matching in the original graph.

Explanation of Correctness:

Negating the Costs: By negating the costs, we convert the max-cost problem into a min-cost problem. This is based on the principle that finding the min-cost matching in the modified graph is equivalent to finding the max-cost matching in the original graph.

Adding Dummy Vertices: Adding dummy vertices ensures that a perfect matching can be found, which is necessary for the min-cost perfect-matching problem. These dummy vertices and edges do not affect the final matching's cost in the original graph. And we are benefit from its num since some finding in Hungary cannot pass Negate if we don’t add.

Finding the Min-Cost Perfect Matching: Then we get the problem of Hungary can solve. So we can just use it.

After that, by transforming the max-cost max-matching problem into a min-cost perfect-matching problem and applying standard algorithms for min-cost perfect matching, we can effectively solve the original problem.

Reference

[1] OI WIKI https://oi-wiki.org/graph/graph-matching/bigraph-weight-match/

[2] Algo intro https://www.cnblogs.com/purinliang/p/14501584.html

[3] Intro & code https://xiexuewu.github.io/view/150.html

[4] The Dynamic Hungarian Algorithm for the Assignment Problem with Changing Costs

G. Ayorkor Korsah, Anthony (Tony) Stentz, and M. Bernardine Dias

Tech. Report, CMU-RI-TR-07-27, Robotics Institute, Carnegie Mellon University, July, 2007