现在位置: 首页 / 分布式系统 / Snapshots / 正文

Distributed System 4: Distributed Snapshots

Snapshots: save the data

我们想要捕捉系统在某一时刻 TTT 的一致全局状态，包括：

  • 每个进程的本地状态；
  • 每条通道上的消息状态（即“正在飞”的消息）。

常见应用场景：

  • 检查点恢复（Checkpoint / Rollback Recovery）
  • 检测全局死锁
  • 检测全局不变式（如是否所有账户加和为常数）
  • 调试 / 稳定状态检测（如终止检测）

问题是：

在分布式系统中没有全局时钟，进程之间的消息异步传递，我们无法在同一“时间点”同时拍照。

这就是一致快照问题（Consistent Snapshot Problem）。

比如：

  • P1 在 10:01 拍照；
  • P2 在 10:02 拍照；
  • 如果中间有消息在传递，这两个快照组合起来可能不是系统的真实状态。

Target: markdown every 圈 in the process:
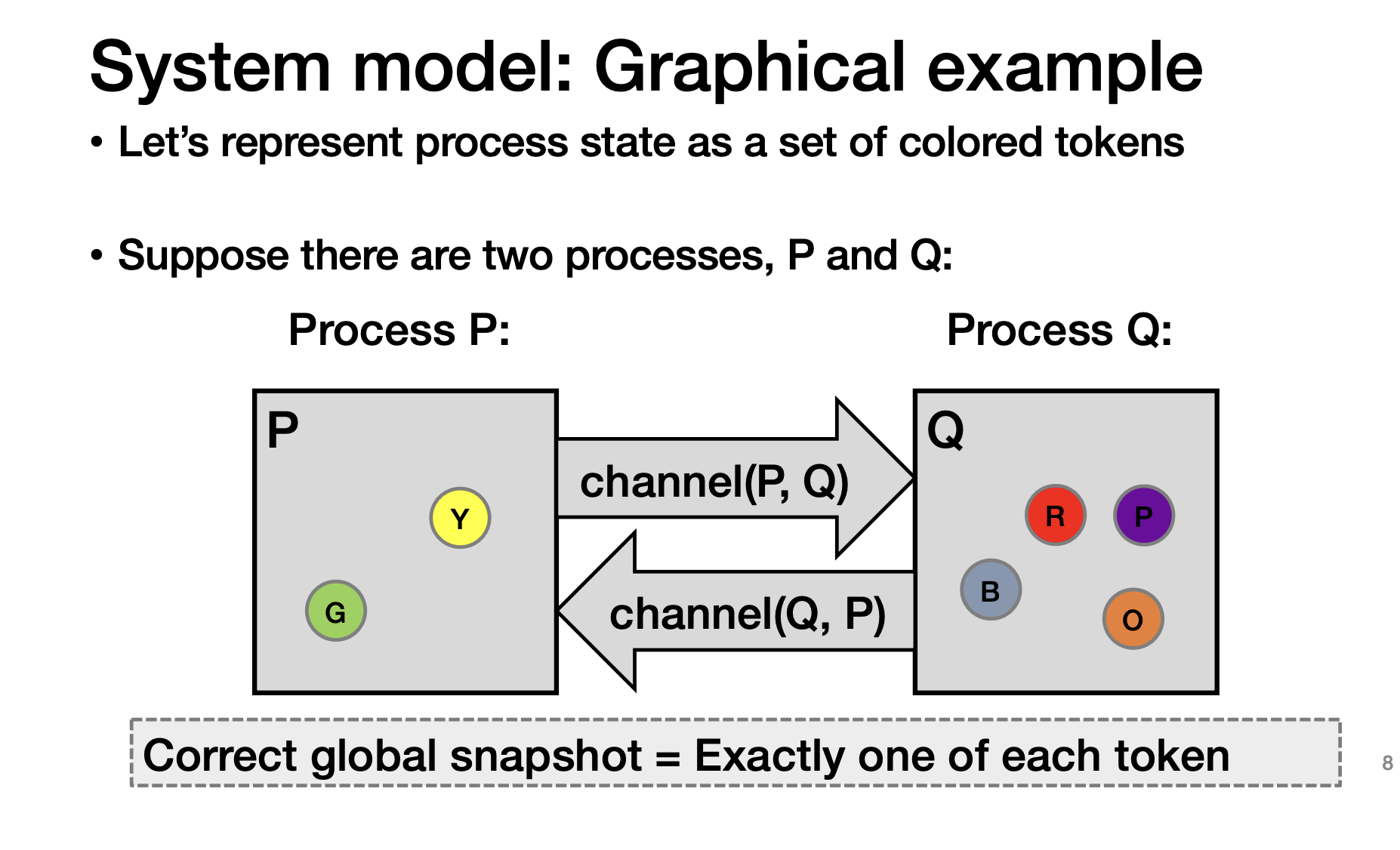
image.png

Design1: 只取两个进程

Problem：那你在通信信道里的数据就丢失了
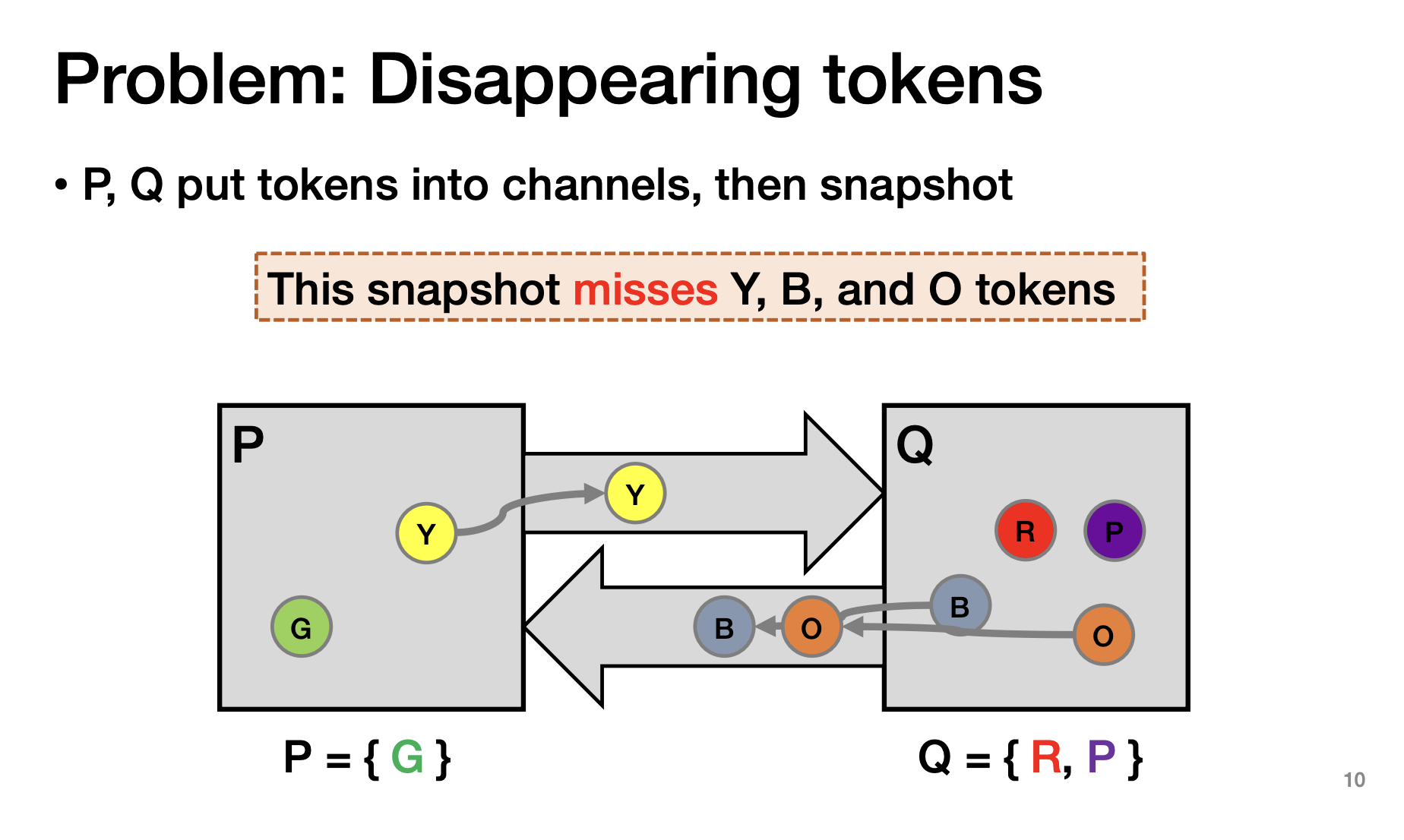
image.png

Design2: P先存，然后发给Q存

问题：可能G还在通信中，你只复制成功了Y，会丢数据或者多数据
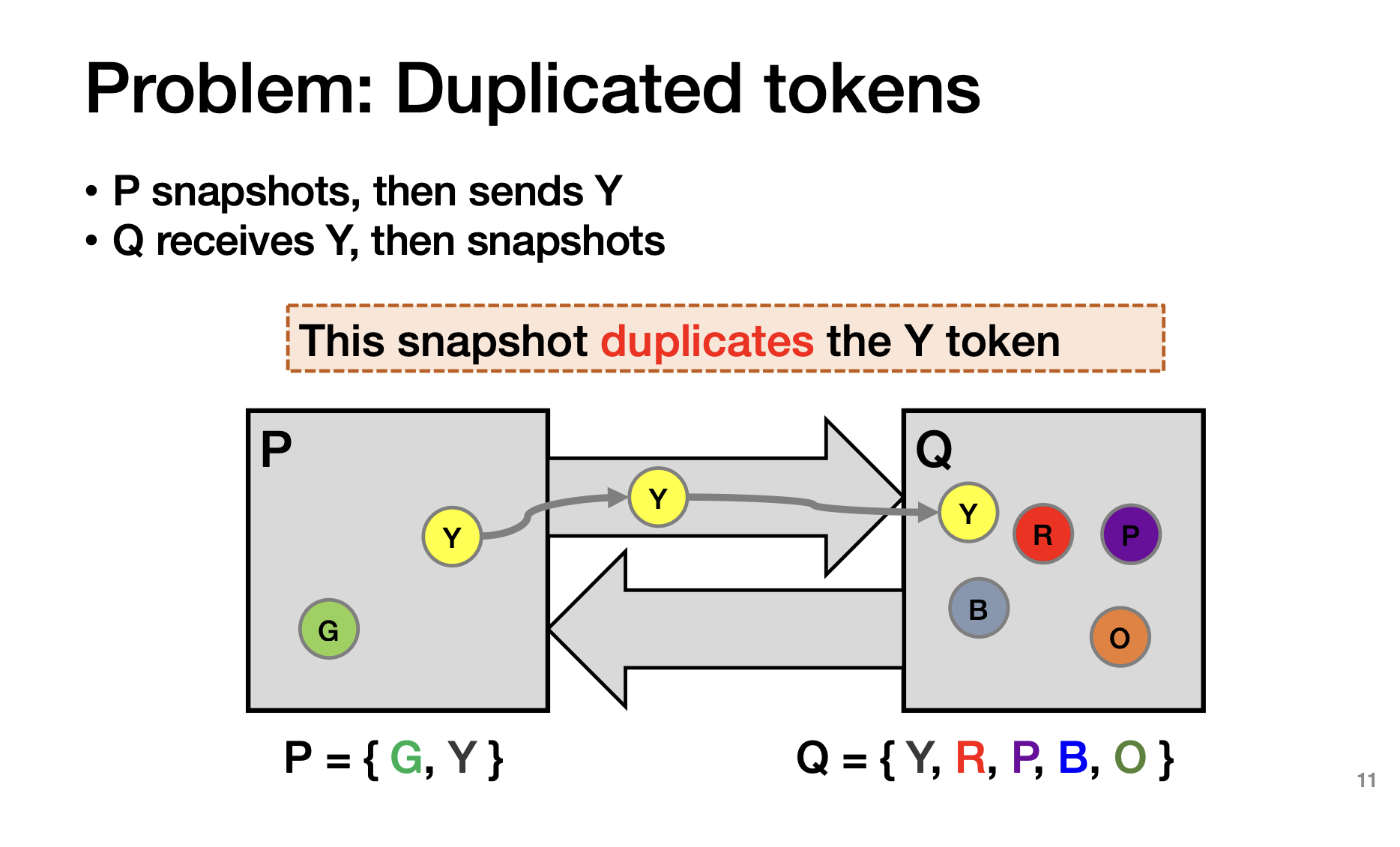
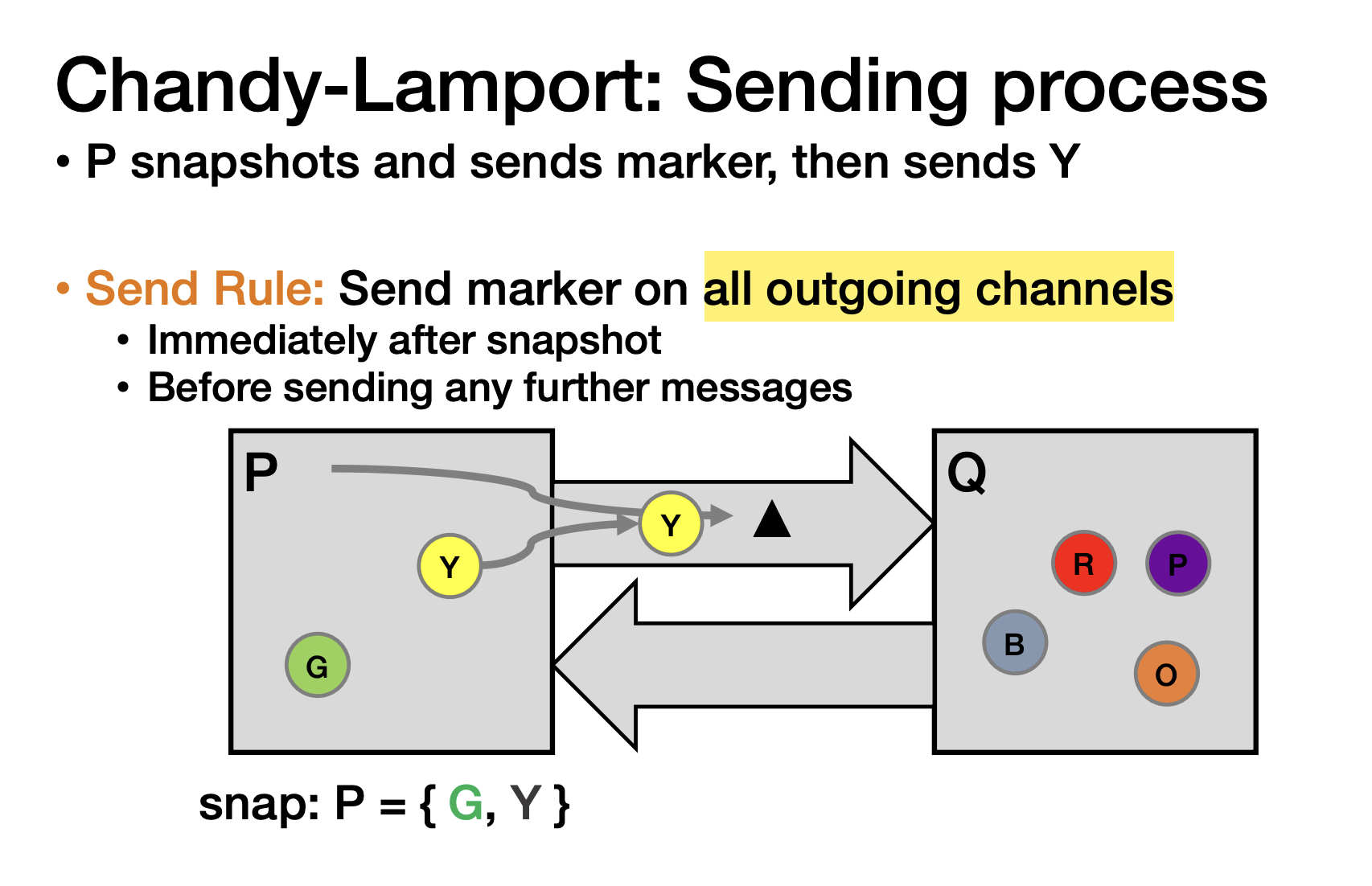
image.png

Idea：设置一个marker消息做同步

这就是Chandy-Lamport Algorithm

image.png

Chandy-Lamport Algorithm

image.png

事件：Q收到 marker，此时又发送O到P

他要做：
把PQ channel 记录为空 （防止记Y造成duplicate）
Snapshot {R, P, B}

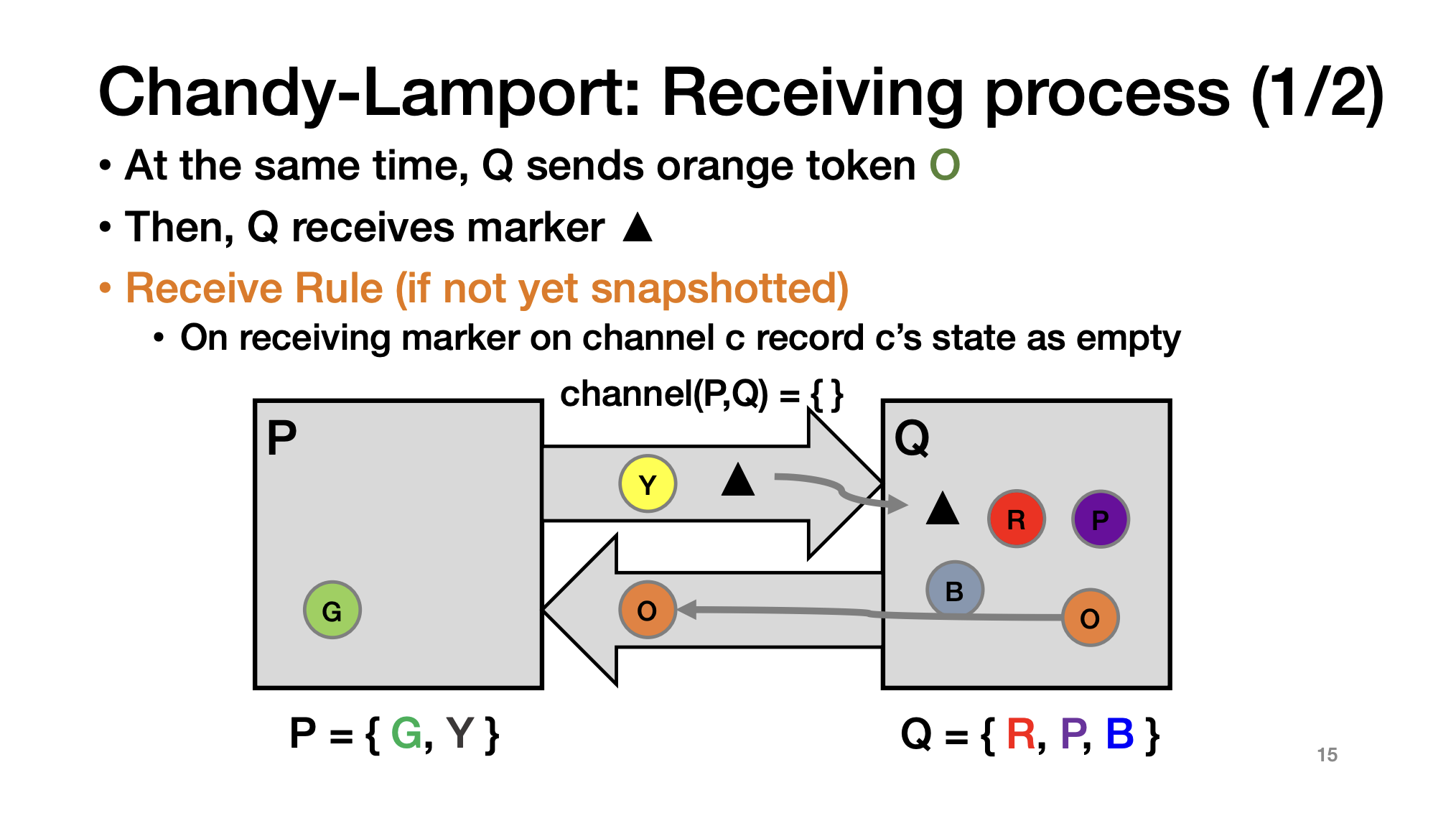
image.png

再发送一次marker，到P后，根据之前的状态，可以同步，确定 channel(Q,P) = {O}
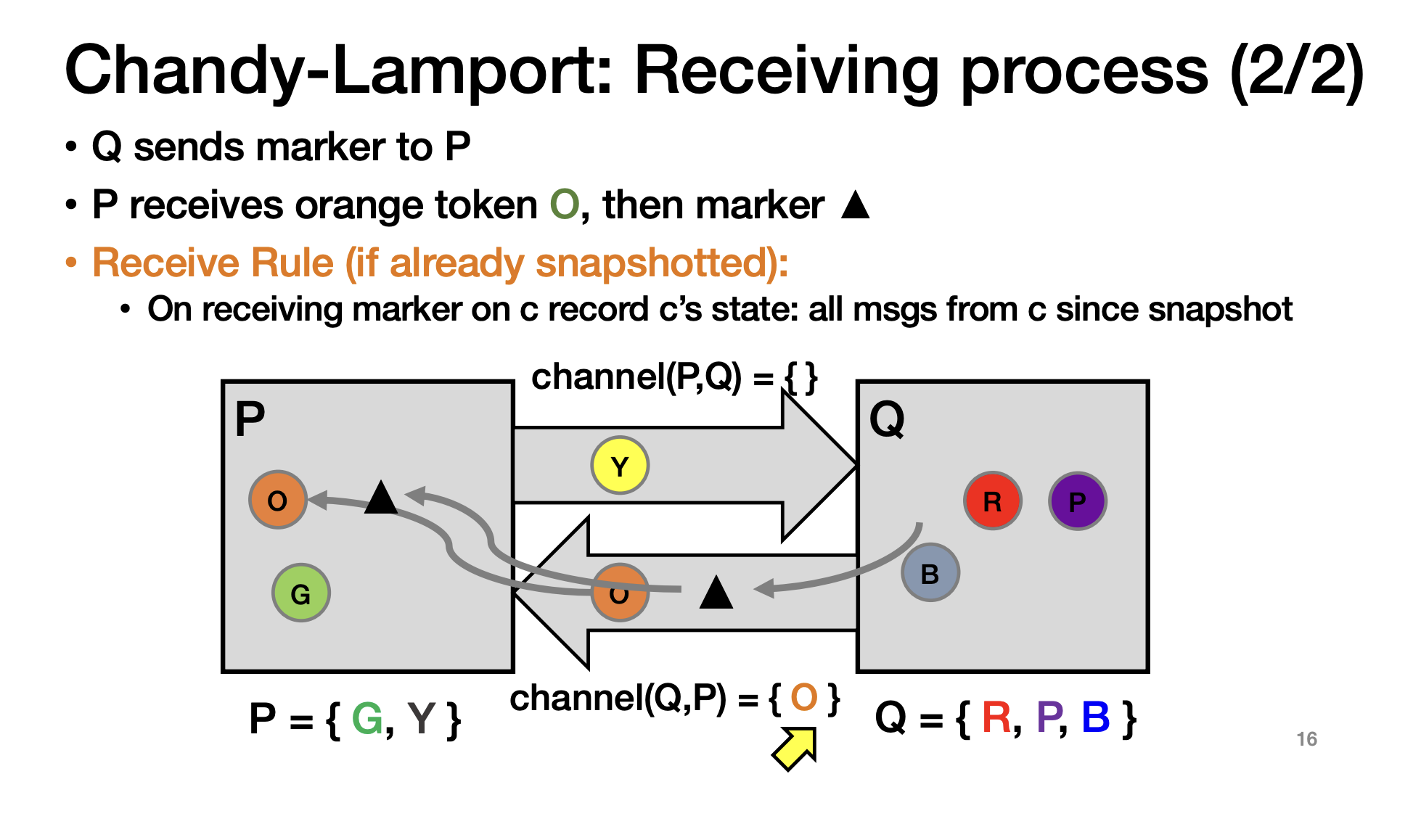
image.png
我们是不用记录同一个准确真实时间的快照，而是记录逻辑意义上的时间

importance: 两个人，只会有一个channel是空的

自己推理下

  1. 发送Y
  2. marker {G}
  3. 发送marker
  4. Q发送B，O
  5. 此时Q应该记录{Y,R,P}，因为之前没记录成功过

1.如果先marker，那么Y一定会在P={Y,G}
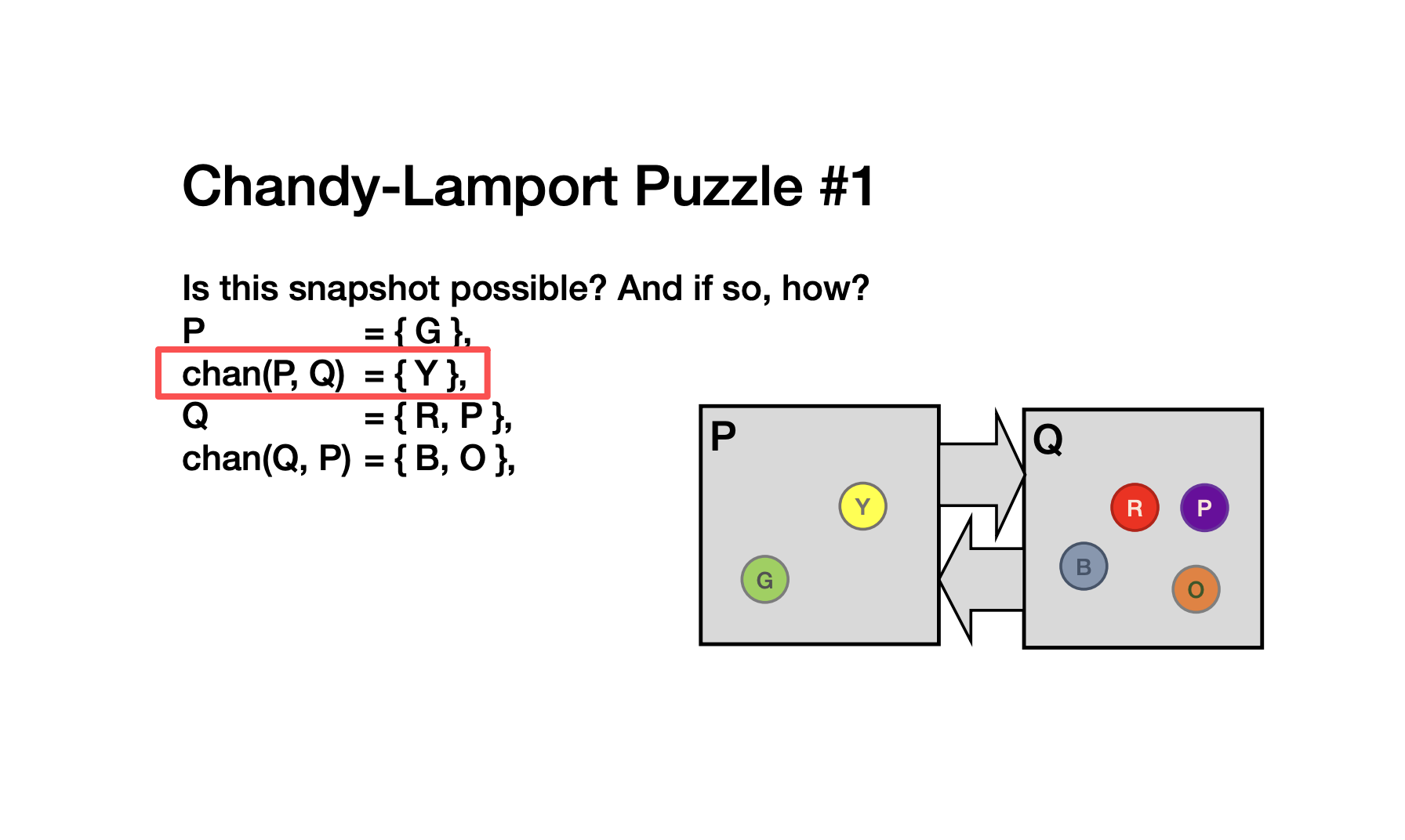
image.png

3个人

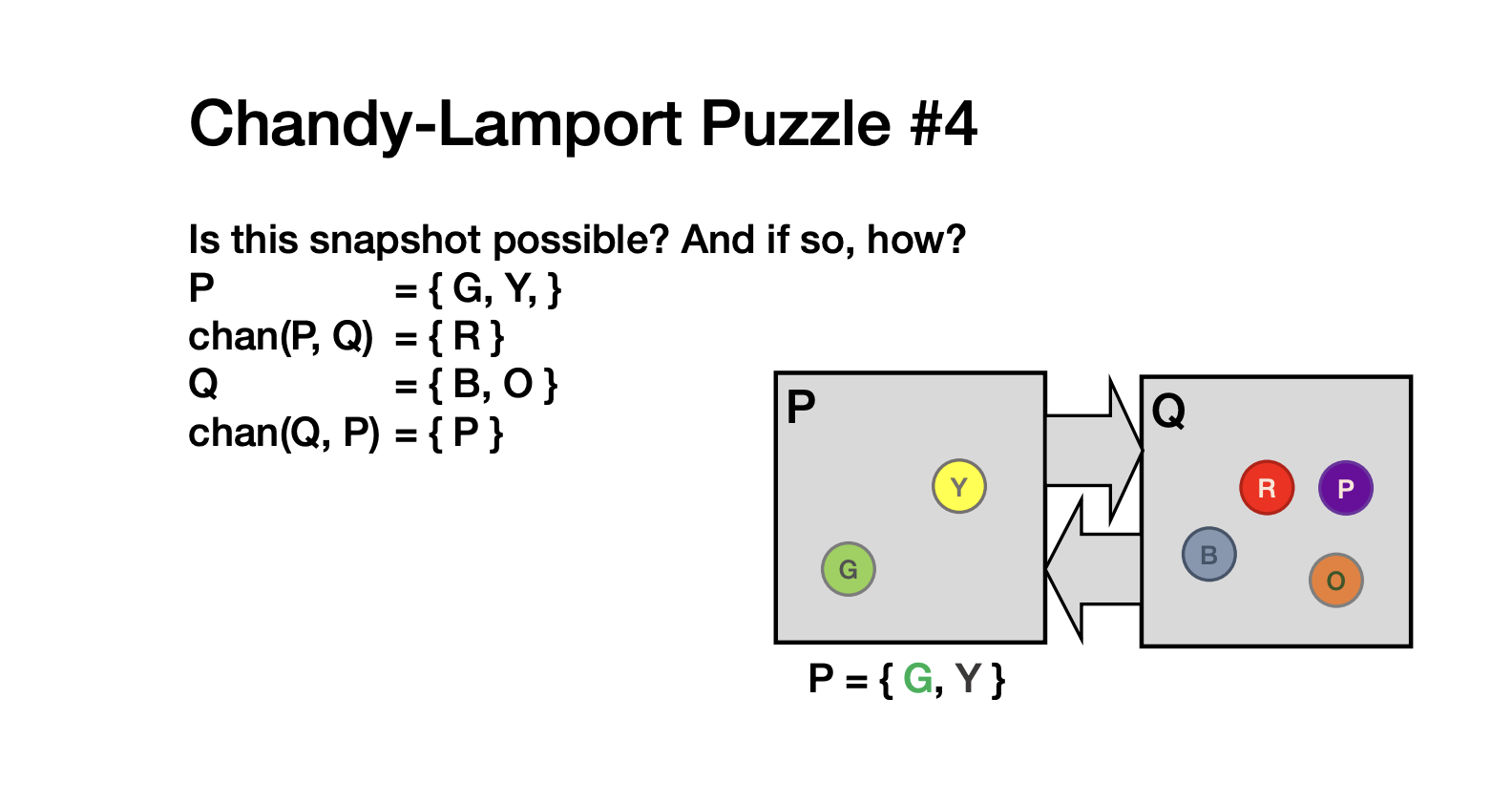
image.png

  1. marker先从T开始 T={}
  2. T发送marker给P，Q。
  3. 在发送途中，P发送R给Q，Q发送P给P
  4. 两个marker并行的到了（同时循序），并且记录，P={G,Y}, Q={B,O}
  5. 此时P和R终于到了，然后marker从P到Q，从Q到P
  6. marker记录，就会得出 chan(P,Q)=R chan(Q,P)=P

如果加两个channel，就可以记录出这个情况
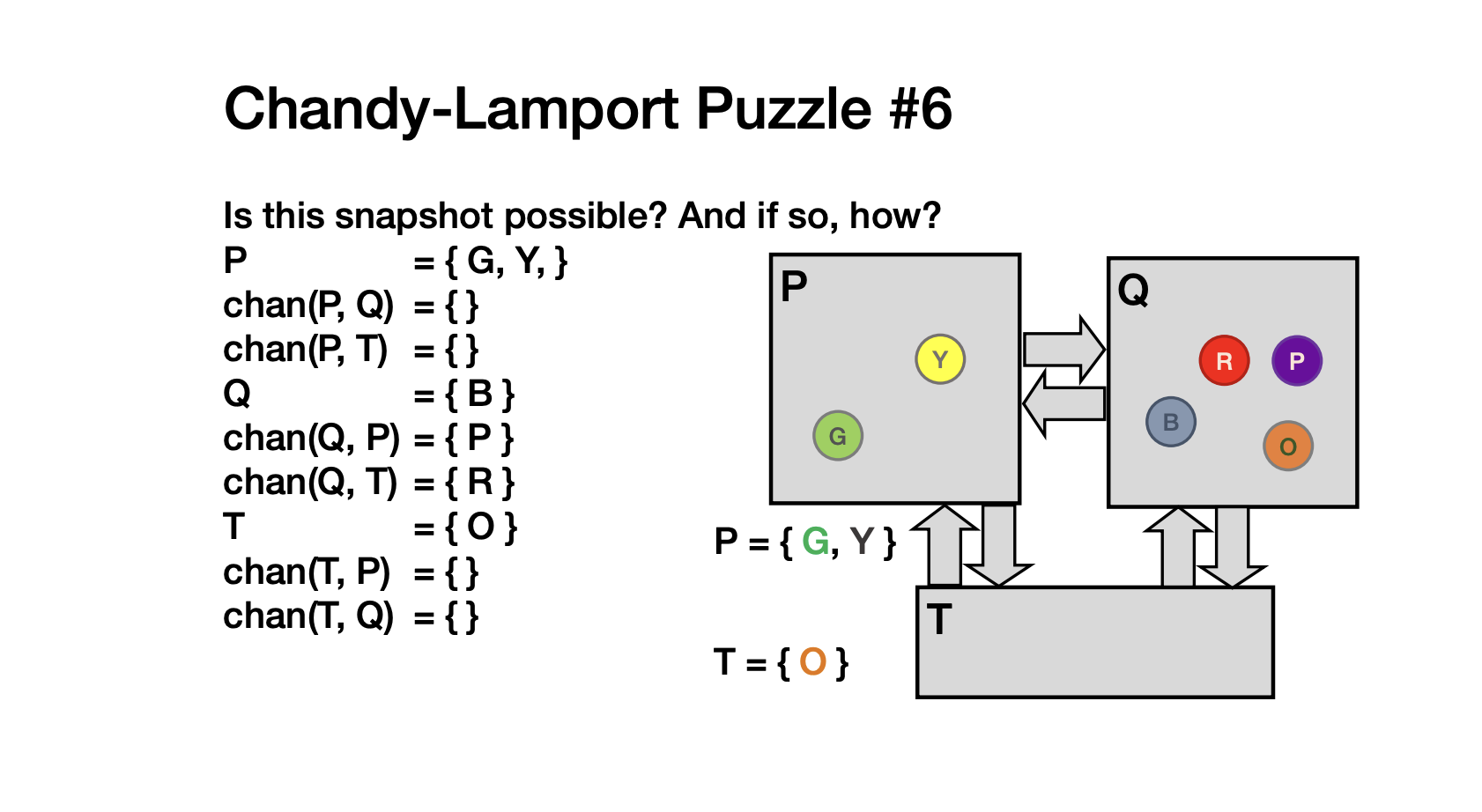
image.png

Chandy-Lamport (1985) 的算法通过一种异步标记协议（marker protocol）解决了上面的两个问题：

  1. 快照启动者发送一个 marker（标记消息）；
  2. 每个节点收到 marker 时：
    • 若是第一次收到 marker → 记录本地状态；
    • 对每条输入通道：
      • 在收到 marker 之前到达的消息属于通道状态；
      • 收到 marker 后的消息属于快照之后的新状态；
    • 然后把 marker 广播出去。

通过这种方式：

  • 不需要全局时钟；
  • 保证每个消息要么属于“已发送未收”的通道状态，要么已被计入接收方状态；
  • 得到的快照是一致的（即不违反因果关系）。
分类 问题 核心原因
理论问题 没有全局时间，无法同步拍照 分布式异步性
状态一致性问题 消息可能被遗漏或重复 发送与接收时刻不匹配
实践问题 网络不可靠、系统规模大 真实系统限制
解决思路 标记协议（marker）、逻辑时钟、差分快照 保证一致性、减少开销

当然在真实世界中：

问题 说明
消息重复 / 丢失 实际网络不是可靠 FIFO 通道，需要额外机制（序号或确认）确保 marker 不丢失
高负载系统的状态膨胀 拍快照可能占用大量内存 / 网络带宽，需要增量快照或差分快照
与应用状态交错 进程状态和通道状态可能不同步，尤其是在多线程或异步 I/O 环境下
一致性与性能权衡 频繁快照会拖慢系统性能；延迟快照则可能增加恢复时间
多快照并发 多个控制器（coordinator）同时触发 snapshot，需区分不同 marker 实例（常用唯一标识符）
非 FIFO 通道 原算法假设 FIFO 通道；若通道乱序，需记录额外因果信息（如 Vector Clock）

快照存储所有事情/过多事情

事情会被Lamport存
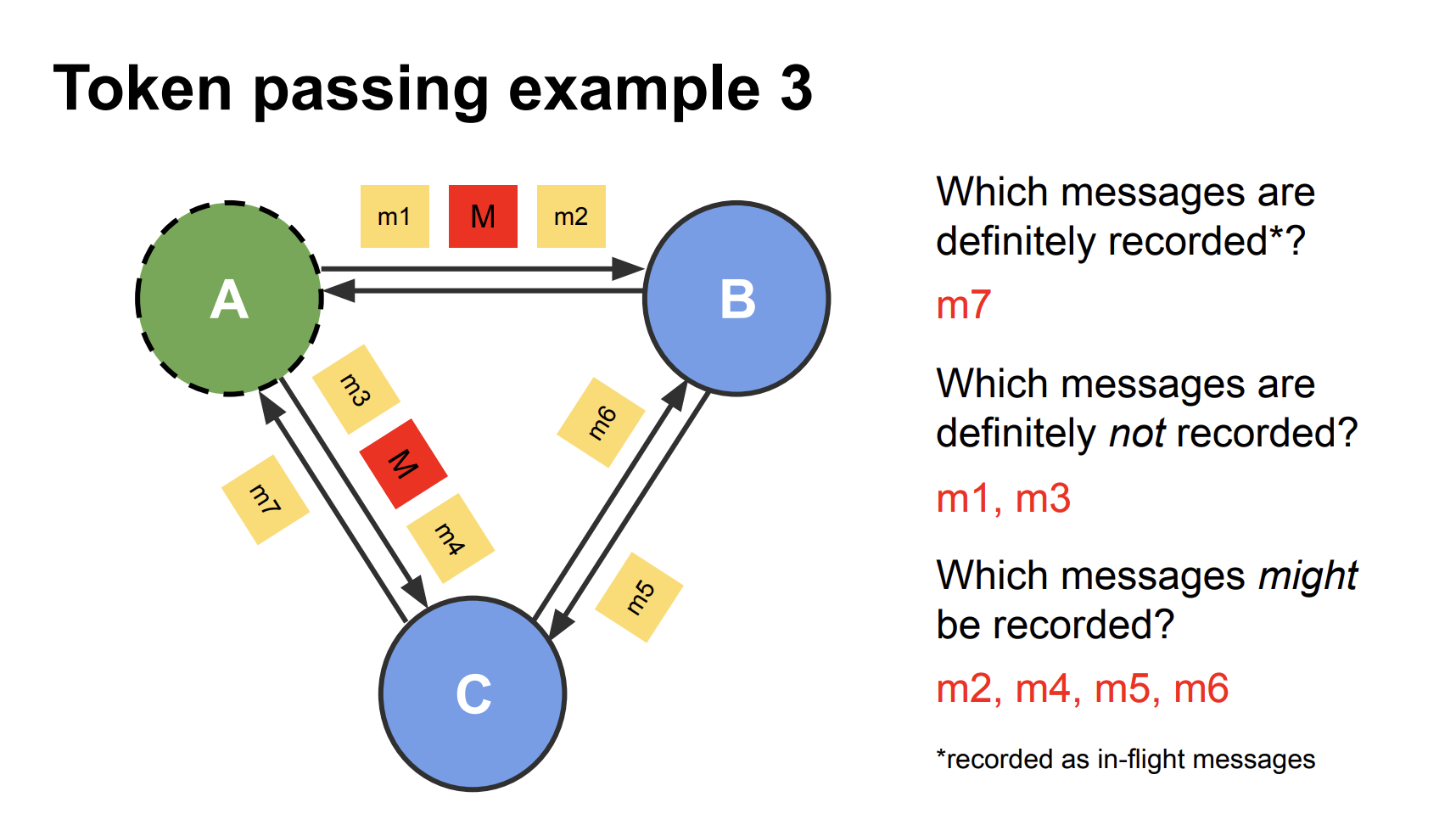
image.png

这个PPT是整个事情的形象版本
https://www.cs.princeton.edu/courses/archive/fall22/cos418/docs/precept_04_distributedsnapshots.pdf