CS205·C/C++ Programming

Project3 Report:  SGEMM Optimization

---

PDF 版本：Project 3
Github: https://github.com/HaibinLai/CS205-CPP-Programing-Project

摘要

在本次Project里我们要优化SGEMM。我们先进行了一些理论探索，然后进行了基准测试。我们对OpenBLAS和Intel MKL进行了测试和底层分析，对其代码结构、指令原理、通信模型进行了研究。这里边无论是不同硬件上的针对优化，还是软件上的分治操作，都是一个复杂的系统工程。而这工程中最重要的一环，便是在“计算-访存”的钢丝绳上保持平衡。我们在这短短的3周内，简单了解工程师们对此的各种思想与工作。

无论是硬件上算力的堆叠，还是软件上循环的优化，GEMM加速带有着计算机独特的暴力美学。让我们跟着这方面的专家，我最喜欢的导演之一，Quentin Tarantino，来导演属于自己的计算程序。

关键词：并行计算；BLAS；向量化；异构计算加速；平衡点理论；SIMD

Part 1: 需求、目标         Chapter 1: Reservoir Dogs

油气湍流模拟、地震波传播演算、分子动力学模拟等科学模拟计算中，通用矩阵乘法GEMM占据了主要的计算过程[6]。图形学、深度学习、大语言模型训练也和矩阵乘法高度相关。本次Project的目标就是优化单精度浮点数通用矩阵乘法SGEMM。

Project3开始的那一周正好去上海打ASC超算比赛了，在比赛里和不同学校的同学交流优化的方案。结果听完他们的优化，我心里只冒出一句话：哎！要是上学期学了C/C++，甚至要是早3个周做这次Project，可能这次比赛，就可以有更多的优化了吧！但是比赛已经过去，明年在场上的可能就是学弟学妹了。所以看到题目的时候，我心里想，一定要做一个比Intel MKL、OpenBLAS还要优秀的GEMM出来，以后学弟学妹们就能用上这个api，让南科大走得更远。

带着这个想法，我针对Project订立了下面几个目标：

1. 熟悉我们的计算硬件；

2. 学习一部分理论知识，应对可能的优化；

3. 测量Intel MKL和OpenBLAS在SGEMM上的性能；

4. 针对不同的矩阵规模，采取不同的优化策略；

5. 测试我们的乘法性能，并试图把它用在科学计算软件中，查看我们程序的加速时间。

Part 2: 平台、决斗场         Chapter 2: FOUR ROOMS

本节介绍我们跟OpenBLAS，Intel MKL比武的场地，CS205 Server和启明38队列。

2.1 CS205 Server              The Misbehavers   

我们的实验与优化将主要在CS205 Server上进行。Server有两个CPU共48核，使用VMware开启虚拟化，使得NUMA node数量为1。配置详见表2.1。同时，该Server也支持sse4,avx2,avx512拓展指令集。

Model name	Intel(R) Xeon(R) Gold 6240 CPU @ 2.60GHz
CPU Architecture	x86_64
CPU family	6
Thread(s) per core	1
CPU(s)	48
Core(s) per socket	24
Memory	128GiB
Caches	100.5MiB
Hypervisor vendor	VMware
NUMA node	1

Server 装备了4张 RTX 2080Ti Turing架构GPU。详见表2.2[12]。

GPU name	NVIDIA GeForce RTX 2080 Ti
GPU amount	4
CUDA Version	12.2
Driver Version	535.171.04
Memory	11264MiB
GPU Base Clock MHz	1350
SM amount per GPU	68

Turing架构是一款比较经典的GPU架构。出于学习的目的，我在这里简单介绍一下Turing架构，比如下面这个72个SM的GPU:

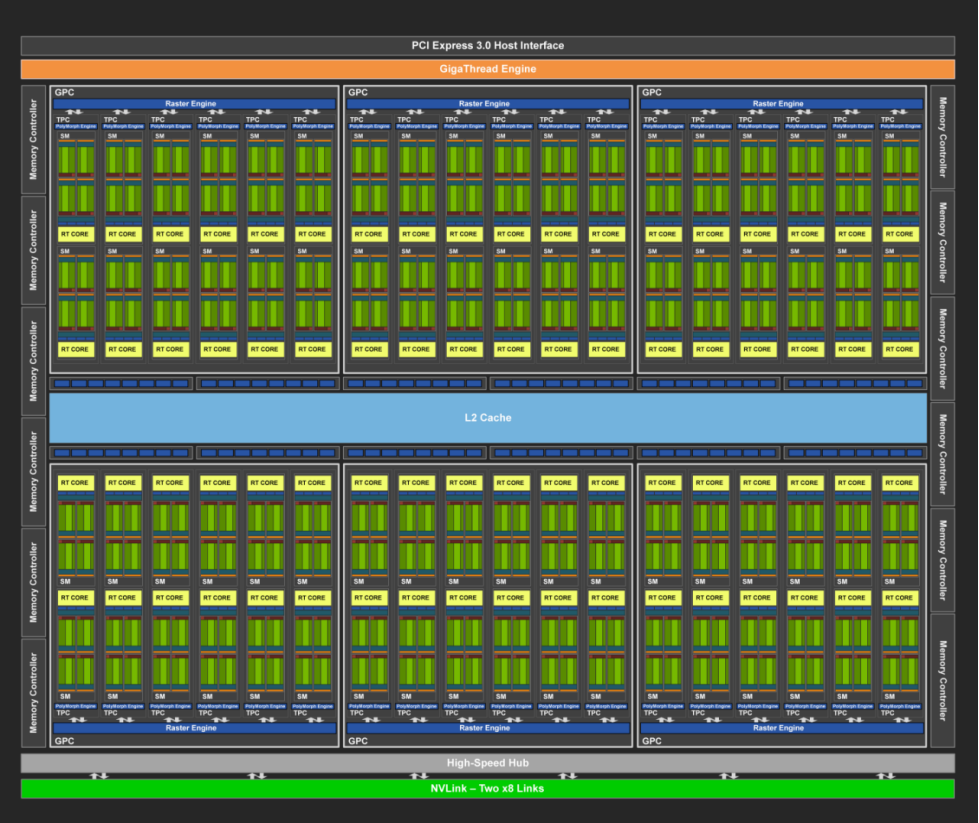
在这里，有这么几个重要的设计理念：

 PCI Express 3.0 Host Interface

 GigaThread Engine

GPC (Graphics Processing Cluster)

Raster Engine

SM (Streaming Multiprocessor)

L2 Cache

PCIe3是GPU连接CPU的沟通线，它会通过链路点对点地与CPU进行全双工通信。GigaThread Engine类似于GPU的OS，但在软件层面再做一个OS，对于游戏渲染还是速度太慢了，因此这个GTE是直接用硬件写出的调度系统。如果GPU是个课题组，你可以认为GTE是课题组的大老板，它会解析PCIe3发过来的各种基金、文章，然后调度小老板图形处理簇GPC开始发文章，创建线程。小老板底下有一个延毕老博士光栅化引擎Raster Engine，这个课题难而且老板关注的不多，所以延毕了。小老板带着一群硕士生TPC纹理处理簇，每个硕士生带着两个做创新实践的本科生SM（Stream Multiprocessor，流多处理器）。

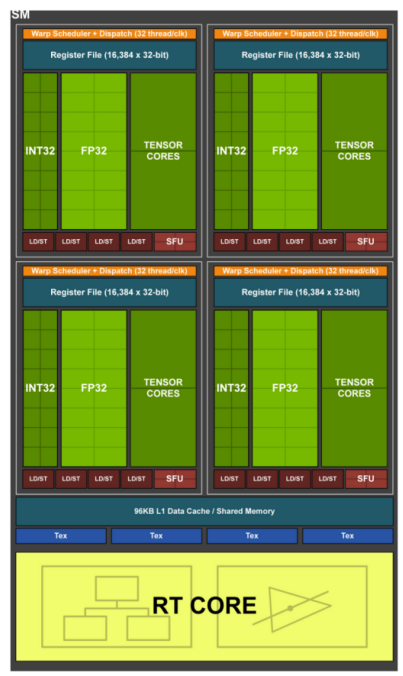
本科生SM就是GPU的帕鲁，他们负责执行具体的运算，SM里有很多个CUDA Core，比如整数运算Core，浮点数运算Core，张量tensor Core，Turing架构特有的光线追踪RT Core（本次Project可能很难用到它），特别函数SFU Core。他们每个都有自己的小ALU，SM会通过4个Warp Scheduler来分别调度使用他们，Dispatch会给Core们分发具体的指令与数据。

Warp是一个很可怕的驱动者，它就像GPA，会尽可能地压榨学生的Core。比如它收到1个命令要开启32个线程计算浮点运算，那它就会要求16个FP Core一起计算2次。这样的计算模型被叫做SIMT，单指令多线程。如果在计算的过程中出现了分支问题，Warp会继续从Instruction Cache中取新的指令，让这群Core永远都不能躺在宿舍里睡觉。

1个Warp Scheduler内的核心计算出的结果会存储在register File中，而SM内要想Core执行的线程实现相互通信，就要借助SM的L1 Data Cache，这样，一个SM内通信就建立起来了。而如果本科生想跟组内其他人交流，就要通过组内大群/飞书：L2 Cache来进行通信。

而如果一个GPU课题组想跟另一个课题组合作，传统的方法是GPU通过PCIe3将数据发回到CPU的DRAM Main Memory上，另一个GPU再去拿取数据。更先进的方法是NVLink，它通过高速通道直接与别的课题组建立合作通讯。

2.2 启明超算集群38队列               

在本次Project中我将自己的GEMM算法应用到实际的软件中，并使用南科大科学与工程计算中心启明超算集群38队列进行标准测量。

截至2024年2月，南科大“启明”超算集群拥有299个计算节点，10072个计算核心，每年可向用户提供超过8823万核时计算资源，支撑着13个院系116个课题组的科研计算需求。而其中属于“启明2.0”的38队列是启明集群内使用率最高的队列，课题组用户用量大。针对该队列的算法优化可以帮助减少用户作业的计算时间，提高队列计算效率[25]。

38队列共有36个刀片节点。每个节点CPU型号为Intel Xeon(R) Gold 6338 CPU，单节点内有2个NUMA node，64核，50MB Cache及512GB Memory，CPU支持sse4,avx2,avx512拓展指令集。节点间使用200GB HDR Infiniband Switch进行通信，作业采用IBM Spectrum LSF调度系统进行管理[24]。

2.3 平台软件              

在CS205 Server上老师提供了gcc, nvcc编译器，make和cmake工具以及nsight性能检测器。我在此基础上又编译了OpenBLAS数学库, OpenMPI以及下载了Intel® oneAPI Base Toolkit，内含Intel MKL数学库和Intel MPI，Intel VTune Profiler。

在启明上集群使用module管理工具对软件进行管理。上面提供了gcc，make和cmake，在此基础上我也安装了Intel® oneAPI Base Toolkit。下表为平台数学库、编译器与操作系统具体版本。

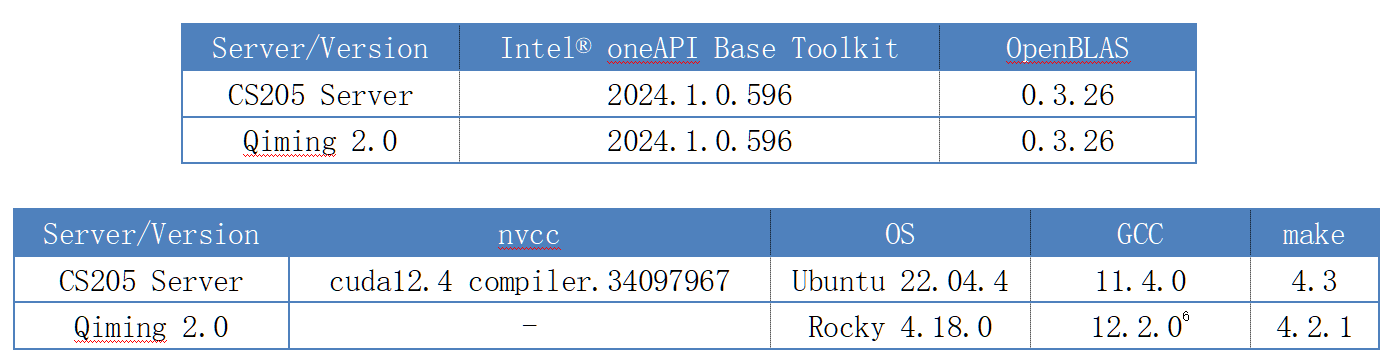
Part 3: 标准、规则、赛场     Chapter 3: PULP FICTION

要击败我们的对手，我们在选定好比武的场地后，要定下比武的规则，和提升武力的法则，另外，在赛场准备时，仔细观察我们的对手。

3.1 时间测量                             

我们将测量我们的乘法计算运行时间。为此我们使用High-Performance Linpack Benchmark（HPL）中计算使用时间的函数HPL_timer_walltime。其使用<sys/time.h>和<sys/resource.h>获取系统时间。

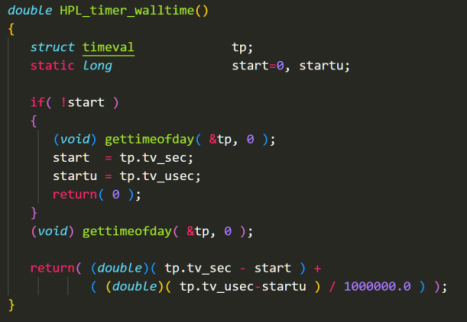
计算机在计算矩阵乘法时，会受到许多相互独立的随机因素的影响，比如此时计算机的温度，瞬时时钟频率，当前要计算的浮点数数值等等。相对整体计算而言每个因素变动较小，所产生的影响也较小。我们可以近似地认为在计算系统未受到大干扰（如CPU核已全部被占用、程序被人为杀死）情况下，根据中心极限定理，程序执行所用时间服从正态分布。因而对于每组数据我们进行多次测试，排除时间在 2 sigma 的情况，取5次数据的平均值作为当前输入情况下的测量结果。

3.3 借鉴GEMM乘法api 与 矩阵Structure设计    

我们的乘法优化算是SGEMM优化的一部分。它是BLAS(Basic Linear Algebra Subprograms，基础线性代数程序集)中Level3的一个重要子程序。要想更好地达到我们Project的目标，我认为我就应该看看它到底是什么，至少应该看看我们的对手OpenBLAS长什么样子，然后再定下标准api和优化的方向。

在BLAS库中，线性代数的计算被分为了3个Level,level1支持向量间的操作，如交换，点乘；level2支持向量与矩阵之间的操作，level3支持矩阵与矩阵之间的操作，GEMM就是里边的重要函数，用的最多的就是SGEMM和DGEMM[26]。GEMM表示下面这样一种标准运算：

C\gets \alpha AB+\beta C\ ...\left( 3.2.1 \right)

从文章[26]查找GEMM的输入，一共有这么几个输入参数，下面进行一一解释。

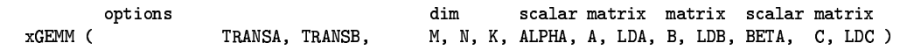
Parameter	Explain
CBLAS_ORDER	是行主序还是列主序完成
TRANSA:	矩阵A是否转置
TRANSB:	矩阵B是否转置
M	A的行，C的行
N	A的列，B的行
K	B的列，C的列
ALPHA	公式3.2.1中的alpha，单纯的乘法取1
A	矩阵A
LDA	矩阵A的leading dimension
B	矩阵B
LDB	矩阵B的leading dimension
BETA	公式3.2.1中的beta，单纯的乘法取0
C	矩阵C
LDC	矩阵C的leading dimension

(注意这里的MNK都是A，B转置后的数 参考：https://blog.csdn.net/yutianzuijin/article/details/90411622)

我们也在函数的实现中加入这些输入的参数，但是我们不会亲手实现里边的每一个参数所需的函数。他们有的不太会在Server中的测试用到，我不会也不可能在两周内给老师交一个手搓的BLAS出来，这是Jack Dongarra的课题，更别提超过现有的MKL。但是我可以借鉴OpenBLAS的代码结构和输入参数，在更好地实现我们自己的矩阵乘法的同时做出一个接口，方便以后拓展，在优化程序上使用到。

我们去查看OpenBLAS的源代码( https://blog.csdn.net/xqch1983/article/details/137585755)，会发现OpenBLAS是这样做矩阵乘法的：

BLAS的底层分为3层，接口层，驱动层，以及核心层。

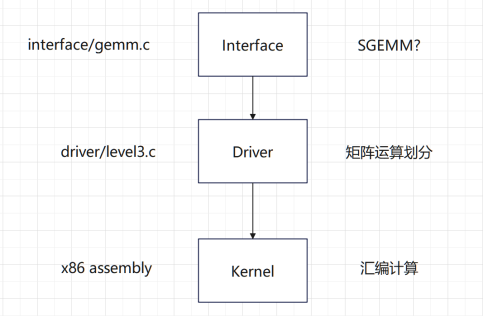
BLAS在接收到SGEMM()输入的参数后，首先会进入Interface层。在这里BLAS会对输入的参数进行解析，决定选择不同的算法和分支。如下图（1）是gemm.c中的一段判断矩阵是否转置的部分，随后会根据转置的情况来调用具体执行计算的Driver。

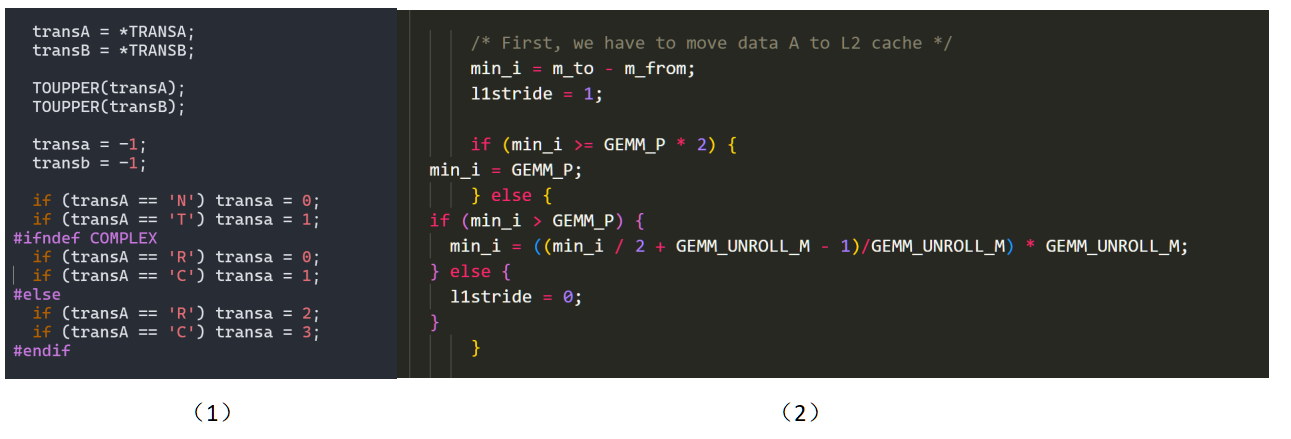
在Driver层数据会被预处理和存储，任务会被分配到各个CPU上。例如如果有转置，数据会被提前处理；CPU会接收不同的任务准备并行处理；缓存会被提前分配，如图（2）。在一切准备就绪后，BLAS会进入Kernel层。

Kernel层占运算的主要部分，为了达到最极致的优化，OpenBLAS用了多种方法：1.针对小矩阵专门设立小型函数（图3左侧small_kernel）；2.在x86_64平台使用AVX512指令集（图3右侧）；3.面对特殊的输入矩阵采用循环展开（图4），根据Project2的效果，这样可以减少执行的汇编指令；4.不演了！直接使用汇编代码来进行运算（图5）。

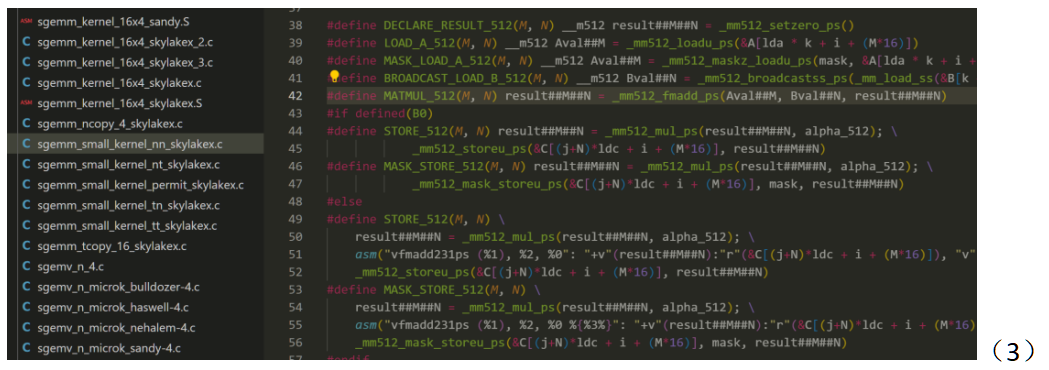
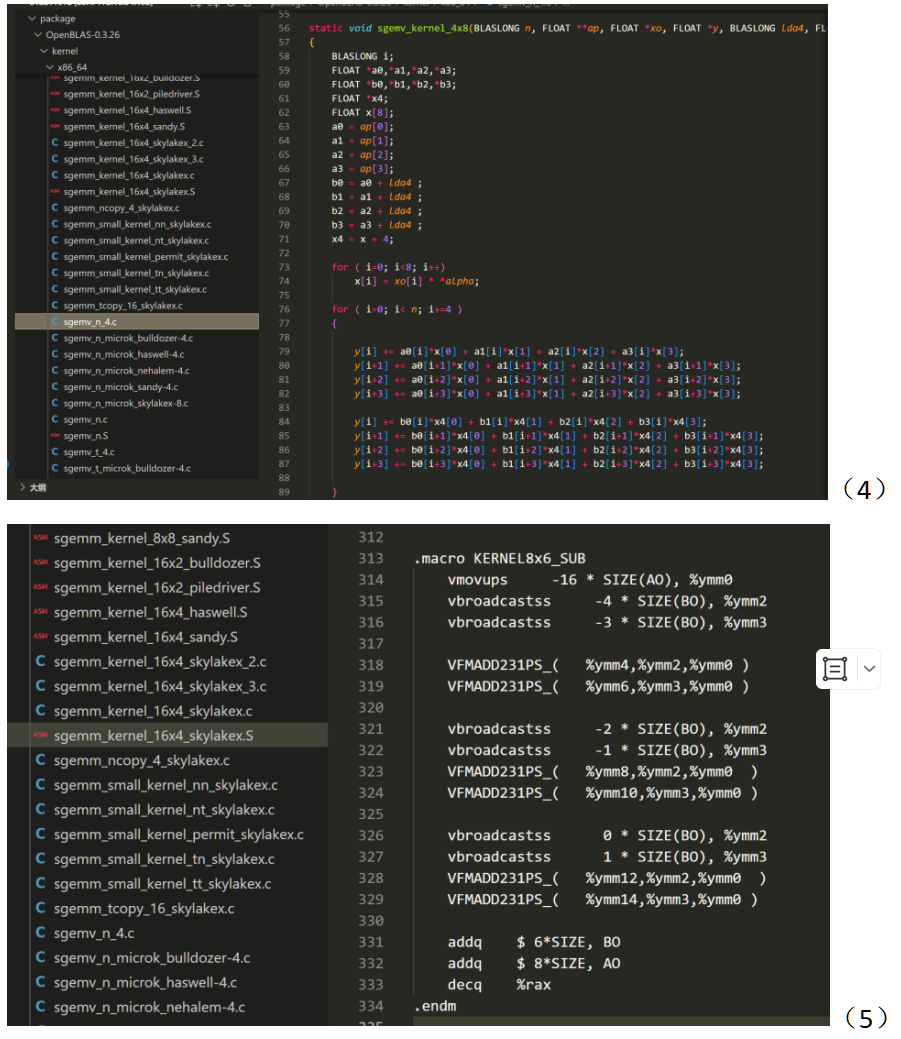
在固定了MNK后，对循环结构进行循环展开是一个很经典的ijk乘法优化方法。在Project2的工作中我们知道，ijk循环在O3选项下被编译为使用寄存器存储ijk的汇编语言，而展开可以减少这一汇编语言的使用，从而降低循环时间。

讲了那么多，我设计了自己的小GEMM BLAS，俗称GBLAS：

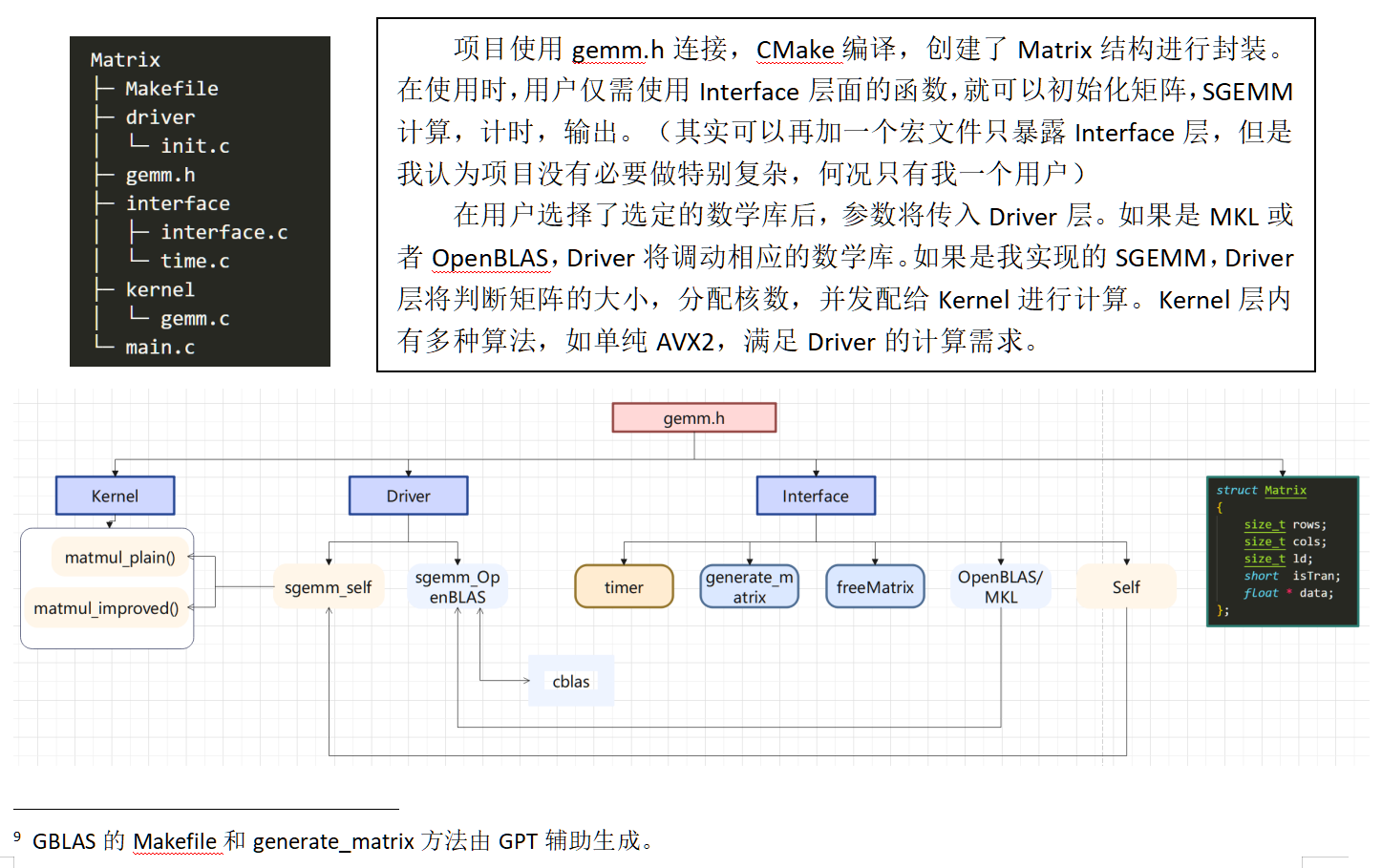
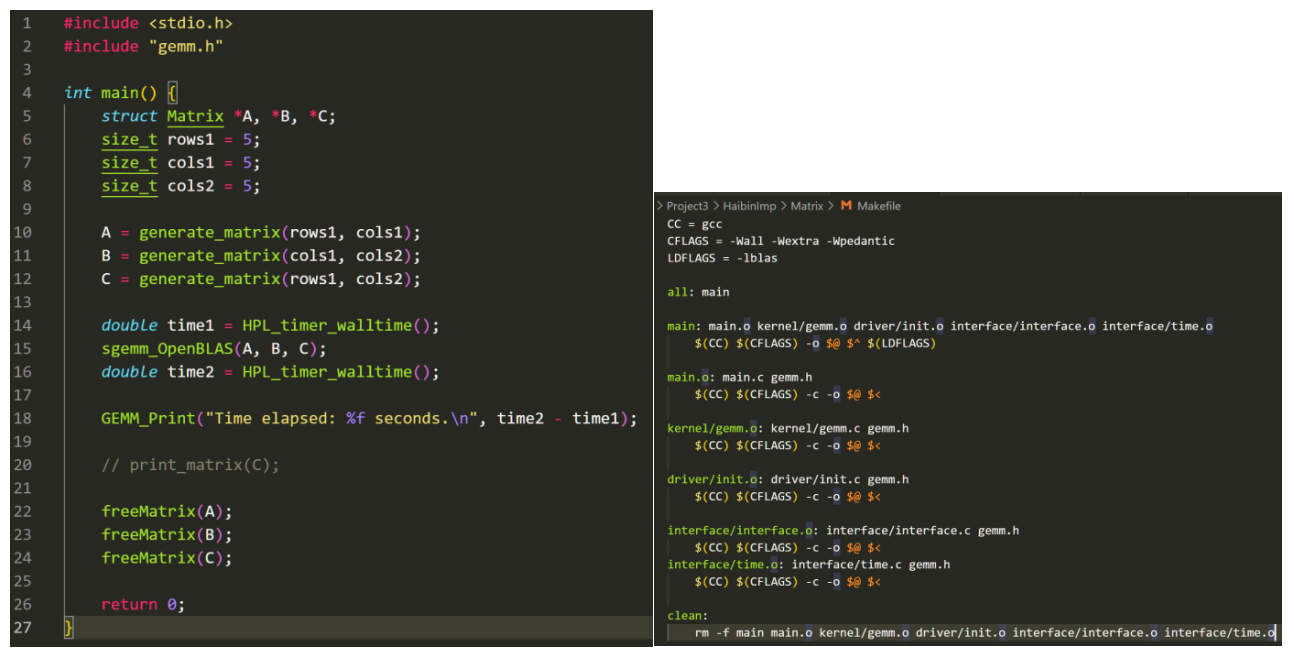
我们的main函数看起来还算整洁，可以满足Project。且通过封装我们可以给矩阵管理是否转置等操作。

在写生成矩阵时，我发现使用malloc函数会出现问题：在问题规模到60K x 60K左右时，malloc会撞上已分配的内存，从而导致segment fault。GPT给了方法是使用linux mmap函数。这个函数会在在当前进程的虚拟地址空间中，寻找一段空闲的满足要求的连续的虚拟地址，跳过已经分配的内存，建立起一个新的“虚拟”映射。不过这样的虚拟化跟malloc相比也带来一定的性能损失。不过这对我们加速矩阵乘法影响不大。（对mmap不错的介绍：https://zhuanlan.zhihu.com/p/691717824）

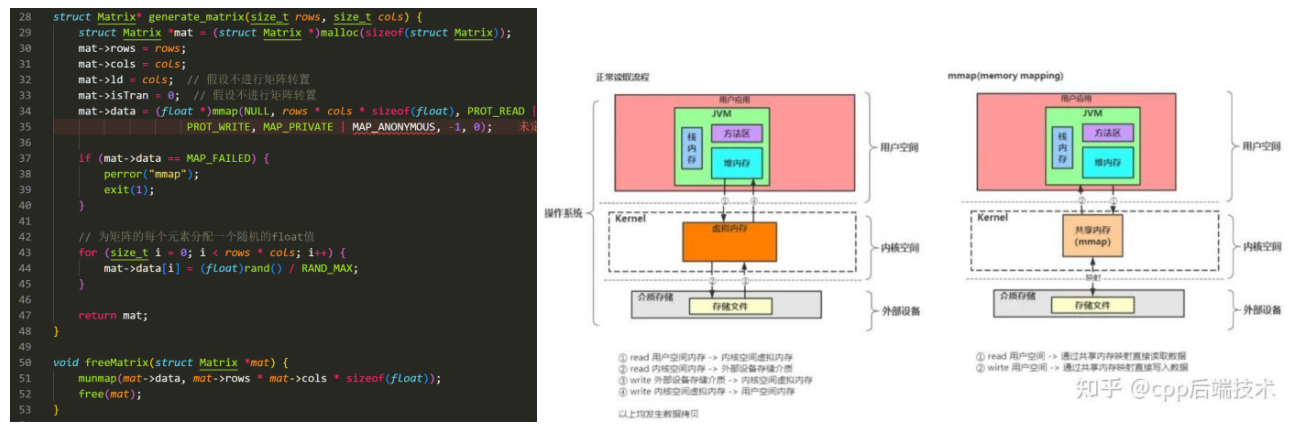
3.3 计算-通信平衡公式

在整场决斗中，我们在单核内要尽可能地减少指令，把数据尽可能地往Cache放。而在多核上在并行算力增加的同时，考虑通信的成本。这是一个复杂的系统优化工程，而我们有下面几个分析工具：

1. Parallel Computing

Amdahl's Law: 这个公式帮助我们衡量我们的并行提升的有效能力。

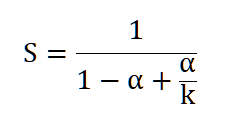
计算机体系结构 量化研究方法 https://zhuanlan.zhihu.com/p/675410026

2. CPU

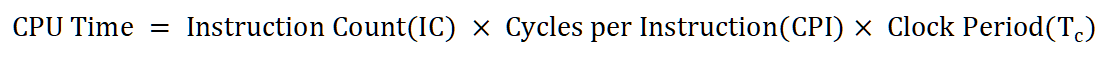
3. Cache

Cache Rule：

大小为N的直接相联和大小为N/2的2路组相联的缺失率差不多。

Hit Probability in Cache**[27]**:

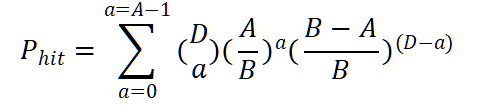
展示了一块有A associativity, B block的Cache, 在栈距离D的情况下缓存命中的概率。

Effective Access Time:

 具体的公式推导可看论文[27]的附录。

4. GPU

GPU浮点运算理论峰值Peak FLOPS:

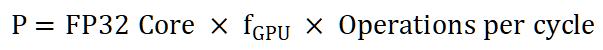
Part 4: SGEMM测试与观察      Chapter 4: THE HATEFUL EIGHT

BLAS测试

本节我们将进行标准ijk，OpenBLAS，Intel MKL针对不同大小的单精度浮点数矩阵的计算时间测试。我们将不同的参数输入到矩阵中，得到基准测试的结果。同时，我们会观察对手的招式：使用核数，分解动作等等。

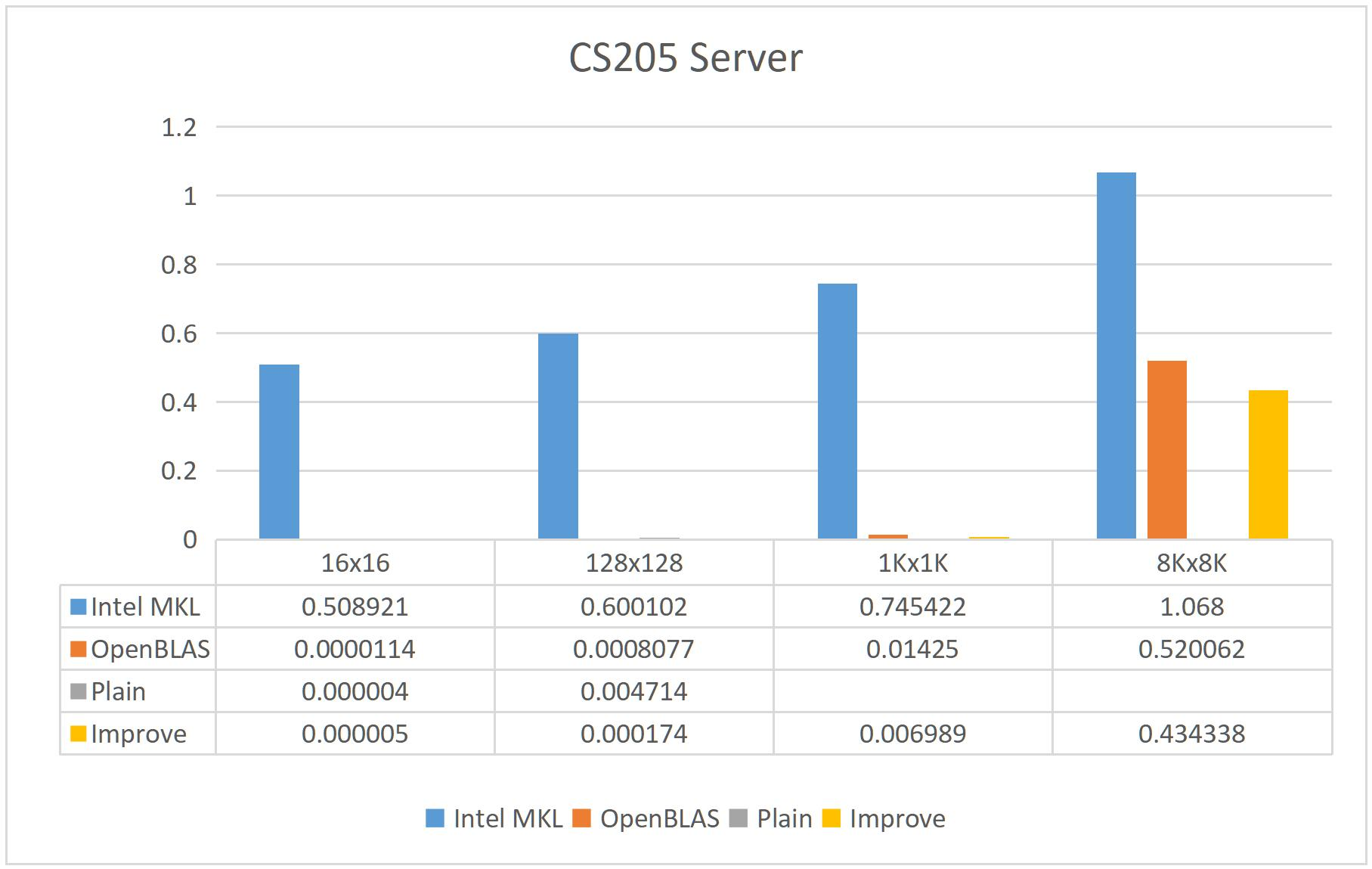
我们首先看看Server的情况。Server上受到了非常多的干扰，许多次程序都无法正常运行，在64K x 64K，40K x 40K上都没有收集到完整数据。再加上老师说过高耗时的程序就不再分析，于是我仅列出下面5种矩阵规模中的部分情况。为了使数据方便展示，对条形图进行了底数为10的取对数操作。（原始单位为秒）

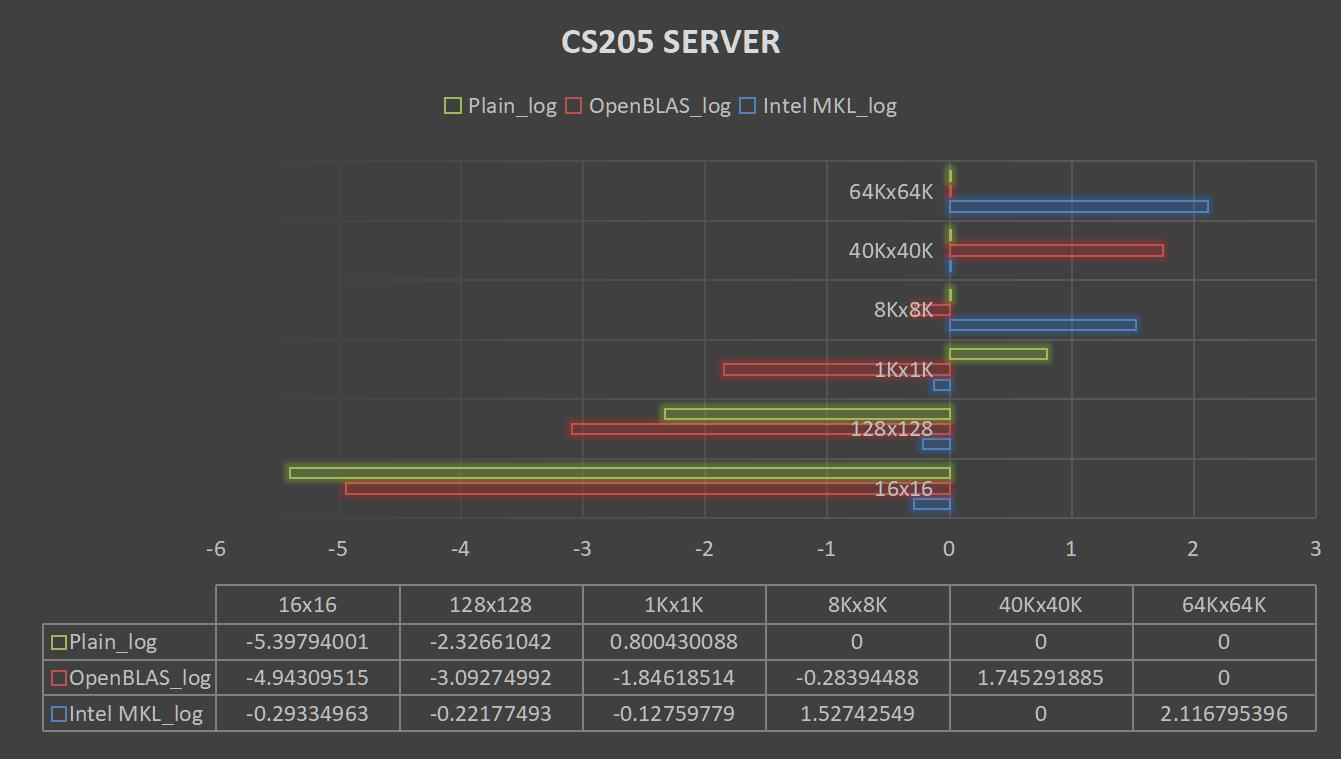
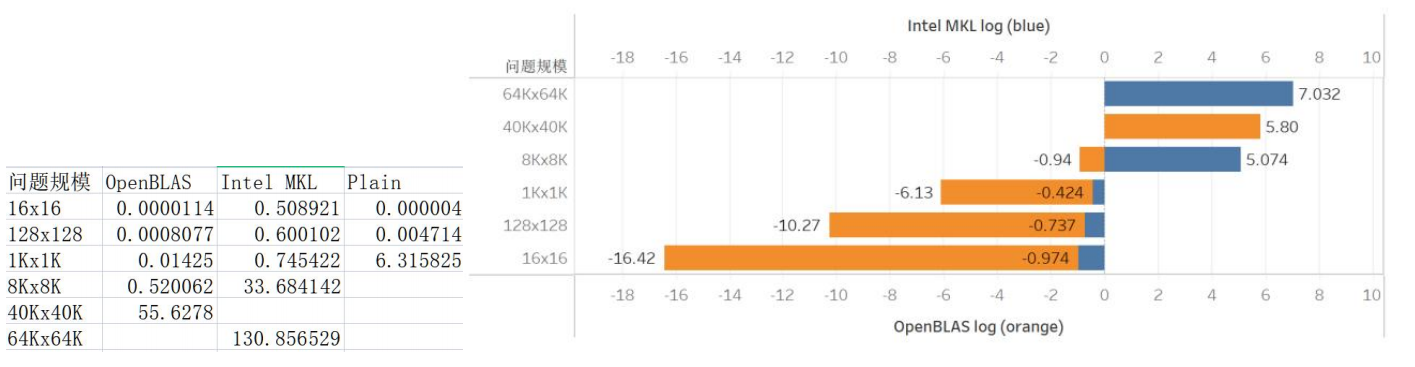
之后我也在启明上进行了测试：

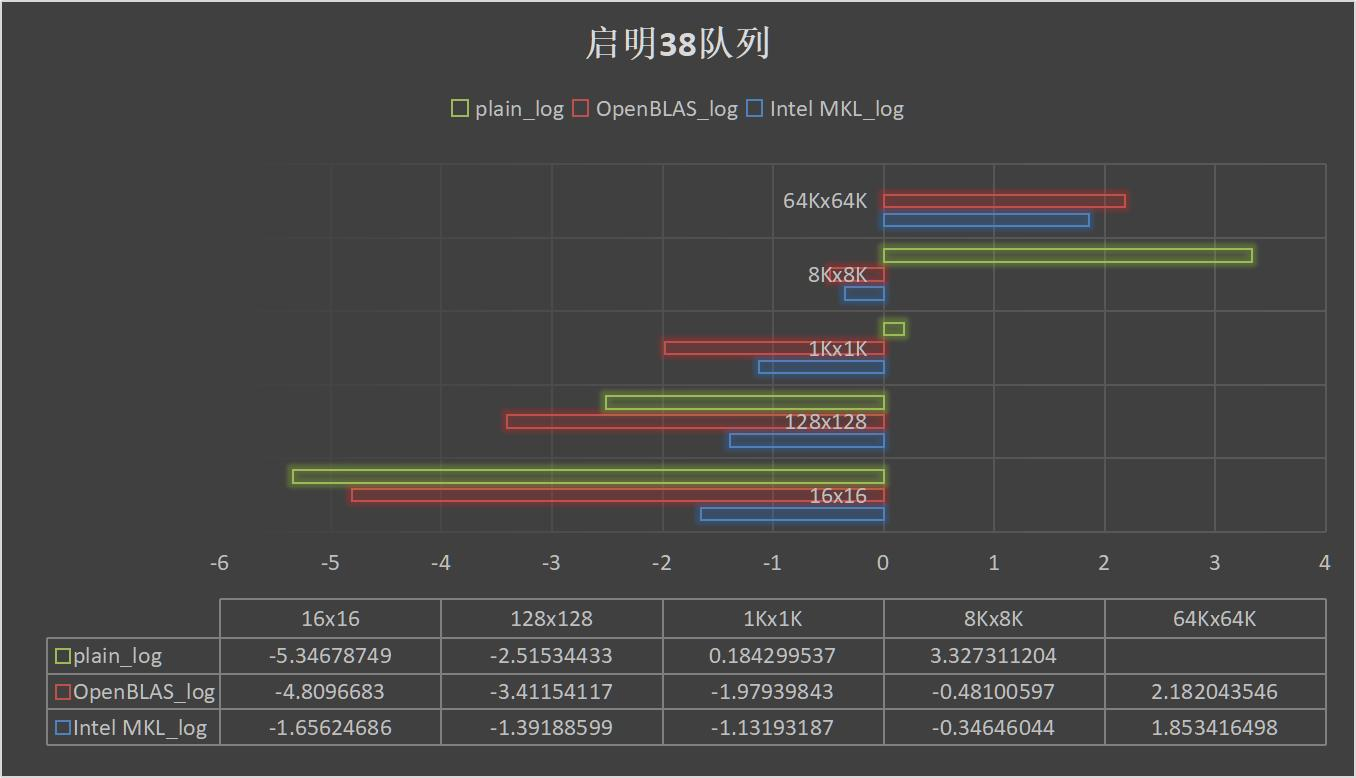
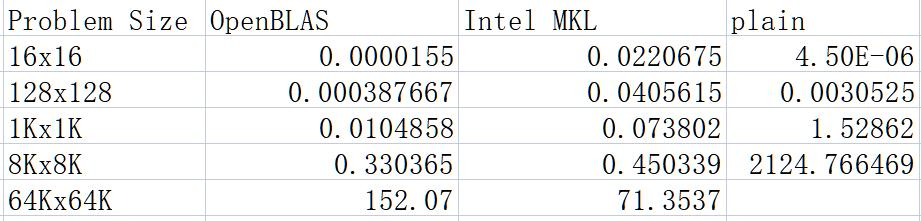
在启明上的数据相对干扰不大，我们也可以看到三种实现方法的区别。在小数据内，直接采用plain方法是最快的，这是因为OpenBLAS和MKL还在传参时，Plain方法就基本上算完了矩阵。但是很快中型数据规模下OpenBLAS占据了主导。从汇编代码分析，这应是因为OpenBLAS在小数据规模的矩阵乘法上做出了许多优化，而Intel并没有特别聚焦这部分的内容，从文章[15]可以看出，他们居然在用JIT做小矩阵的优化，它会将我们写的部分代码转换AVX2或者AVX512，对不同的CPU型号采用不同的OpenMP线程，不同的策略。它的规模是小于16和128的矩阵。但是很不幸，这样的优化似乎OpenBLAS做的更好......（可能只是他们的员工留下了优化的空间，这样以后自己就不会被过早优化了）

但是MKL在大矩阵的计算上超越了OpenBLAS。在64K x 64K上领先对手一倍的速度。根据以前学长的测试，大矩阵的优化都是MKL较佳，在跑HPL时也是统一用的Intel MKL。不过MKL是怎么做到的？我决定来分析一下。于是首先请出我们的老朋友VTune。

我们对Intel MKL和OpenBLAS分别进行分析:

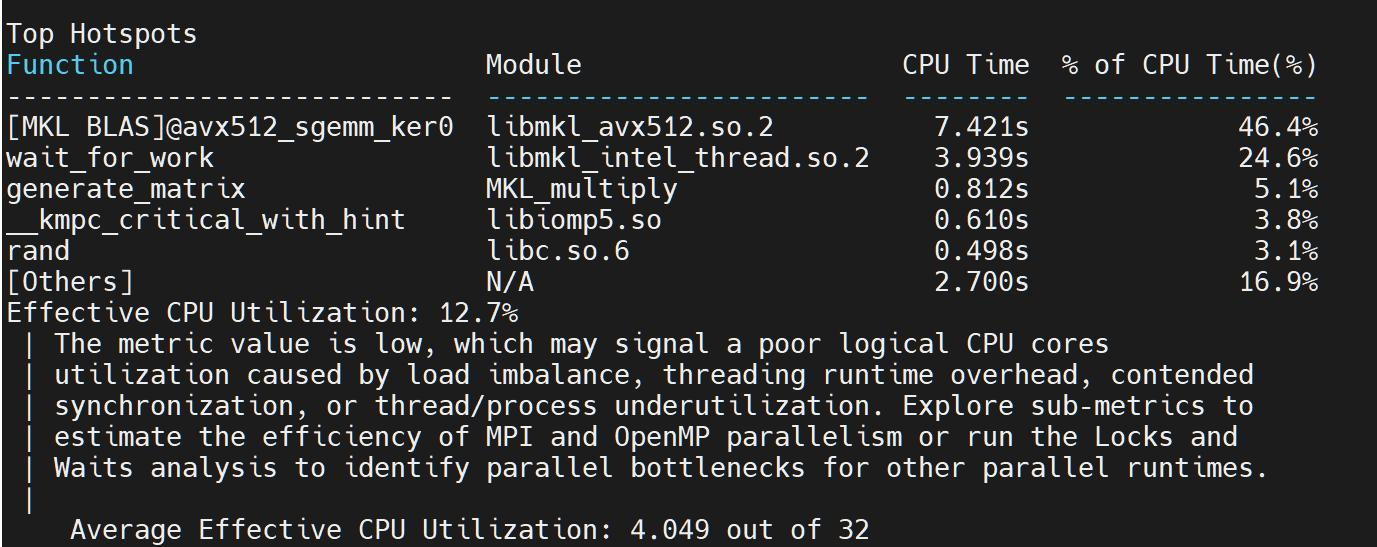
我们来看看Intel MKL的热力图：

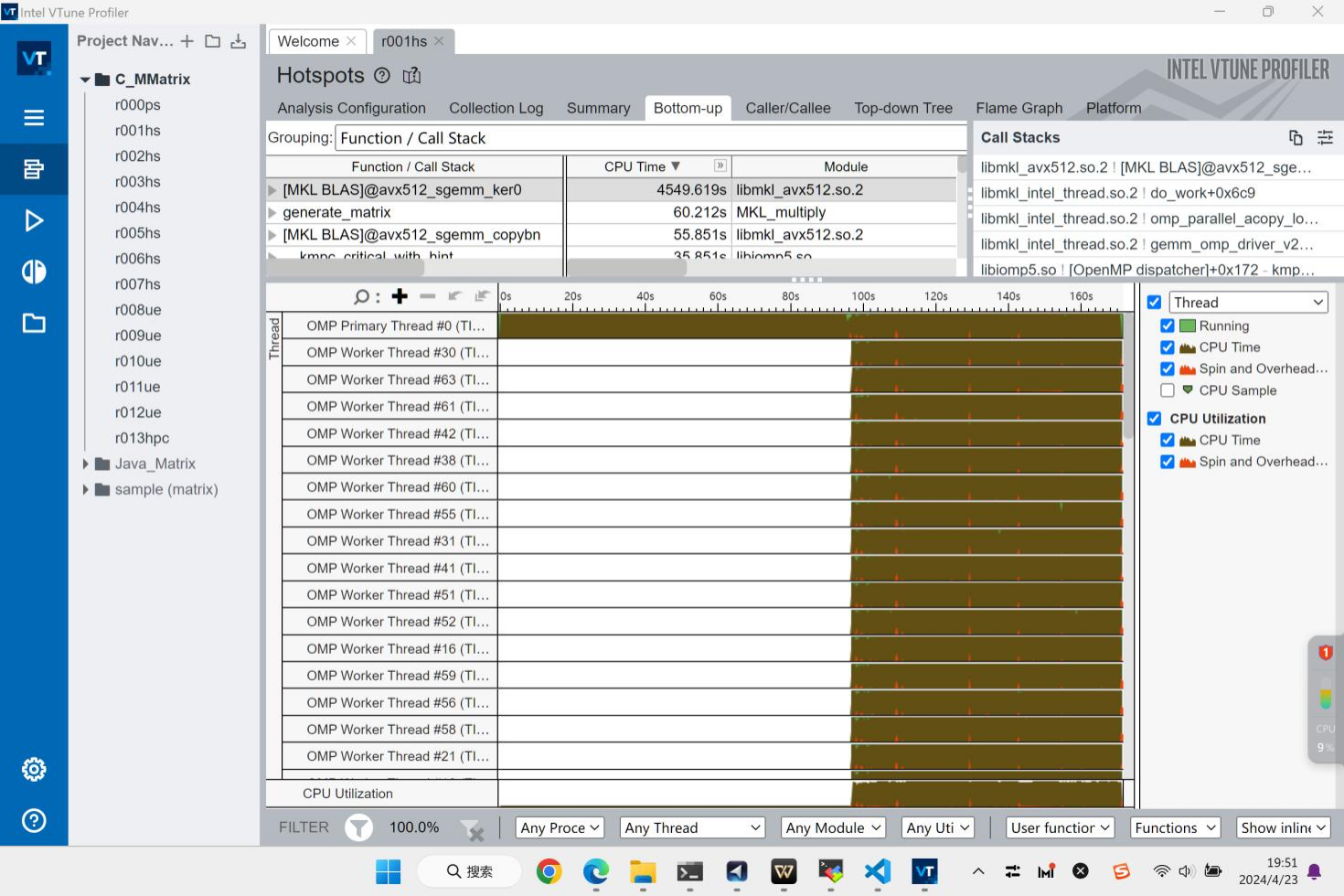
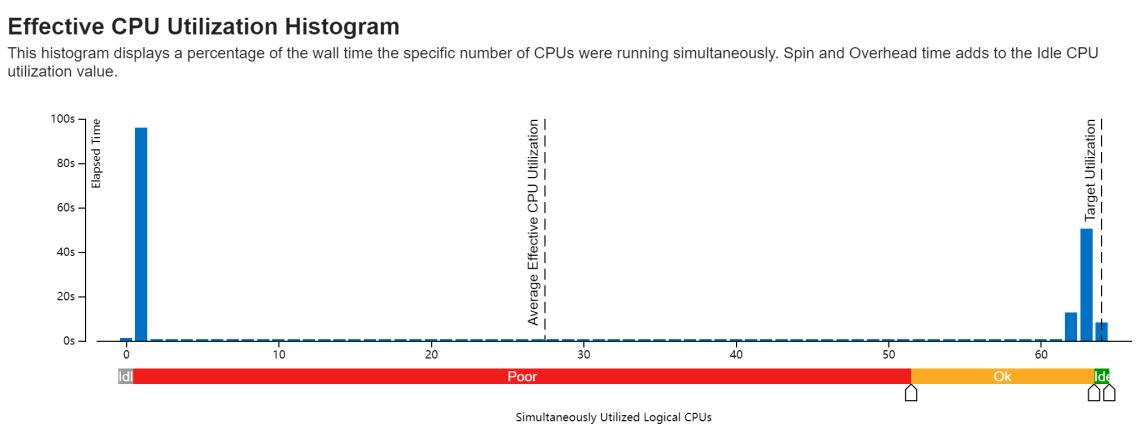
开始的单线程是我写的初始化矩阵，不记入时间。在矩阵初始化完成后，OpenMP就开始创建63个Worker Thread，他们会同步开始工作。有趣的是，这些CPU线程在Spin等待状态的时间几乎一致，且在程序终止前也进行了Spin，推测可能是在进行数据同步。

MKL似乎很精准地知道我使用了64个核，采用了63核的计算设计，并且尽可能地将CPU的使用频率用到了最满。那么MKL用了哪些代码呢？我们看Caller/Callee。

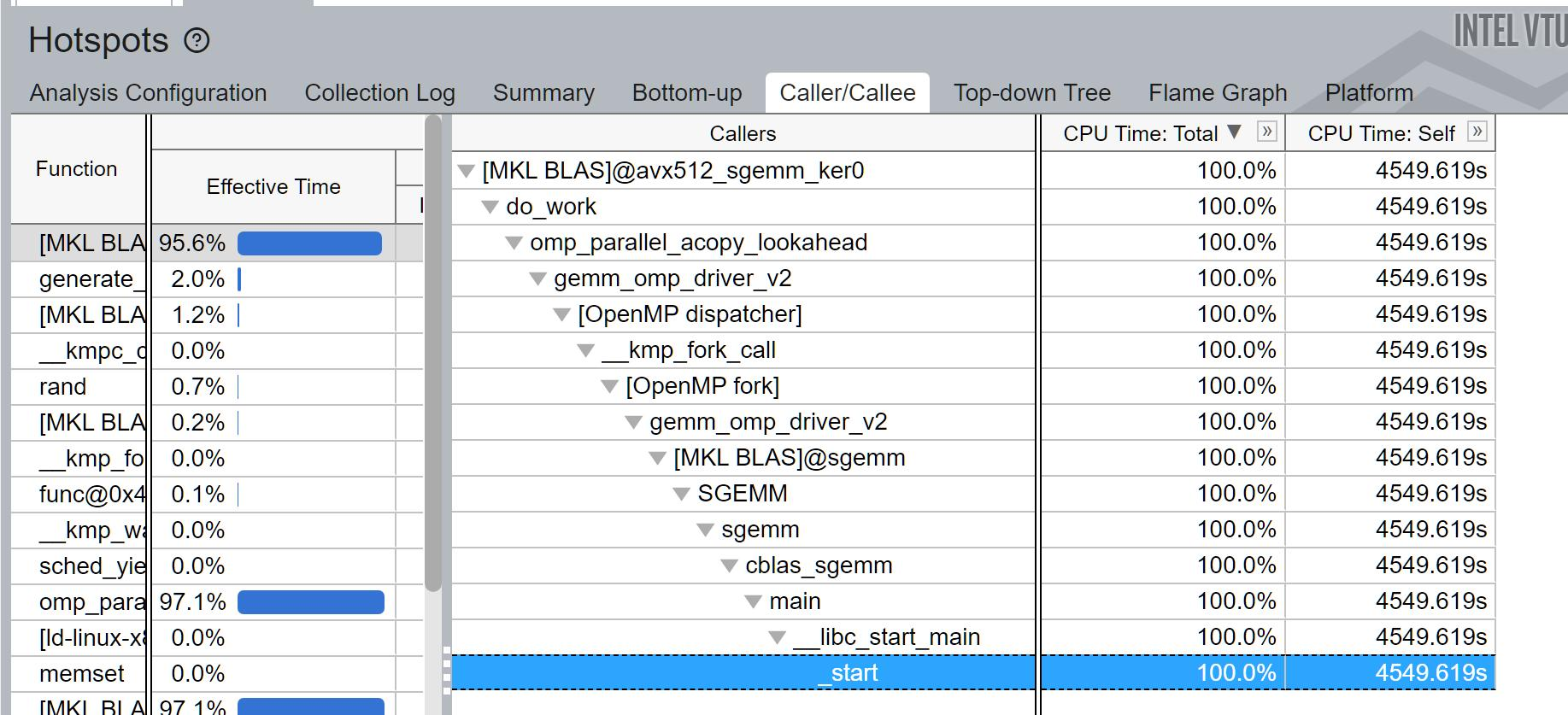
可以看到，程序先是进入了Project2我们探索过的_start和__libc_start_main启动函数，然后进入我们的main函数中。接着，函数进入到MKL的SGEMM函数中。[MKL BLAS]@sgemm是Intel MKL的Interface层，它启动了gemm_omp_driver_v2 driver。诶？这个v2是什么？是不是志强2代处理器的意思？

我猜测MKL把集群的6338当成2代处理了，但是这挺矛盾的，因为6338是第三代志强，Intel怎么连自家的CPU都会不认识呢？当然这一切是我的推测。

回到正题，v2 driver开启OpenMP fork，随后dispatcher 分发命令（也是v2driver），acopy拷贝数据，最后开始调用avx512的sgemm kernel。可以看出，MKL的技术架构跟OpenBLAS一样，是接口-驱动-内核三层操作。

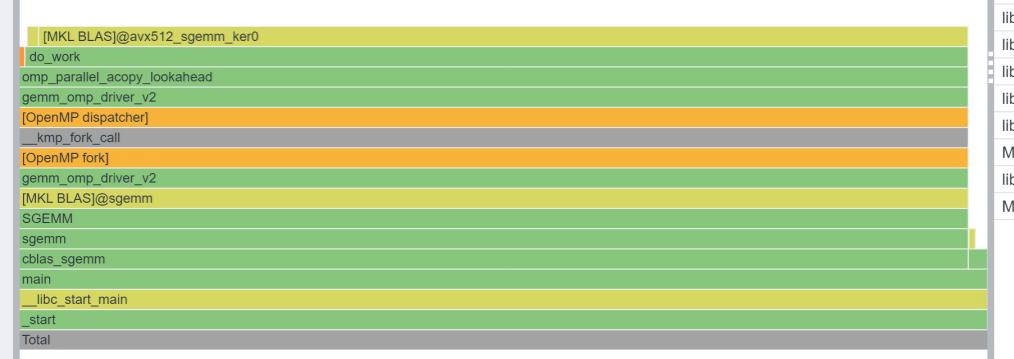
接下来就没有什么好说的，kernel如同一个强大的分布式机器，将所有的任务都分发下去，中间有几次合并，到最后用一点点的时间进行汇总输出。全程手起刀落，驱动不超过100ms,分发占用时间不超过1秒。MKL就像是一个合作紧密的传说级大学Project小组，在组长发布命令后大家各干各的，结果还都干对了。

我们接下来看看OpenBLAS。

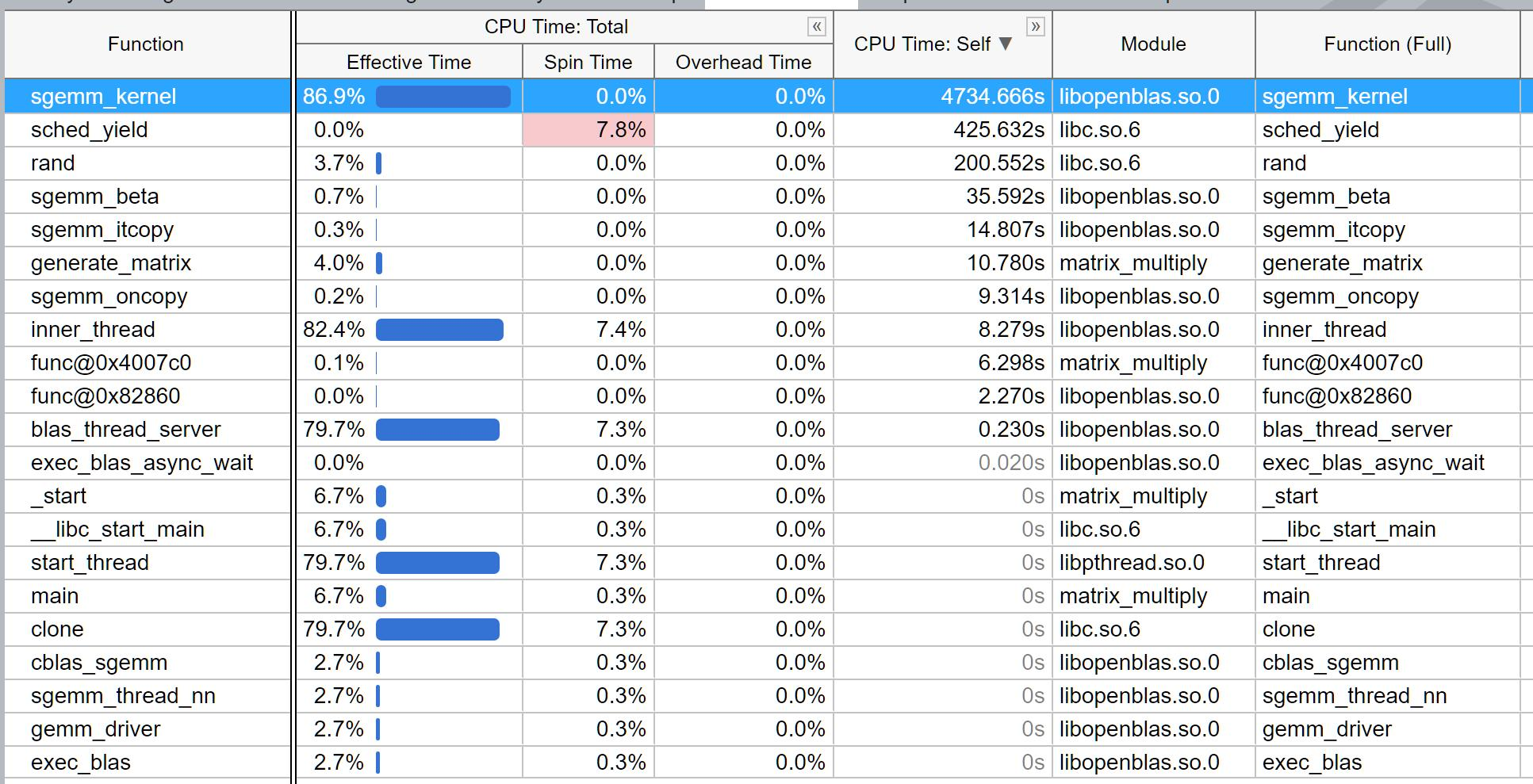
跟Intel不同的是，OpenBLAS并没有显示出它用了哪个具体的驱动，只有一个简单的cblas_sgemm接口与gemm_driver，之后就进入到矩阵的oncopy和kernel。不过，它比MKL多了一个sched_yield，这是什么玩意？为什么它还会Spin？

在网上搜索sched_yield，发现它居然是一个Linux函数，它负责高级进程管理。它实现了内核中最重要的功能，当需要执行实际的调度时，直接调用shedule()，进程就停止了，而另一个新的进程占据了 CPU.。

sched_yield让出CPU后，该线程处于就绪状态，而调用sleep后，线程处于阻塞状态，唤醒后需要先转为就绪状态才能执行。这一块一眼OS，所以直接掏出上学期学的操作系统：

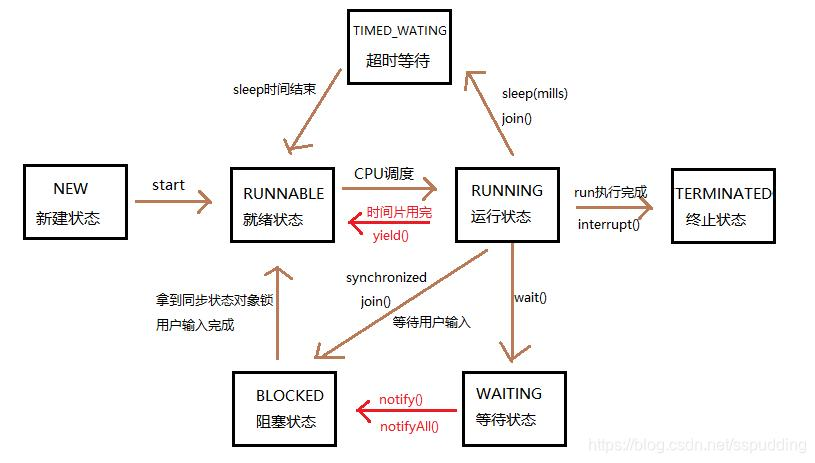
原来如此，原来如此，死去的记忆突然开始攻击我。看来我们的程序在运行途中被终止，然后被另一个线程所占用，这导致了我们的Spin time非常的高。为什么呢？

仔细观察，好像这里边OpenBLAS没有OpenMP的函数？看热力图里也没有调用。并且CPU的Spin频率非常高，看起来不像是在做纯计算，而是在通信什么的。难道此时OpenBLAS是多进程模型？

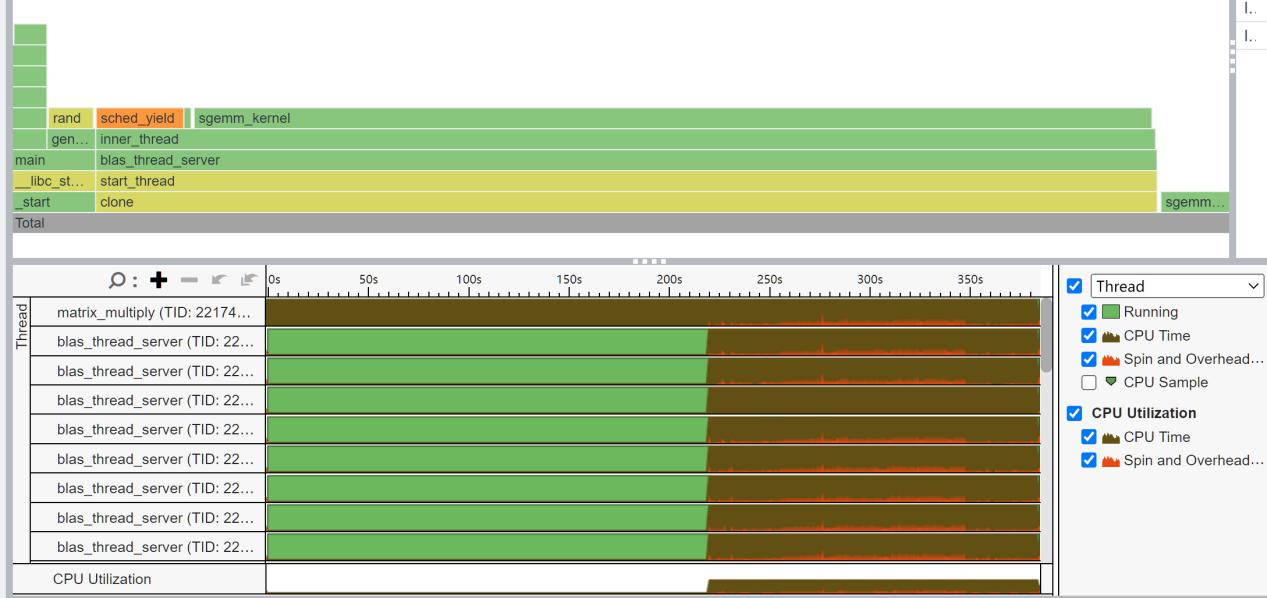
我又查询了一下，似乎是编译时的问题，我在编译时没有使用OpenMP选项：

make USE_OPENMP=1

之后程序运行效果如下：

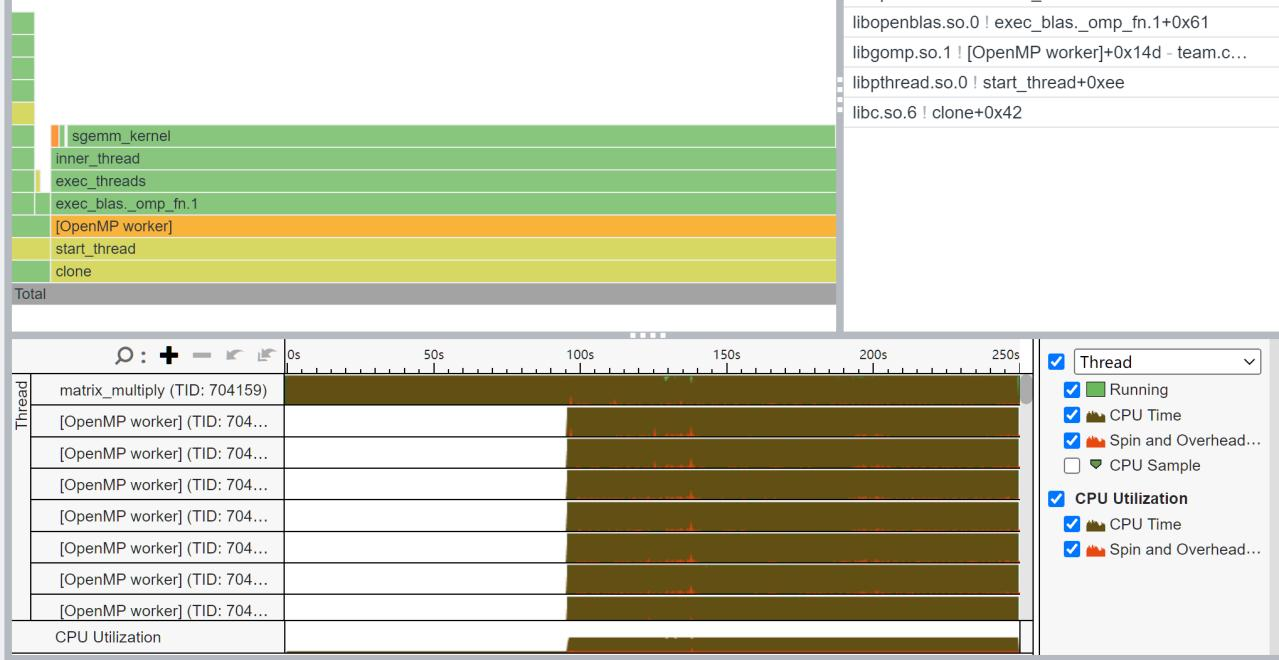
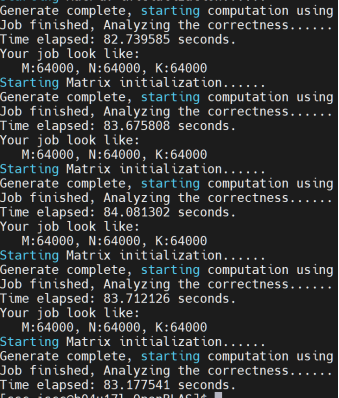
没想到OpenBLAS的OpenMP居然是手动开的。那等等，那OpenBLAS在之前的线程并行上用的是谁？

于是我阅读了文章[29]，这篇文章讲述的是OpenMP是如何实现的。OpenMP使用fork-join并行机制，程序开始串行执行，此时只有一个主线程，然后在遇到用户定义的并行区域时创建出一组线程。在并行区域之内，多个线程可以执行相同的代码块，或使用工作共享结构体并行执行不同的任务。

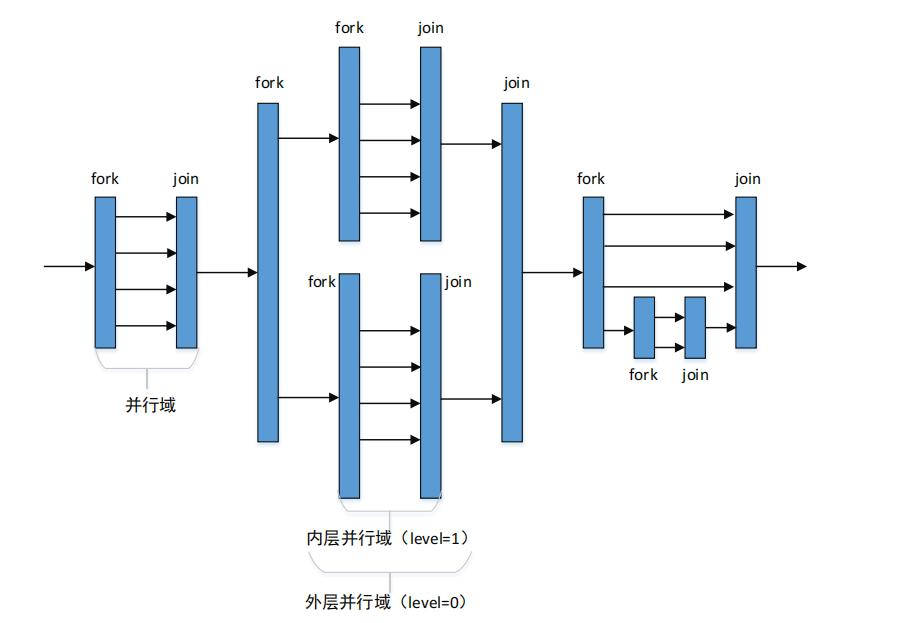
从系统层来说，OpenMP在并行域用的是操作系统的线程，这些线程在物理上会对应到我们服务器的具体的各个CPU上。

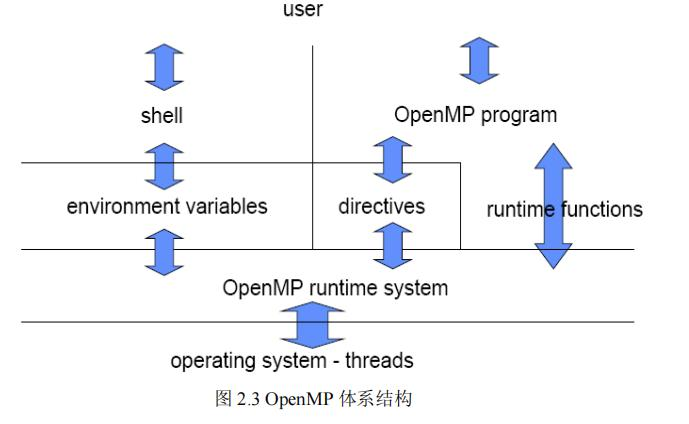
但是，具体OpenMP是怎么分配线程和数据的呢？这里边的关键在于，如何根据硬件，即线程所在的核，和数据所在的内存位置，以最短通信距离、或同时完成计算、或最快调度为具体的目标，来实现具体的分配。

我又读了文章，发现，对于多处理器，我们有 DOALL 循环调度算法，在这类算法中，又细分有因式分解法调度和梯形自调度算法。这类调度算法会考虑数据的位置来提高并行循环的性能。DOALL算法不一定是最好的调度算法，还存在别的几个针对并行的调度算法如DOACROSS 循环调度策略算法。有兴趣的朋友可以看看文章[30]，这里边分析了几种OpenMP调度的机制。

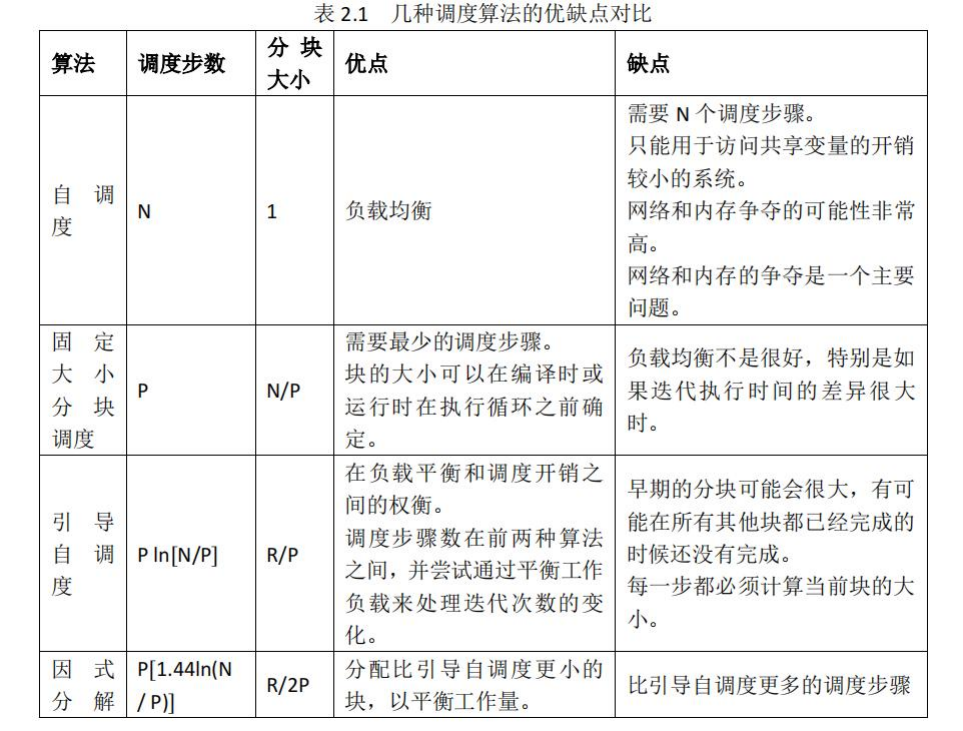
因此我们可以看到，在这些机制当中，我们在设计OpenMP的时是尽可能希望负载均衡的，也就是让所有的任务基本上在同一时间完成。这听起来挺简单，但是我想起来数据库的Project里的负载均衡，我就知道这个策略有多难了，并且一定多多少少会有一些落后的线程。于是我又查到，其实我们写的OpenMP，背后都会进行隐式同步，意思就是说有个omp barrier,必须所有线程都到达barrier，程序才能继续下去。

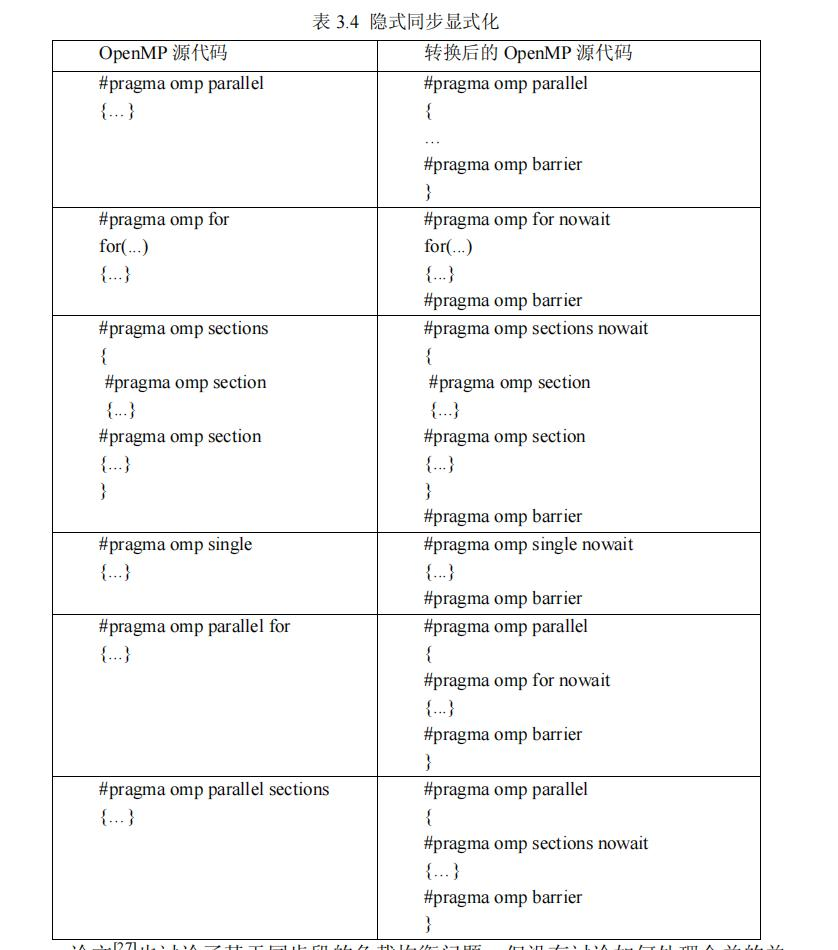
以前我对OpenMP的印象就是咱们加行代码，for循环就可以噼里啪啦地加速了。但是看完这一行背后的算法、优化还有看不懂的硕士论文，我对它肃然起敬。

好我们递归回到上一个问题：如果不用OpenMP，OpenBLAS之前是怎么启动这个32个Worker线程的呢？我这里将两次不同编译过的OpenMP的源码进行了对比，尤其关注在OpenBLAS开启线程时，他们调用的动态库：libpthread.so.0。

看来OpenBLAS用的是POSIX标准里的pthread线程库。POSIX是可移植操作系统接口(Portable Operating System Interface) 的缩写。它是在IEEE 1003.1 标准下定义了应用程序（以及命令行 Shell 和实用程序接口）和 UNIX 操作系统之间的语言接口。就像BLAS库希望能在各种CPU中发挥最大的价值一样，POSIX的目标就是可移植，而这里边就定义了线程的接口。

但是比较神秘的是，OpenBLAS在使用了POSIX后依然使用了OpenMP，可能这里边是用OpenMP做更高级的通信以及api。但是具体我没有研究。但是，我可以说说OpenMP跟POSIX底层里发生了什么。这就要引入我们的Shared Memory Programming Model了。

OpenMP跟POSIX pthread的区别

对于一个单独的进程，我们可以有多个执行的线程，每个线程有自己的数据，在全局也可以有共享的数据。每一个线程可以通过修改全局数据来实现相互通信。

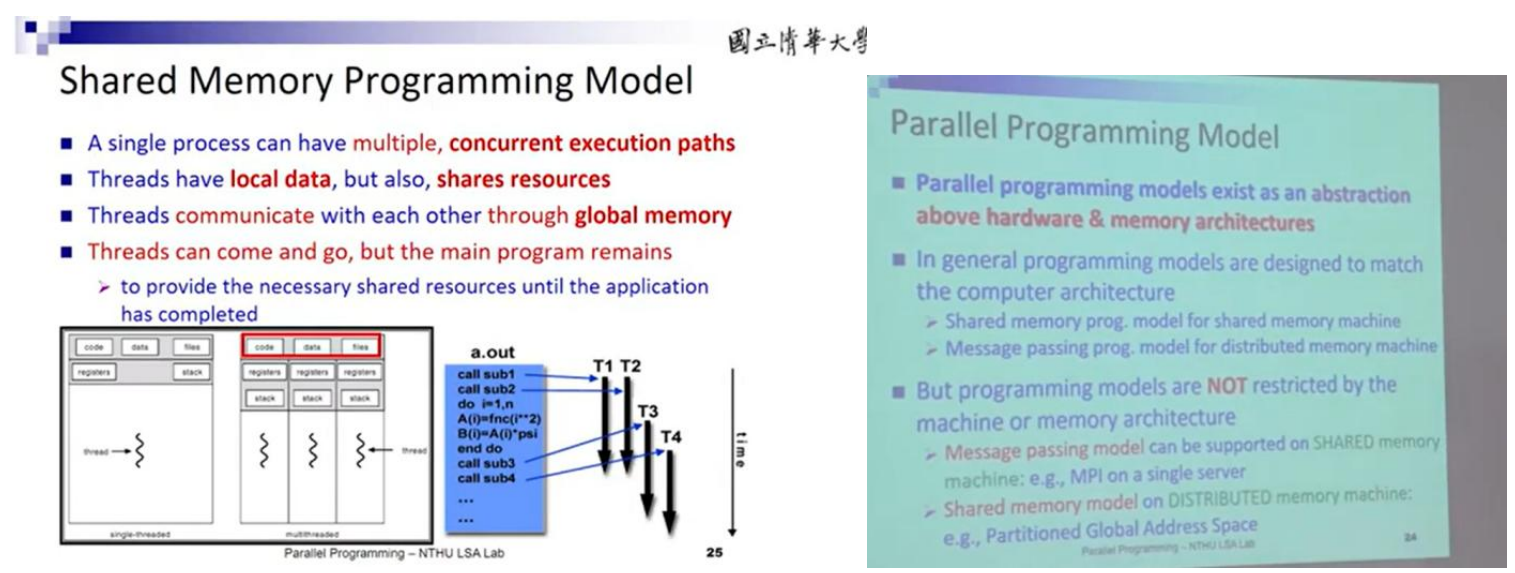
那么在实现层面，有两种实现的方法。方法1是创造出pthread库，然后运用线程库创造线程，销毁线程等等。另一种实现的方法是在编译的时候交给编译器处理，也就是OpenMP。

这是SMPM，共享内存编程模型的实现的想法。另一种并行模型MPI，是消息通信模型。这个模型比起使用一个共同的共享内存等想法，它更多是使用Mem copy来将数据通信到别的线程的内存中。MPI的好处就在于它不再受到L2 L3缓存等物理限制，在网络等连接下，它可以不断地扩展。

这两种模型各有好坏。像OpenMP这样的模型对底层更加接近，对L2 L3 Cache的亲和力更强，在同一台节点内的速度比MPI更强，MPI是直接在相应的线程内复制通信，而OpenMP的灵活度更高。但是OpenMP就无法进行多节点的设计。因此更多时候程序设计应该是考虑OpenMP+MPI的操作，这也是HPL的设计模式。

另外值得一提的是，MKL用的是自研的iomp，它也实现了OpenMP的接口，但是不开放给我们使用。MKL基本上算是闭源生态。

在OpenBLAS的kernel部分是长长的SIMD指令集。vfmadd231ps是一个融合乘加指令，具体如下：

VBROADCAST是从内存中拿出浮点数，然后给各个核计算。

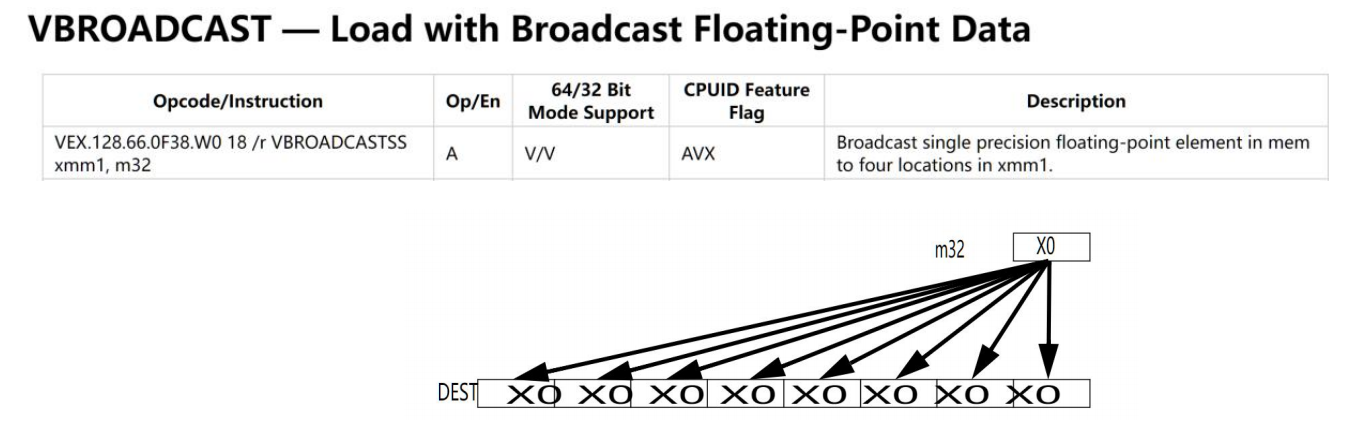
然后就是，更新循环（add），load数据，计算乘加，重复1万次。这里边有个道道，就是我们的乘加指令跟我们的load指令应该如何分配的问题，是每2次加指令然后load还是每3次加指令然后load。我们这里就可以对不同的机器、指令进行优化。

Address Source Line Assembly CPU Time: Total CPU Time: Self
0x2bd7df 0 vfmadd231ps %zmm4, %zmm7, %zmm18 0.1% 2.890s
0x2bd7e5 0 vfmadd231ps %zmm5, %zmm7, %zmm19 0.0% 0.750s
0x2bd7eb 0 add $0x10, %r8 0.0% 0.340s
0x2bd7ef 0 vbroadcastsdq  (%r15), %zmm6 0.0% 0.110s
0x2bd7f5 0 vfmadd231ps %zmm4, %zmm6, %zmm20 0.0% 0.310s
0x2bd7fb 0 vfmadd231ps %zmm5, %zmm6, %zmm21 0.0% 0.480s
0x2bd801 0 vbroadcastsdq  0x8(%r15), %zmm7 0.0% 0.270s
0x2bd808 0 vfmadd231ps %zmm4, %zmm7, %zmm22 0.0% 2.190s
0x2bd80e 0 vfmadd231ps %zmm5, %zmm7, %zmm23 0.0% 0.620s
0x2bd814 0 vbroadcastsdq  (%r15,%r12,1), %zmm6 0.0% 0.300s
0x2bd81b 0 vfmadd231ps %zmm4, %zmm6, %zmm24 0.0% 0.310s
0x2bd821 0 vfmadd231ps %zmm5, %zmm6, %zmm25 0.0% 0.330s
0x2bd827 0 vbroadcastsdq  0x8(%r15,%r12,1), %zmm7 0.0% 0.180s
0x2bd82f 0 vfmadd231ps %zmm4, %zmm7, %zmm26 0.0% 1.330s
0x2bd835 0 vfmadd231ps %zmm5, %zmm7, %zmm27 0.0% 0.440s
0x2bd83b 0 vbroadcastsdq  (%r15,%r12,2), %zmm6 0.0% 0.250s
0x2bd842 0 vfmadd231ps %zmm4, %zmm6, %zmm28 0.0% 0.320s
0x2bd848 0 vfmadd231ps %zmm5, %zmm6, %zmm29 0.0% 0.390s
0x2bd84e 0 vbroadcastsdq  0x8(%r15,%r12,2), %zmm7 0.0% 0.350s
0x2bd856 0 vfmadd231ps %zmm4, %zmm7, %zmm30 0.0% 0.670s
0x2bd85c 0 vfmadd231ps %zmm5, %zmm7, %zmm31 0.0% 0.340s

文章[4]讲述的就是在HPL的BLAS上进行优化处理。HPL上使用的是DGEMM，跟SGEMM比较类似。我们可以在后面介绍一下HPL。在他们的机型上，BLAS底层的SIMD指令中的计算-访存就是3:1。而文章[28]是中科院对国产申威处理器进行的BLAS优化，在这里他们的计算-访存指令比就是1:1。他们提到，申威处理器硬件提供两条流水线, 无数据依赖的计算与访存可同时发射, 则指令排布应尽量保证一条计算指令和一条取数指令共同出现, 使得两条流水线都占满。

而两条流水线在执行命令的时候，会采用比较经典的OoO（乱序执行）的操作，因此这样的指令排布会很好地吃尽CPU（有个教程讲的挺好，虽然是关于CUDA的：https://www.bilibili.com/video/BV1kx411m7Fk/?spm_id_from=333.999.0.0&vd_source=4871cfa497362c1a843af2ecff18ab7f）的资源，有课程[19]中进行了专门介绍（安利一下）。

另外，OpenMP还有一个弱点。我一开始是在启明的登录节点上进行的编译，登录节点上只有32个核，这导致我们的程序最终只使用了一半的核数。这也告诉我们OpenBLAS的一个弱点：必须要在相应的节点上才能产生相应的最好的driver和kernel。但是MKL就不是，MKL作为动态库可以自动选择，不用担心数学库和机型不匹配的问题。

我又重新测了一遍OpenBLAS，这回，数据变的比较接近了。虽然还是没能打过MKL的70秒，但是83秒的平均成绩也是非常优秀的了。在我意识到编译这个问题之前，我是以为OpenBLAS在判断失误。它可能认为NUMA节点的通信损失大于了计算带来的优势。

“访存-计算”平衡是我们接下来需要考虑的一个很重要的点。另外就是，MKL确实作为一个闭源的数学库，在加速方面还是挺有实力的。

MKL的技术

我们来看看MKL还有什么黑科技：

首先第一个，对于稀疏矩阵，MKL提供了对稀疏矩阵的优化API，OpenBLAS似乎没有看到（可能单纯是我没有找到发现）。在稀疏矩阵直接法求解中一个常见的技术是矩阵重排，通过矩阵重排，可以使得矩阵的带宽减小（非0元素位置相对更趋近于对角线），从而使得直接求解效率更高，一种常见的矩阵重排方法是Cuthill_McKee算法。不过MKL在这里用的是基于 FEAST 的子空间投影算法和经典的 Krylov 子空间迭代方法。

第二个黑科技是ASC里中山大学的队长告诉我们的：MKL会使用JIT技术对小规模矩阵的乘法进行加速[15]。这个JIT并非像我们Project2里Java的JIT，把字节码翻译成机器码，它是直接改动底层的自己的机器码。面对小矩阵，我们从刚刚的测试中可以看到MKL的表现其实并没有特别的好。我个人推测MKL可能它自己在内部有很多的选择分支以及线程分配，导致在小矩阵上通信的成本增加了。而JIT技术就会将Kernel的大小、循环调整以及我们的计算-访存指令比例为最适合的我们机器的形状，随后进行加速计算。

具体的实验我进行了比对：拿MKL计算1000次矩阵乘法，比较时间。拿自己实现的乘法计算1000次，比较时间。主要目的是看我们的cache hit会不会影响到我们的加速。如果在同样的缓存下，MKL的结果还得到了加速的话，我们可以认为MKL就进行了加速。

综上，我测试了OpenBLAS跟MKL的平均运行时间。随后分析了他们的内部特性。我认为我们对抗他们的优缺点如下：

	我们的BLAS	OpenBLAS	MKL
核数	对自身硬件有确定性了解	并非完全了解。需要特定编译选项	对硬件了解合理，可以动态调整。但是会花费一些时间
通信	采用OpenMP，更轻量	采用POSIX线程库	采用自研iomp，多核多节点强
计算访存指令占比	自行设计	2计算/访存	动态JIT Kernel
非计算分支	少	中等，如选择driver	多，如JIT
SIMD	AVX2/AVX512	AVX512	AVX512
alpha，beta	不需要	需要计算	需要计算

Part 5: 优化方案                         Chapter 5: KILL BILL

面对5个规模的矩阵，我们针对每种矩阵规模，分别对OpenBLAS和Intel MKL发起挑战。我们要关注自己的访存-计算平衡，尽可能让核数跟访存对应上。下面介绍中的具体图片来自于CPP github appendix ppt。

5.1 击败16 x 16                            Vernita Green*     

这个矩阵非常小，因此计算的时候其实更像拼刺刀，我们利用对手的分支过多，直接相乘就可以战胜了。当然为了更快，我们使用SIMD指令。这里我也进行了测试，用AVX2好还是用AVX512好。我的结果是AVX2性能更佳。

不同机型上的AVX512指令实现方式是不一样的。AVX512指令集是Intel提出的，Intel专门做了一个处理单元。在AVX2的基础上数据寄存器宽度、数量以及FMA单元（乘积累加指令单元）的宽度都增加了一倍，所以在每个时钟周期内可以打包8次双精度和16次单精度浮点运算。但是AMD上的AVX512指令其实是靠两个AVX2单元组合拼接实现的。这部分的性能有机会可以做一个对比。

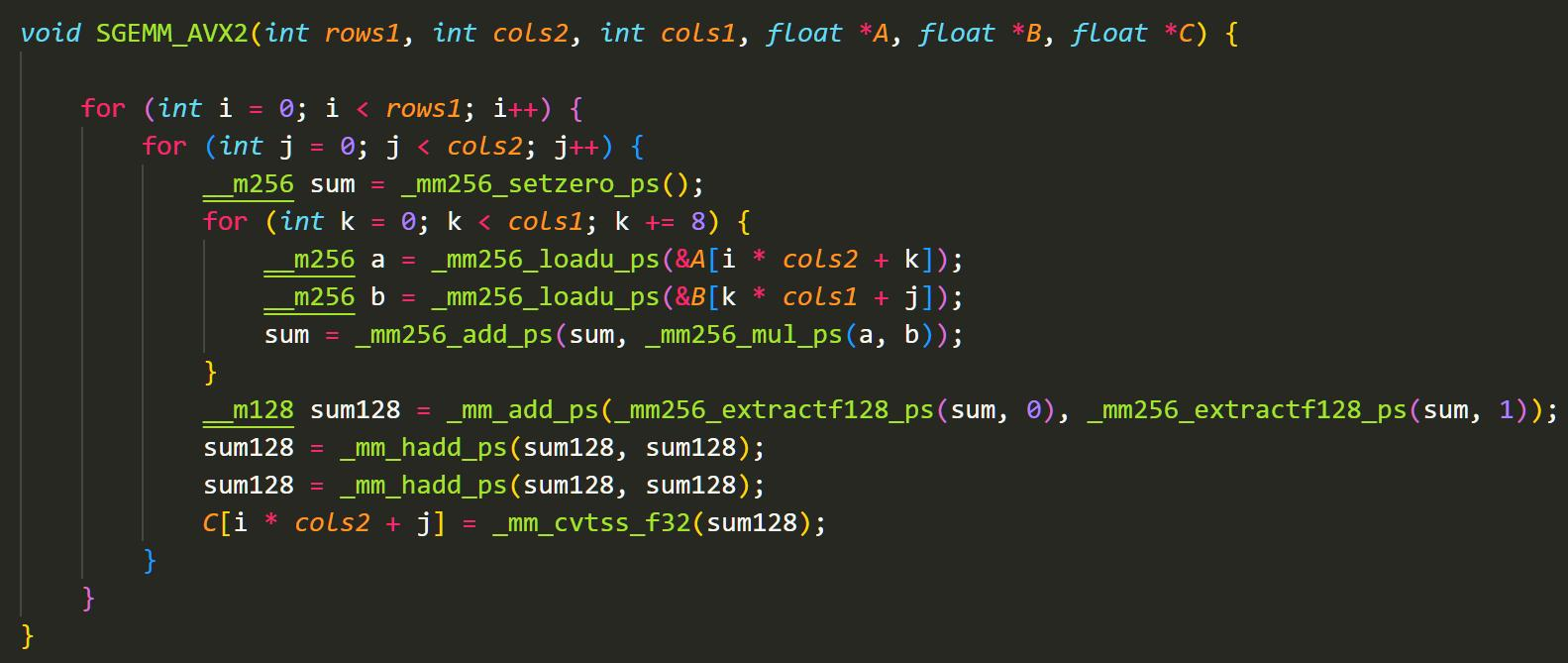
5.2 击败128 x 128                O-ren Ishi

128大小的矩阵经过测试，使用AVX512指令会更好。同时，将j和i的顺序调换，增加了B矩阵的Cache hit的概率（j变量的变化更少，使得更多数据得以重复利用）。不要使用OpenMP，我们的L1 Cache大小是1.5MB，足够我们装下所有的数字（64kb）。

5.3 击败 1K x 1K                        Budd

1K*1K的矩阵大约占用3.81MB，访存-计算的平衡发生了移动。分配到每个核的话大概是3-4个核。我们使用 OpenMP+循环展开 击败：

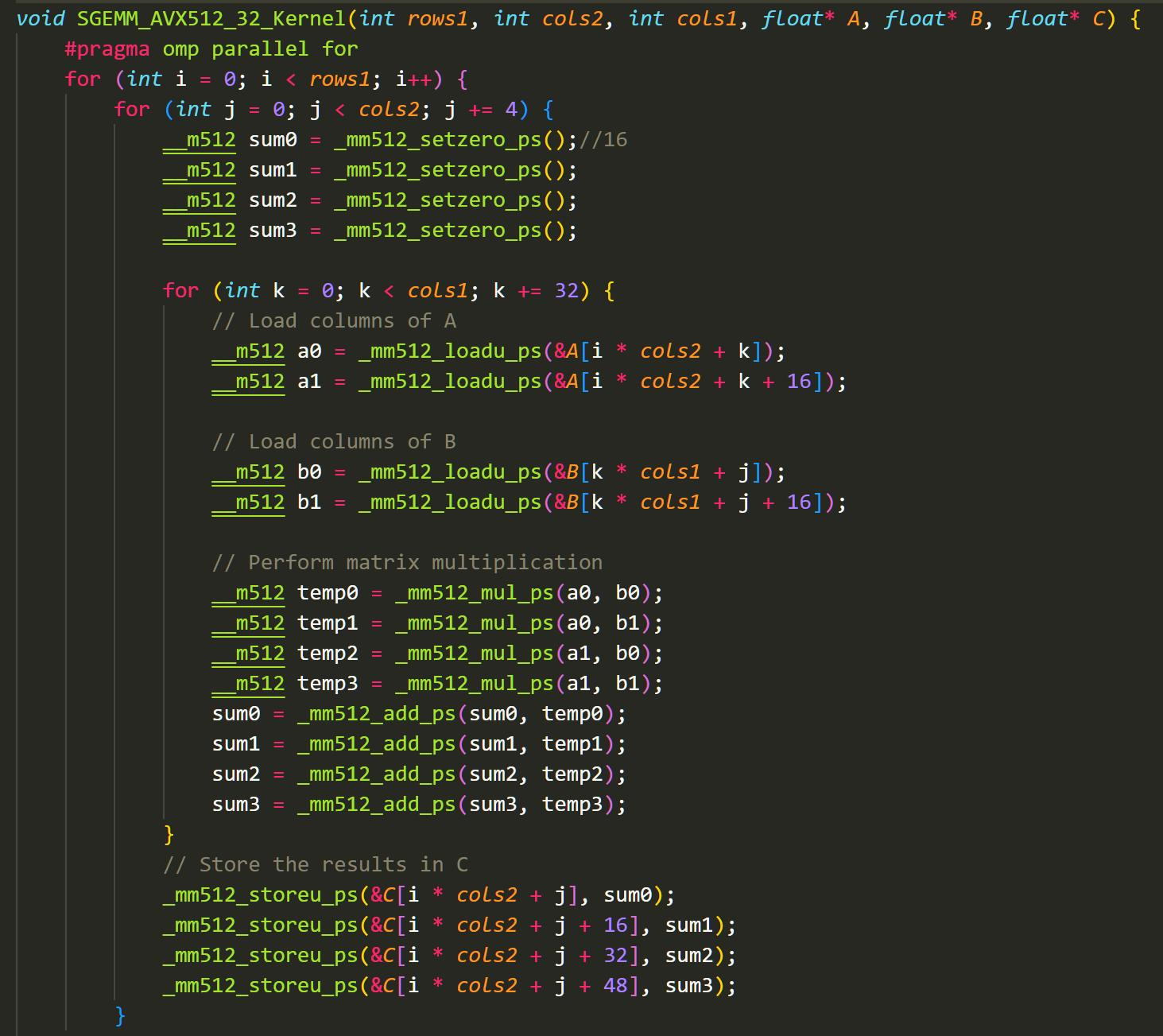
循环展开使得循环的相关性消除，让编译器在执行命令时让内部循环可以在不同的核内并行运行。同时可以减少分支预测的可能性。虽然OpenMP也可以设置自动循环展开，但是这里我们熟悉机器与矩阵的大小，因此直接手动进行了设置。

5.4 击败8K x 8K                     Elle

由于我们的数据量增大，访存-计算的平衡继续发生移动。我们需要更多的核。因此，我们尝试用更大的循环展开核 256* 256。

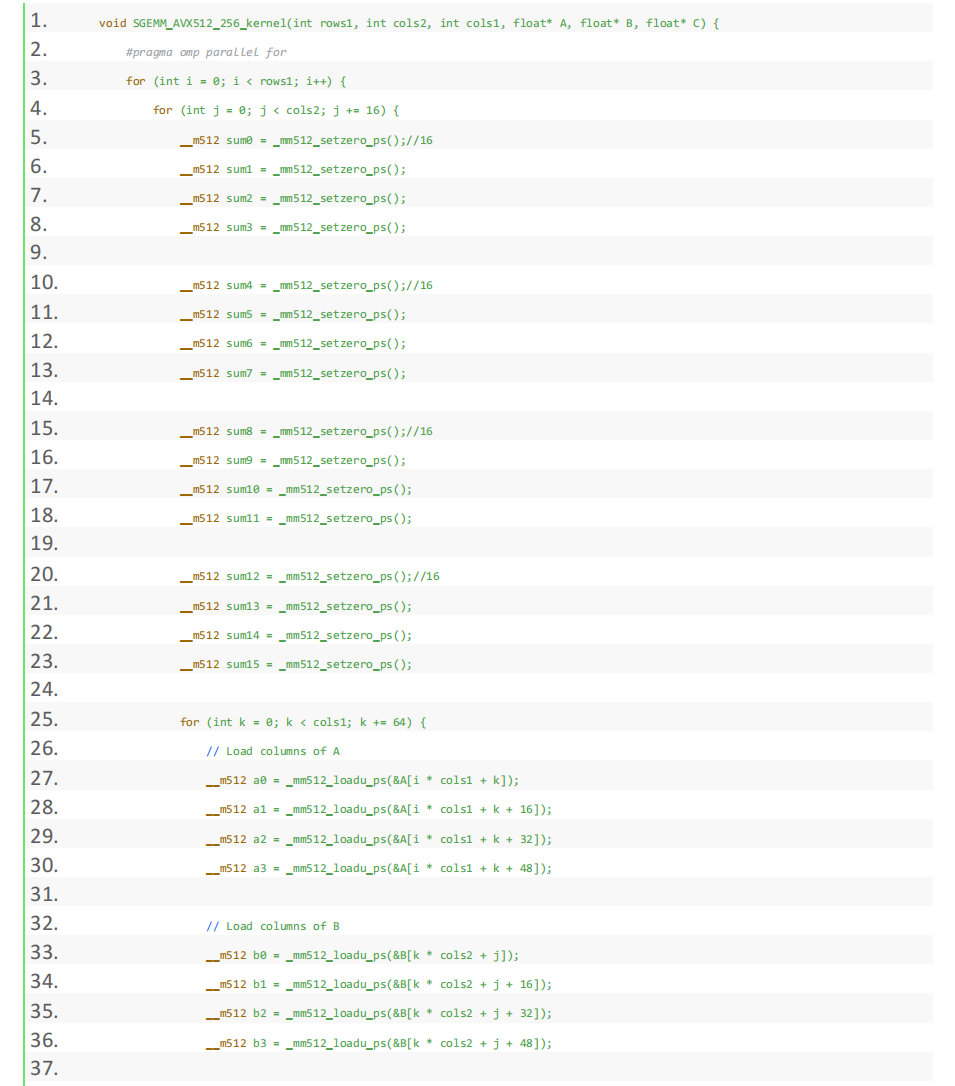
5.5 击败 64K x 64K                             Bill

对于这种大BOSS，我们肯定是要把计算-访存发挥到极致的。而其中我们要尽可能地将访存的成本尽可能减少。因此，我们可以采用分块的想法，给各个核进行分配，然后计算。

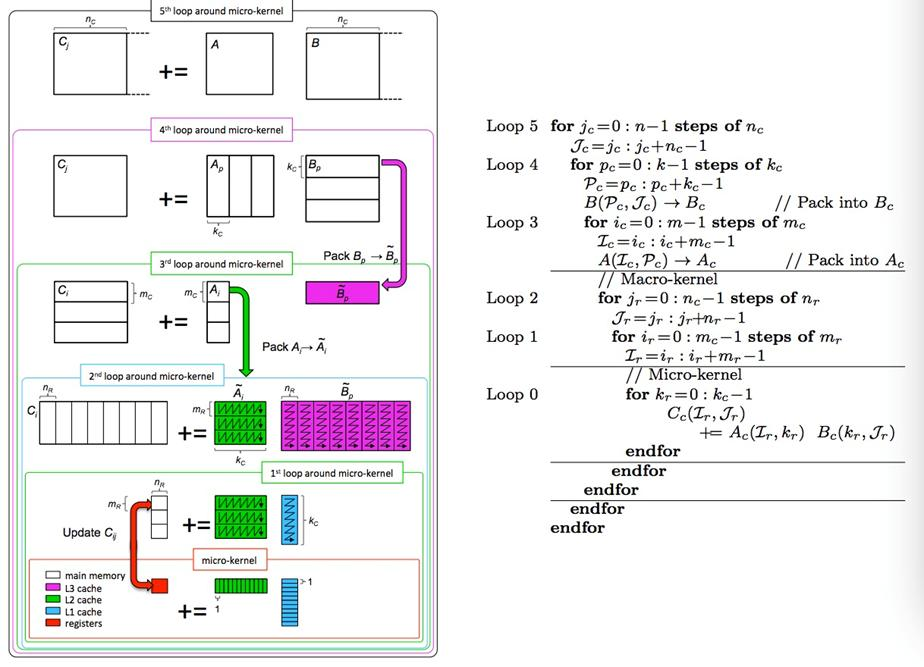
这里有一个问题就是，我们应该用多大的Macro Kernel跟Micro Kernel？我们当然可以自己拿参数进行测试跟调优。一种基于演化计算的自动调优方法由文章[4]给出。他们将Kernel的参数初始化种群，然后进行调优，最后得出他们集群的最佳参数：[792,822,8628]。

使用演化计算当然很不错，可以基本上很准确地找到我们想要的值。但是，如果我们的矩阵太大，计算量太多，那我们可能需要找到一种更高效的方法来寻找参数。对此，我们可以参照下面这篇文章，使用Bayesian Optimization来对程序进行优化。

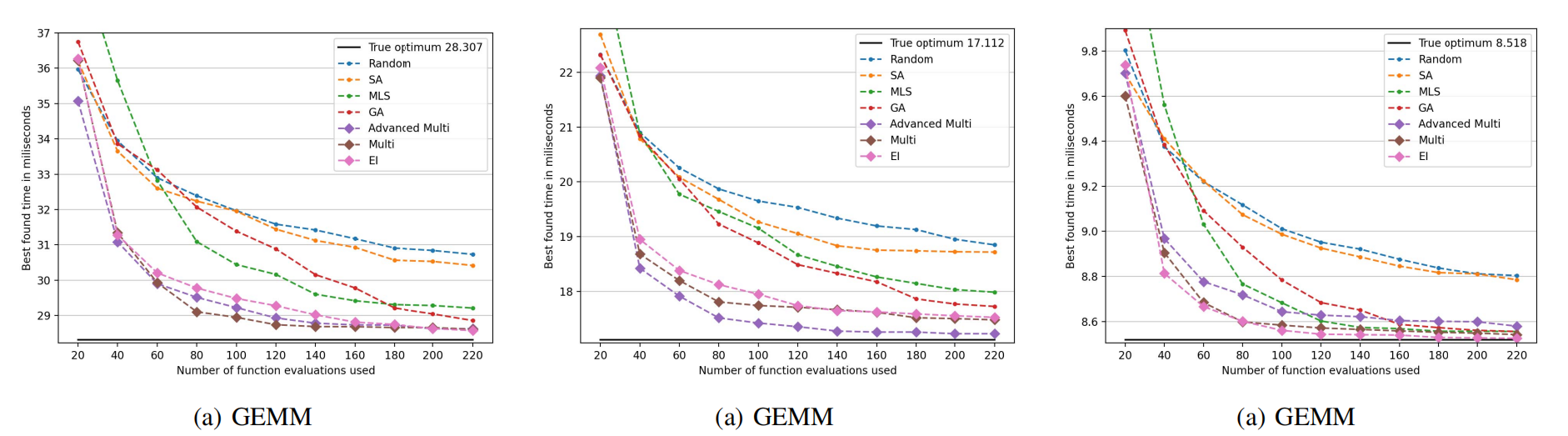
当然，如果我们有CUDA，当然是用GPU更好。对于CUDA，我们可以编辑一个CUDA的核函数，然后进行乘法。GPU使用的是SIMT，单指令多线程。面对一条指令，GPU将启动多个我们之前提到的帕鲁SM，开启多个线程进行计算。跟SIMD相比，SIMT能够在线程数量很多的时候表现的更好一些。回想一下我们刚刚做那些循环展开和指令重排的工作，其实本质上就是希望同时有更多的CPU能执行我们的指令。而SIMT就只需要考虑接收指令，开启线程即可，中间很多的指令不仅可以优化，还可以加速到最优点。

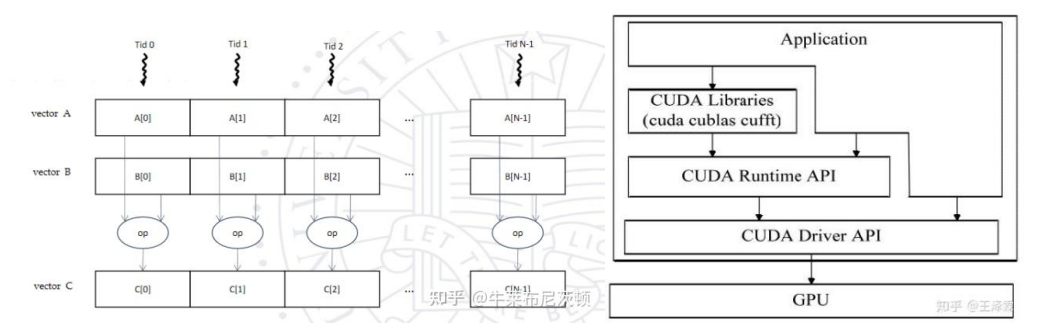
下面的代码仅作为示范：

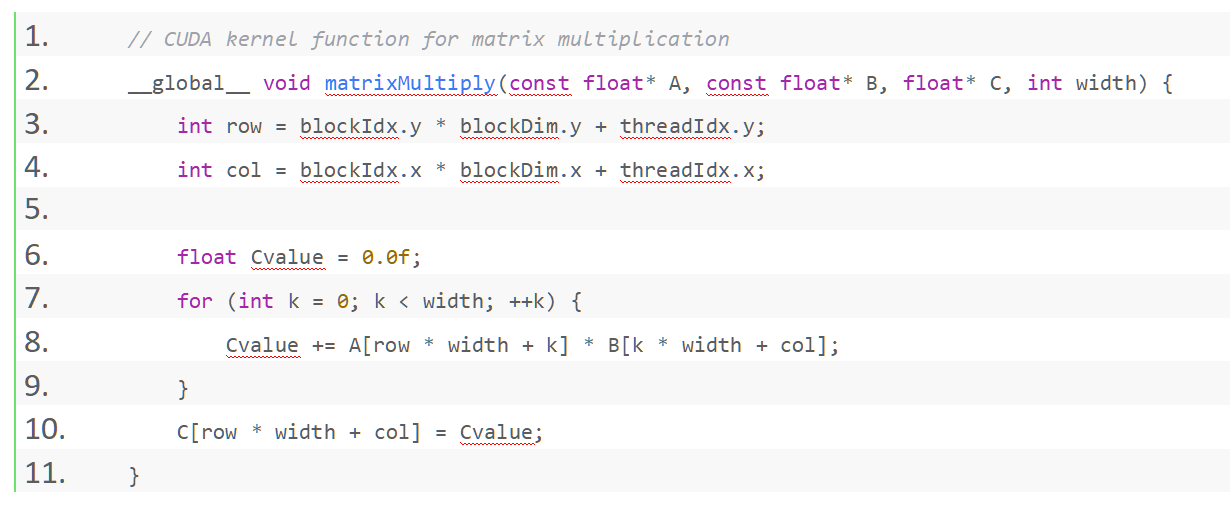
另外值得注意的是，这里如果就这么简单的像我这样写，是无法发挥GPU的性能的，我们还需要进行不断的拓展，在《CUDA C Programming Guide》里就有很好的案例（想快速学习，我们可以查看这篇文章：https://zhuanlan.zhihu.com/p/410278370）。其实优化的目标和方向基本是一致：利用 Shared Memory 降低访存延迟、循环展开、向量读取指令等等。说到头来，还是“计算-访存”优化。另外，还有一个要注意的点是我们的GPU Kernel函数要跟我们的GPU相对应。比如A100的108个SM跟我们2080TI的68个SM就必须在线程模型上进行区分。同时SM内部FP16、FP32、FP8模块的数量都有所不同，如果想极致优化必须考虑到这一点。

更多在异构系统上的优化由文章[3][5][8]给出，他们在我们简单的单节点单GPU的基础上，对多GPU多节点进行了更深入的优化。比如文章[3]完成了一个轻量级跨平台异构加速框架 HPCX，超越了NVIDIA官方的HPL基准测试（但是71.1%的浮点效率其实有点低了，去年我们队在启明上的测试结果在73%左右，可能是文章时间比较久了，现在NVIDIA 24.03版本的HPL可能更强大了）他们的其中一个优化方法计算将访存均匀分布，确保GPU的取存“隐藏”在计算中。

Part 6: 性能测试            Chapter 6: Django Unchained

我们在CS205 Server跟启明上测试。CS205 Server结果如下。我们的速度基本上都在跟OpenBLAS竞争。64K * 64K的矩阵测试不好做，因此没有进行。

在集群上的测试会受到这么两个干扰：虚拟机和他人的程序。虚拟机的策略在于，尽可能地将程序分配在靠近的节点上。但是就算是这样，虚拟机还是带来了一部分的性能损耗。

我们可以用 numactl -c命令查看NUMA节点的结构：

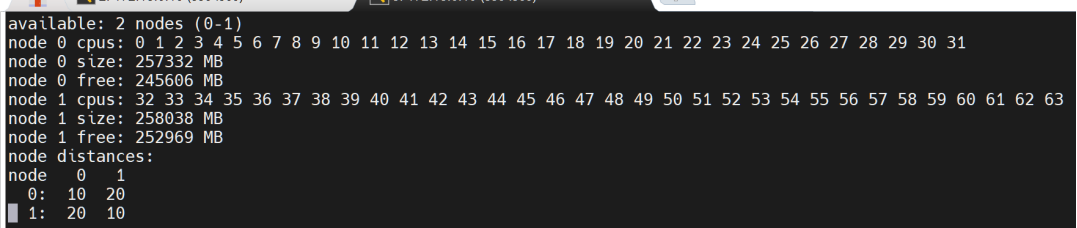
其实通过这个NUMA，我们是不是可以在分块的时候也可以先分成A、B两块，然后再接着计算呢？我觉得这是个不错的想法。不过，这样仅仅适用于占满节点的情况，它还是缺少普适性。

我们也在38队列上进行了测试。测试结果如下：

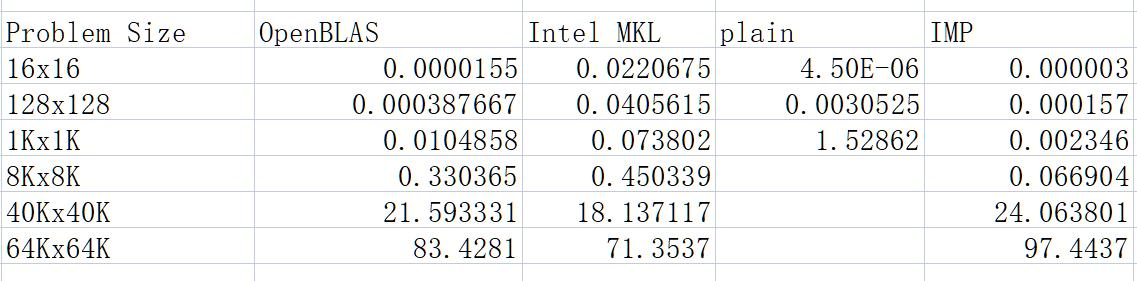
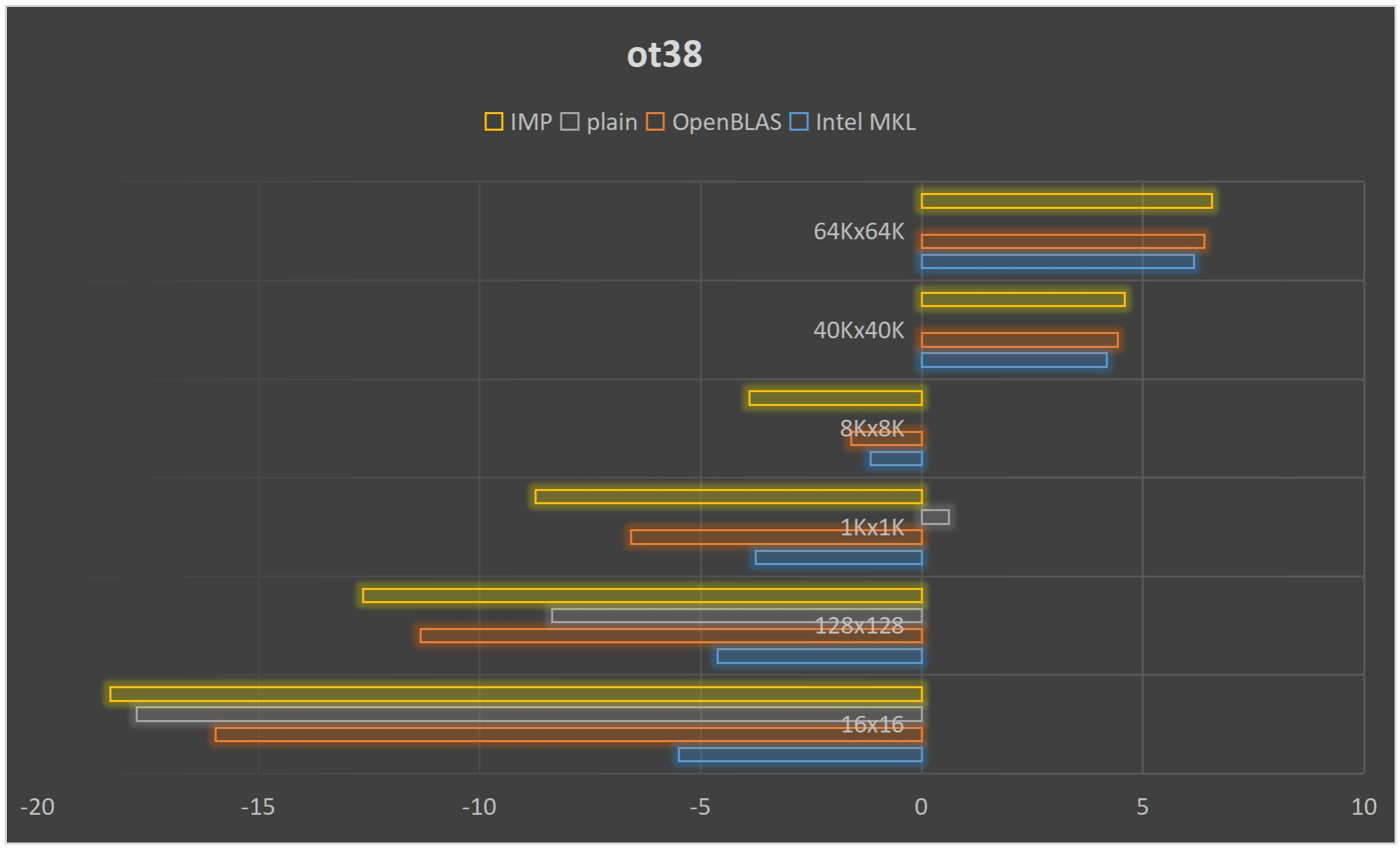
可以看出，在问题规模小于8000时，我们的速度基本上是领先于MKL和OpenBLAS的（没有进行JIT测试），不过在规模达到40K之后，我们的矩阵运行速度就开始减慢，OpenBLAS超越了我们（可能是由于）我们的运行速度基本上在他们下面。不过令人鼓舞的是，OpenBLAS的83秒/21.59秒约等于3.863，MKL的71秒/18秒约等于3.934，我们的大概是在4.05左右，这样的增长速度还能接受。

我们的程序在并行化上还算不错，除了开始的随机化矩阵以外，剩下的基本都是在62-64核。

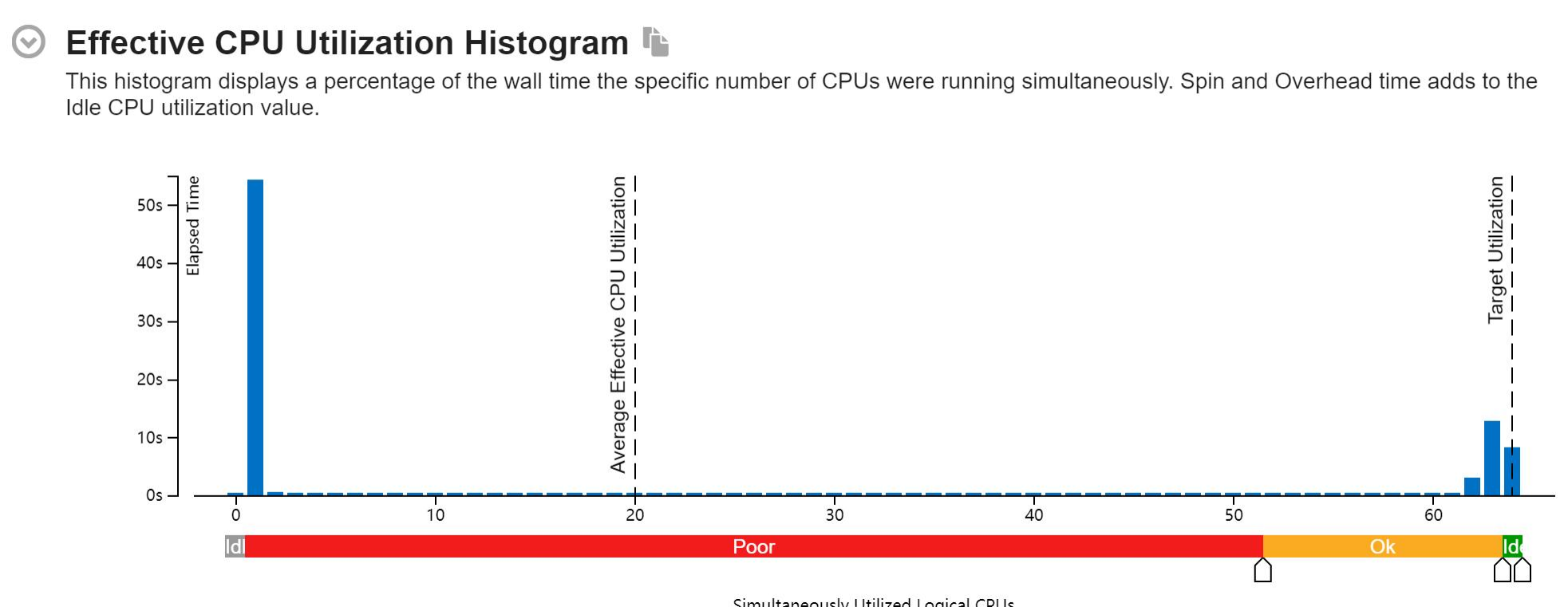
我们的程序在变成汇编指令之后，可以看到程序计算-访存的比例。我认为我们在这方面可以有更强大的进步。另外还有一个点是，我在想可能对于64核的节点，我们的核函数还是有点小了。我们应该做更多的循环展开，就像我们之前看到OpenBLAS的几千行AVX512命令一样。

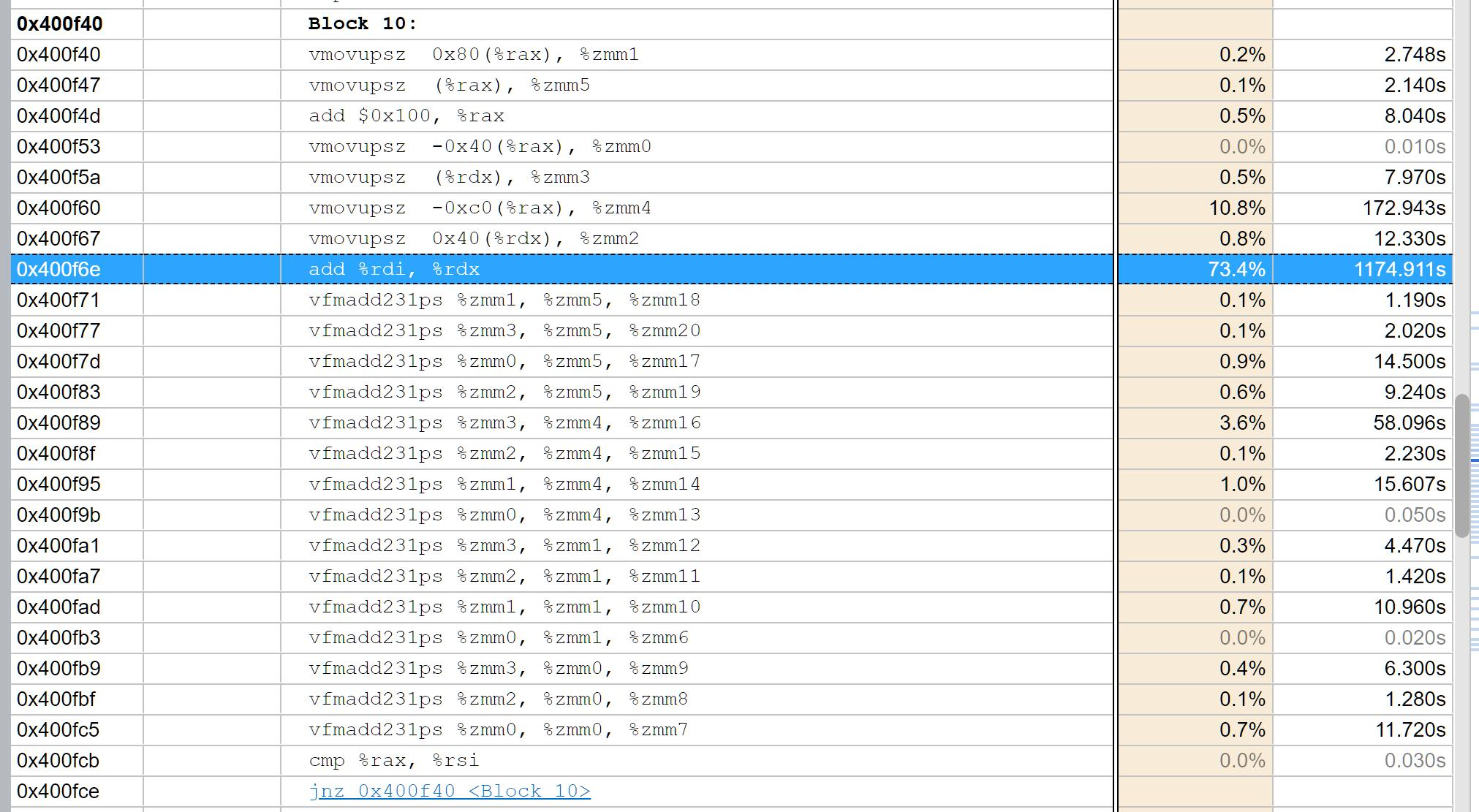
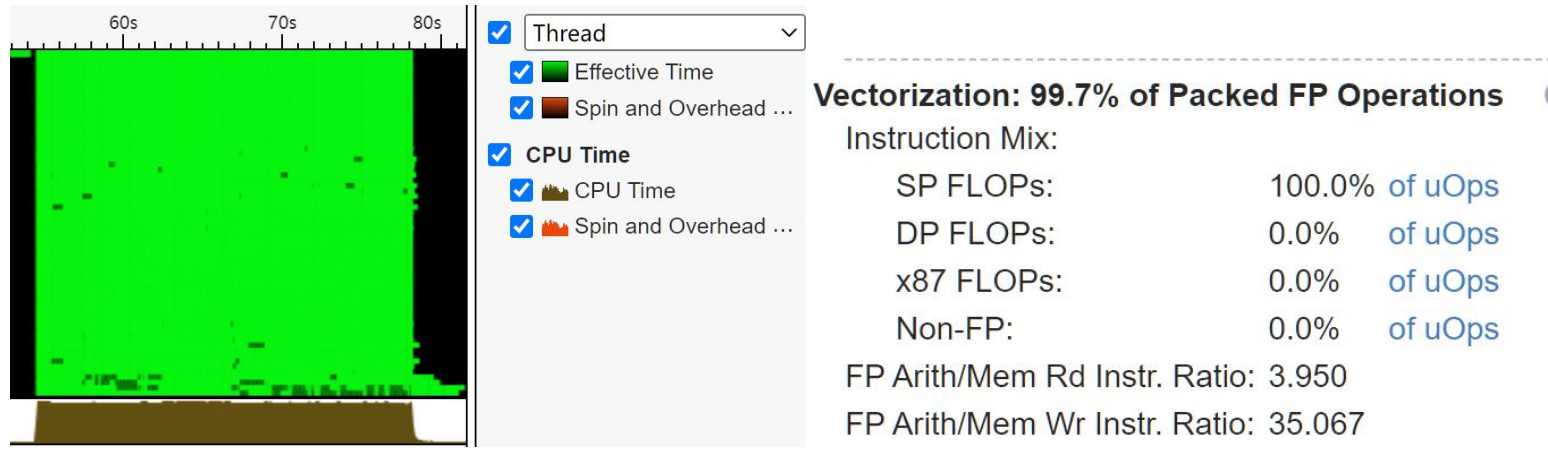
看着还不错的是，我们的CPU基本上的吃满了，只有在少数的情况下中间才出现Spin time。我们程序的CPI非常高，达到了1.96，这应该是SIMD指令导致的。在超线程技术的影响下，普通的load指令CPI大概在0.5左右（Project2），在AVX512指令之后，我们的16条float一次导入，理论性能的加速可能在4倍左右。另外可以看到的是，我们的“计算-访存”的比例在3.95，也就是4左右，这里边如果对比OpenBLAS的2:1，我觉得还是有优化的方向，减少计算的指令，多访存，把存储的效率提高。

有一个很糟糕的事情是，我们在给程序在48核的机器上，用24核来运行时，我们跑的时候跨了NUMA节点，每个节点各12个核，我觉得对此非常的惋惜，如果我就用了一个SOCKET的24核，可能说不定就跟OpenBLAS一样快了。我推测产生这样的原因主要是38队列的服务器有64核，我只申请了24核，而lsf作业系统就给我跨了NUMA节点。可恶，一定是IBM没有看过那篇北大的《虚拟化数据中心资源调度研究》文章！

我们还可以做更多的优化。比如对于Linux操作系统，我们可能可以换成Rocky Linux。他们对线程以及性能的管控比Ubuntu更加高效。我们可以尝试关闭虚拟化等等。当然大部分软件系统架构的改变可遇不可求，在这里也就是简单提提。

我们还可以做更多的分析，比如我们的核时/理论核时，我们的指令数/理想指令数，我们的花费的CPU时间/理论CPU时间等等，来比较我们的访存速度，计算速度，计算开销，得到一个更加全面完善的评估结果。

近年来这些测试还是挺多的。大家对于数据中心好像有了在高性能、高扩展之外，还多了一个节能的需求。听说现在美国数据中心合计功率16.82GW，用电量约192TWh，占其全社会用电量近5%，到2023年，计算中心的电力需求将拉动美国全社会用电量增长10.9%-11.9%（以2023年基准）。所以大家发现，我们不仅要算的快，还要算的便宜，算的高效。（相关文章介绍：https://xueqiu.com/4545671674/287082337 市场规模分析：https://www.mordorintelligence.com/zh-CN/industry-reports/north-america-data-center-power-market-industry）

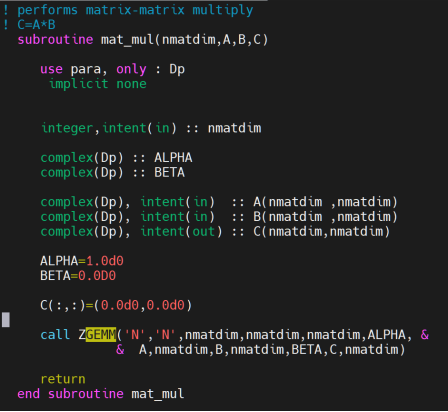
本来我还想把我的程序改成ZGEMM的，计算虚数，然后来加速材料计算的软件。这个软件用于计算石墨烯等材料的朗道能级，它是用Fortran写的，我前两周自己把Fortran学完了，结果没时间改了。我准备后面继续改好我的API，这样就能套上去了。

在ASC比赛的时候，北京大学的队伍就是优化了下面这个api：call ZGEMM，然后把这个api套到了他们自己的GPU BLAS上。我是当时负责这道赛题的同学。我今天回来看，我觉得非常惭愧。我没有在第一时间内对软件进行性能分析，找到软件这里的关键耗时点。同时，北大他们写了一个自研API，就不同的矩阵大小，把计算分配到OpenBLAS、MKL、cuBLAS上。我觉得我们也要有一个，不然我们永远被人家压着打。

不过，这些故事，就可能要慢慢讲了......

Part 7: BLAS、HPL、高性能计算               Chapter 7: SIN CITY

图中中间偏右的这位老先生就是大名鼎鼎的Jack Dongarra, 高性能计算HPC领域的开创者。他参与的一系列线性代数库软件项目，MPI，BLAS，LINPACK，LAPACK，成为了今天高性能数值计算的基石。而数值计算中非常重要的一环，就是GEMM。

Jack Dongarra在他的博士阶段写出了HPL。HPL（The High-Performance Linpack Benchmark）是测试高性能计算集群系统浮点性能的基准程序。HPL通过对高性能计算集群采用高斯消元法求解一元N次稠密线性代数方程组的测试，评价高性能计算集群的浮点计算能力。目前世界前500超算集群榜单（Top500 list），就是按照HPL的结果进行的测试。

浮点计算峰值是指计算机每秒可以完成的浮点计算次数，包括理论浮点峰值和实测浮点峰值。理论浮点峰值是该计算机理论上每秒可以完成的浮点计算次数，主要由CPU的主频决定。理论浮点峰值＝CPU主频×CPU核数×CPU每周期执行浮点运算的次数。

Jack的文章[1]讲述的就是HPL的历史发展，以及未来展望。近年来HPL逐渐随着GPU的发展而走向异构系统化，在GPU加速方面的研究逐渐变得越来越重要。当然在小规模矩阵上的处理，CPU仍然以通讯优势占据主导。但是随着NPU、DCU等针对性异构系统的出现，我认为计算和计算机体系结构会出现更多样的变化。

文章[6]对许多高性能计算应用软件进行了介绍，同时对我国高性能计算的发展进行了回顾与展望。

Jack 也是最早的一批确定BLAS数学库的先驱者。BLAS（basic linear algebra subroutine） 是一系列基本线性代数运算函数的接口标准． 这里的线性代数运算是指例如矢量的线性组合。BLAS 被广泛用于科学计算和工业界。在更高级的语言和库中，即使我们不直接使用 BLAS 接口，它们也是通过调用 BLAS 来实现的（如 Matlab 中的各种矩阵运算）。

Jack 的实验室写出了第一个BLAS：Lapack。它是用该死的Fortran写的，但是如今我们可以看到这玩意还活跃于MKL等等当中。

Jack还是最早定义了MPI标准的一群人，他对于整个高性能计算领域是非常伟大的贡献，另一个伟大贡献人物是发明超算机的Cray（当然还有一个伟大的人物是李卓钊老师）。Jack Dongarra由于他的突出贡献，在2021年获得了计算机图灵奖。文章[20]讲述了他非凡的生平。

Part 8: 总结                  Chapter 8: Inglourious Basterds

我们对矩阵乘法以及OpenBLAS、MKL进行了一定的测量和研究。我们造出了自己的SGEMM算法，并在一定程度上接近于这两个数学库。但是数学库的庞大让我们明白，我们还有很长很多的路要走。同样的，对底层的学习，对新GPU的学习，我还要走很远。CPU跟GPU都是一群无耻混蛋，对此我们必须喊出我们队的口号：

---

“任何算力，终将被绳之以法！”

---

完蛋！我被超算包围了！——ASC24 南科大超算队_哔哩哔哩_bilibili

Reference

[1] Dongarra, J.J., Luszczek, P., & Petitet, A. (2003). The LINPACK Benchmark: past, present and future. Concurrency and Computation: Practice and Experience, 15. Available: https://netlib.org/utk/people/JackDongarra/PAPERS/hplpaper.pdf

[2] 黎雷生, 杨文浩, 马文静, 张娅, 赵慧, 赵海涛, 李会元, 孙家昶. 复杂异构计算系统HPL的优化. 软件学报, 2021, 32(8): 2307-2318. http://www.jos.org.cn/1000-9825/6003.htm

[3] 水超洋, 于献智, 王银山, 谭光明. 国产异构系统上HPL的优化与分析. 软件学报, 2021, 32(8): 2319-2328. http://www.jos.org.cn/1000-9825/6004.htm

[4] 蔡雨, 孙成国, 杜朝晖, 刘子行, 康梦博, 李双双. 异构HPL算法中CPU端高性能BLAS库优化. 软件学报, 2021, 32(8): 2289-2306. http://www.jos.org.cn/1000-9825/6002.htm

[5] 孙乔,孙家昶,马文静,赵玉文.面向异构计算机平台的HPL方案.软件学报,2021,32(8):2329-2340

[6] 徐顺, 王武, 张鉴, 姜金荣, 金钟, 迟学斌. 面向异构计算的高性能计算算法与软件. 软件学报, 2021, 32(8): 2365-2376. http://www.jos.org.cn/1000-9825/6008.htm

[7] Ma ZX, Jin YY, Tang SZet al. Unified programming models for heterogeneous high-performance computers. JOURNAL OF COMPUTER SCIENCE AND TECHNOLOGY 38(1): 211−218 Jan. 2023. DOI: 10.1007/s11390-023-2888-4

[8] 刘芳芳, 王志军, 汪荃, 吴丽鑫, 马文静, 杨超, 孙家昶. 国产异构系统上的HPCG并行算法及高效实现. 软件学报, 2021, 32(8): 2341-2351. http://www.jos.org.cn/1000-9825/6006.htm

[9] R. C. Whaley and J. J. Dongarra, "Automatically Tuned Linear Algebra Software," SC '98: Proceedings of the 1998 ACM/IEEE Conference on Supercomputing, Orlando, FL, USA, 1998, pp. 38-38, doi: 10.1109/SC.1998.10004.

[10] N. Chalmers, J. Kurzak, D. McDougall and P. T. Bauman, "Optimizing High-Performance Linpack for Exascale Accelerated Architectures," SC23: International Conference for High Performance Computing, Networking, Storage and Analysis, Denver, CO, USA, 2023, pp. 1-12, doi: 10.1145/3581784.3607066.

[11] NVIDIA A100 Tensor Core GPU Architecture 架构白皮书, Available: https://images.nvidia.cn/aem-dam/en-zz/Solutions/data-center/nvidia-ampere-architecture-whitepaper.pdf

[12] NVIDIA Geforce RTX Turing 架构白皮书, Available: https://www.nvidia.cn/geforce/news/geforce-rtx-20-series-turing-architecture-whitepaper/

[13] OpenMP 4.5 API C/C++ Syntax Reference Guide, Available: https://www.openmp.org/wp-content/uploads/OpenMP-4.5-1115-CPP-web.pdf

[14] How to optimize DGEMM on x86 CPU platforms, Available: https://github.com/yzhaiustc/Optimizing-DGEMM-on-Intel-CPUs-with-AVX512F

[15] Intel® Math Kernel Library Improved Small Matrix Performance Using Just-in-Time (JIT) Code Generation for Matrix Multiplication (GEMM), Available: https://www.intel.com/content/www/us/en/developer/articles/technical/onemkl-improved-small-matrix-performance-using-just-in-time-jit-code.html

[16] 齐鲁工业大学 ASC24 OpenCAEPoro 团队&个人优化方案. 黄皮耗子blog: https://blog.sethome.cc/post/asc24-opencaeporo-ge-ren-andtuan-dui-you-hua-fang-an/

[17] J. Choquette, W. Gandhi, O. Giroux, N. Stam and R. Krashinsky, "NVIDIA A100 Tensor Core GPU: Performance and Innovation," in IEEE Micro, vol. 41, no. 2, pp. 29-35, 1 March-April 2021, doi: 10.1109/MM.2021.3061394.

[18] Abstract: NVIDIA A100 Tensor Core GPU is NVIDIA's latest flagship GPU.URL: https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=9361255&isnumber=9388768

[19] 國立清華大學開放式課程 10701 平行程式 周志遠 教授 Available: https://ocw.nthu.edu.tw/ocw/index.php?page=chapter&cid=231&chid=2574&video_url=https%3A%2F%2Focw.nthu.edu.tw%2Fvideosite%2Findex.php%3Fop%3Dwatch%26id%3D7625%26filename%3D1920_1080_3072.MP4%26type%3Dview%26cid%3D231%26chid%3D2574&name=L1A

[20] The Influence and Contribution of Jack Dongarra to Numerical Linear Algebra https://hammarling.com/sven/pubs/HaHi22_Final.pdf

[21] J. Langou, J. Langou, P. Luszczek, J. Kurzak, A. Buttari and J. Dongarra, "Exploiting the Performance of 32 bit Floating Point Arithmetic in Obtaining 64 bit Accuracy (Revisiting Iterative Refinement for Linear Systems)," SC '06: Proceedings of the 2006 ACM/IEEE Conference on Supercomputing, Tampa, FL, USA, 2006, pp. 50-50, doi: 10.1109/SC.2006.30.

[22] A. Abdelfattah, M. Baboulin, V. Dobrev, J. Dongarra, C. Earl, J. Falcou, A. Haidar, I. Karlin, Tz. Kolev, I. Masliah, S. Tomov, High-performance Tensor Contractions for GPUs, Procedia Computer Science, Volume 80, 2016, Pages 108-118, ISSN 1877-0509, https://doi.org/10.1016/j.procs.2016.05.302.

[23] J. Dongarra, High-Performance Matrix-Matrix Multiplications of Very Small Matrices, https://netlib.org/utk/people/JackDongarra//PAPERS/high-performance-matrix-matrix.pdf

[24] 南科大科学与工程计算中心超级计算机用户手册(启明2.0和太乙) https://hpc.sustech.edu.cn/ref/cluster_User_Manual.pdf

[25] 2023年南科大科学与工程计算中心年报 https://hpc.sustech.edu.cn/ref/2023CCSEAnnualReport.pdf

[26] BLAS Quick Reference Guide, Available: https://www.netlib.org/blas/blasqr.pdf

[27] Brehob, Mark & Enbody, R.J.. An analytical model of locality and caching. https://www.researchgate.net/publication/228814140_An_analytical_model_of_locality_and_caching/figures?lo=1&utm_source=bing&utm_medium=organic

[28] 刘昊,刘芳芳,张鹏,杨超,蒋丽娟.基于申威1600的3级BLAS GEMM函数优化.计算机系统应用,2016,25(12):234-239 http://www.c-s-a.org.cn/csa/article/pdf/20161237

[29] 殷顺昌. OpenMP并行程序性能分析[D].国防科学技术大学,2007.

[30] 高雨辰. 面向国产处理器的OpenMP程序编译优化技术研究[D].战略支援部队信息工程大学,2019.

[31] Smith, T.M., & van de Geijn, R.A. (2017). A Tight I/O Lower Bound for Matrix Multiplication. ACM Transactions on Mathematical Software (TOMS). https://arxiv.org/pdf/1702.02017

Appendix

 可以学习这两篇文章介绍PCIe3：https://zhuanlan.zhihu.com/p/639722704  https://zhuanlan.zhihu.com/p/454282470

 GPU的小科普 https://zhuanlan.zhihu.com/p/406572255

 GPU架构介绍 https://zhuanlan.zhihu.com/p/423129242

EOF