Compiler 3: NFA, DFA, CFG
- 编译原理
- 2025-09-25
- 18热度
- 0评论
第一章最后一部分+CFG
Convert NFA to DFA
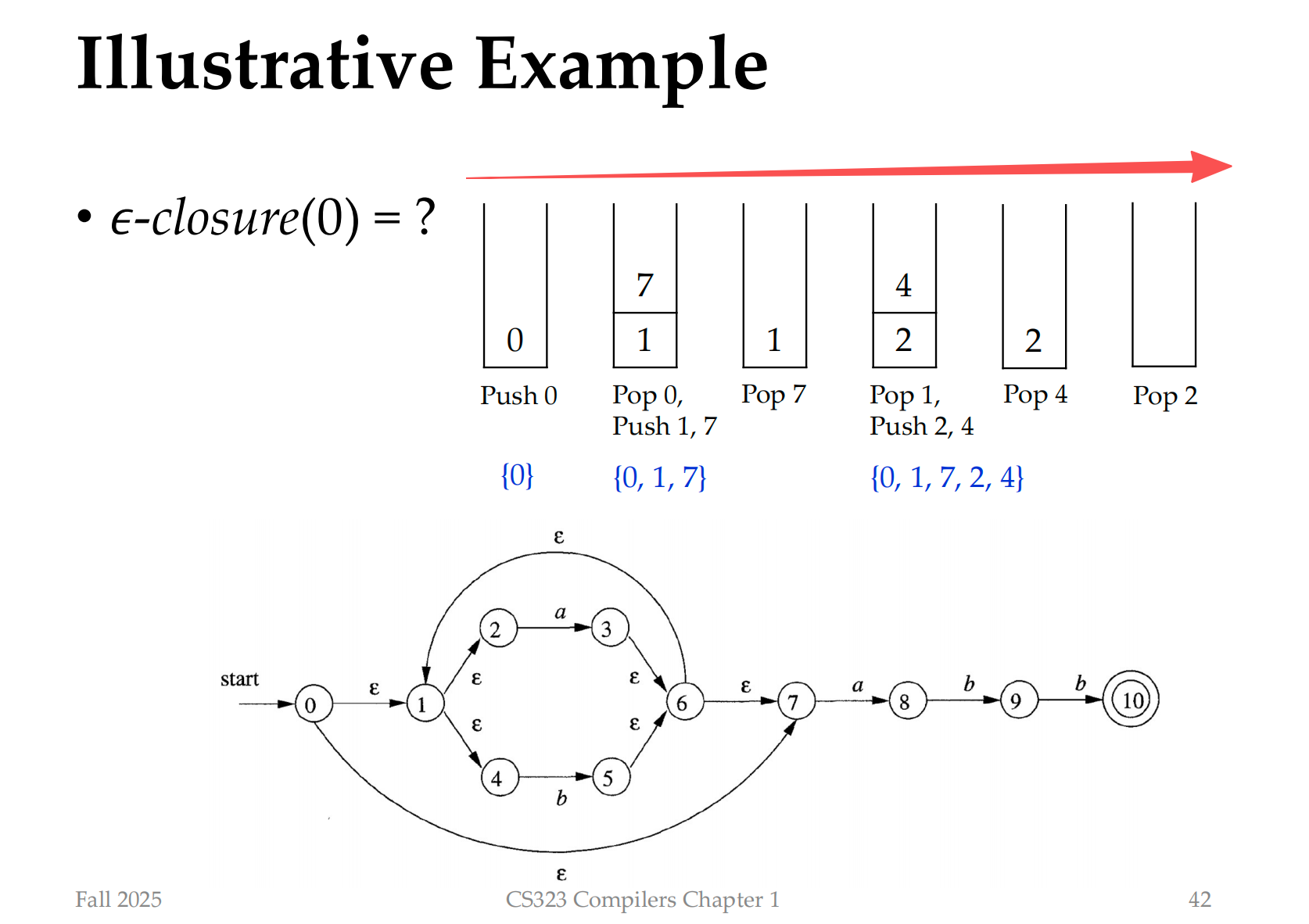
The algorithm here is to explore the state
[1,2,3,4,6,7,8] 是在move[A,a]后能达到的所有状态
![[Pasted image 20250921142734.png]]
我们用达到闭包的个数，来判定目前的状态
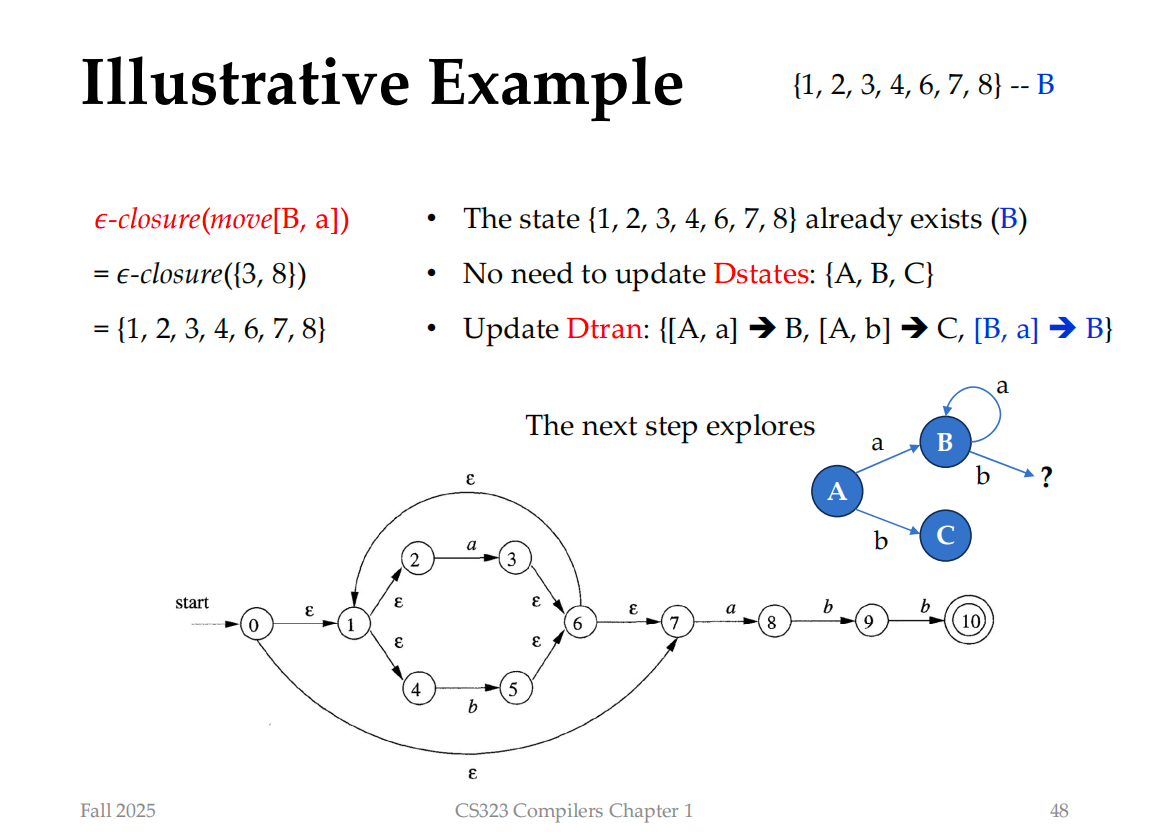
Start State A (We have 0), Accepting States E (We have 10)
这样，我们就能找到一个DFA，其每一个输入，都会对应一个状态
Regexp -> NFA
We can now construct a machine to recognize "s|t"
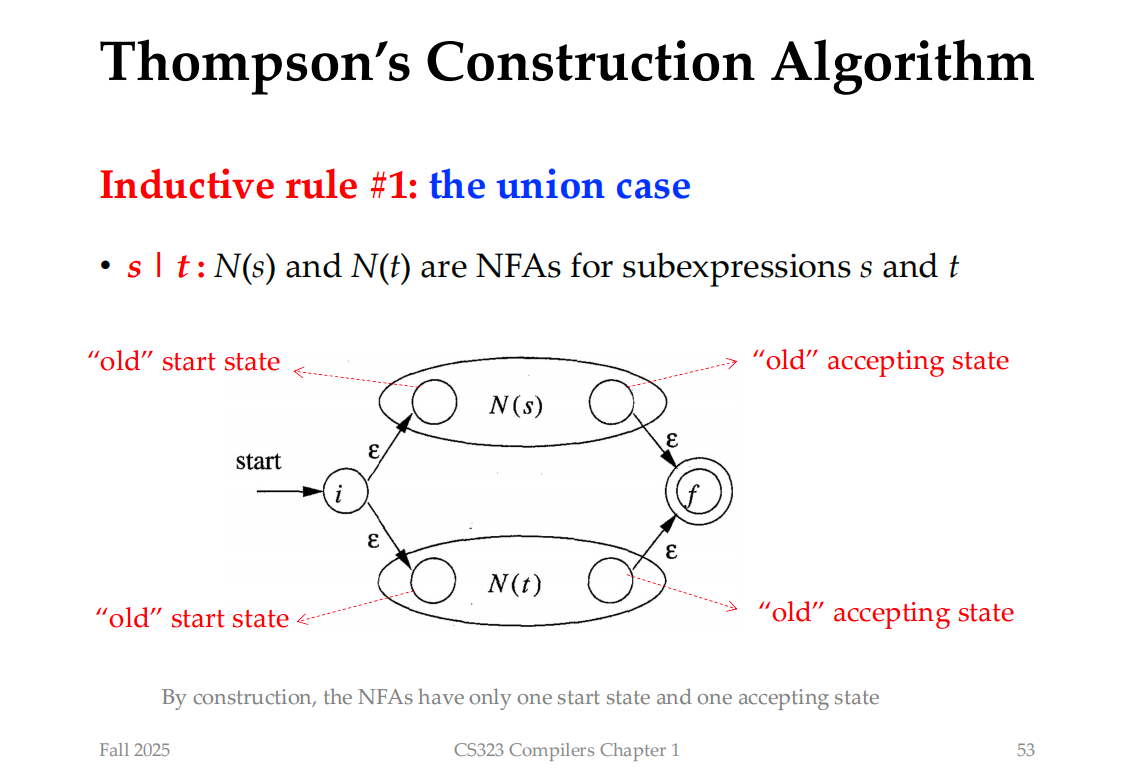
How to represent "st", use an intermediate state:
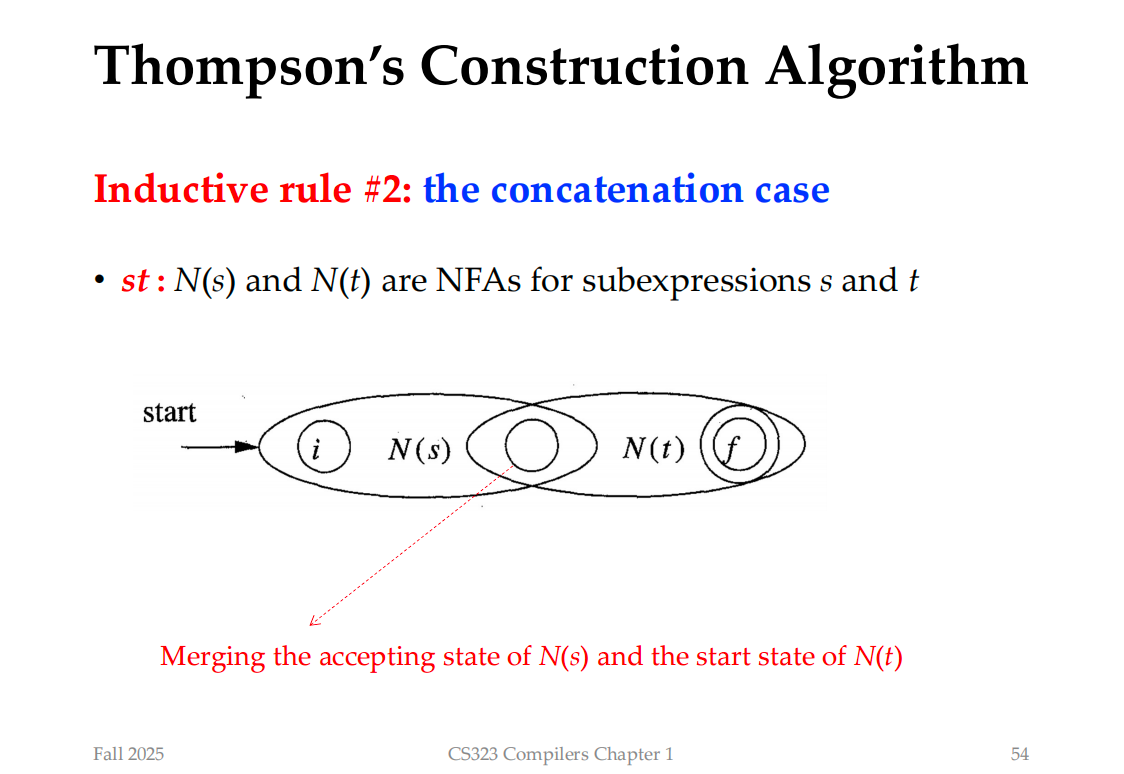
Kleene: 返回即可， s*
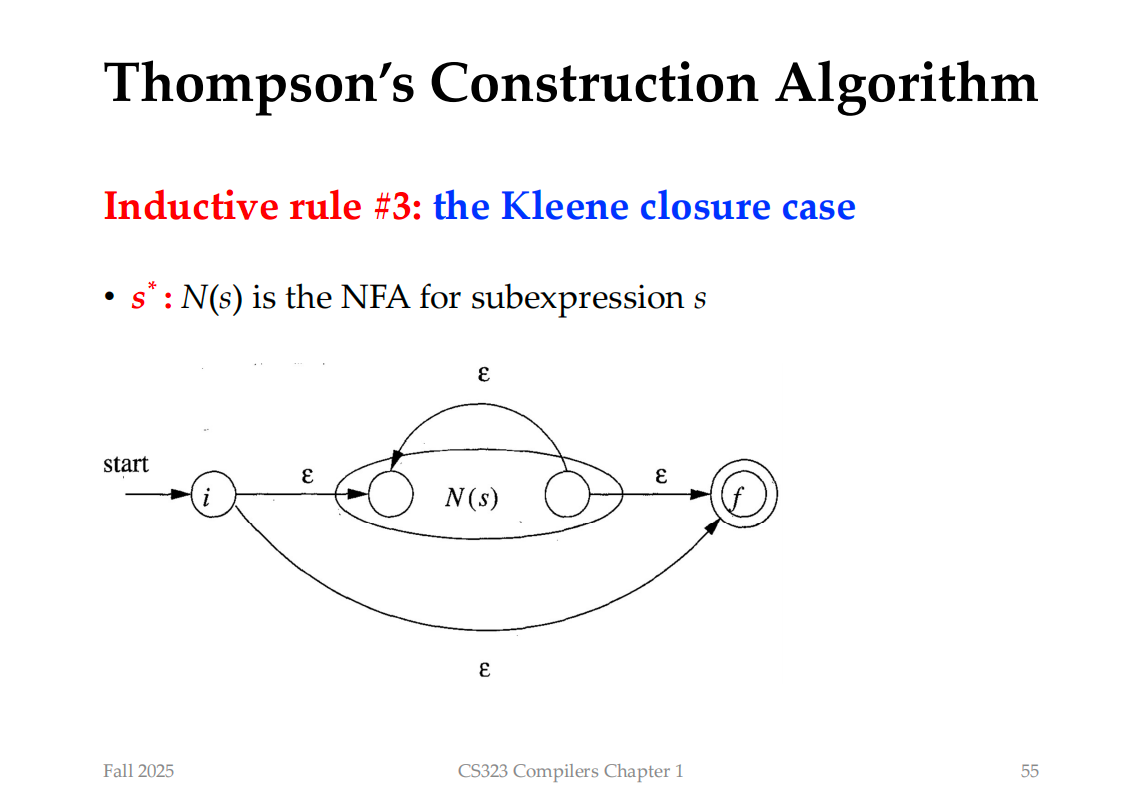
Example
神奇的是，我们应该先构造子表达式，再构造顶层式子
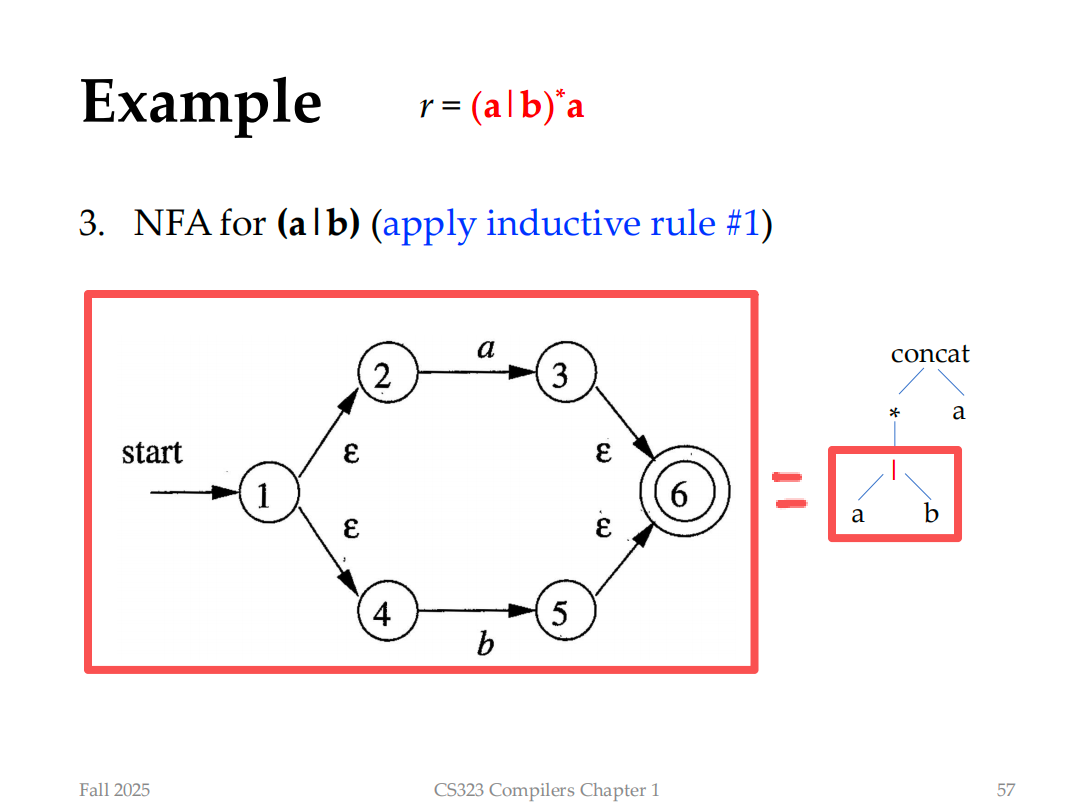
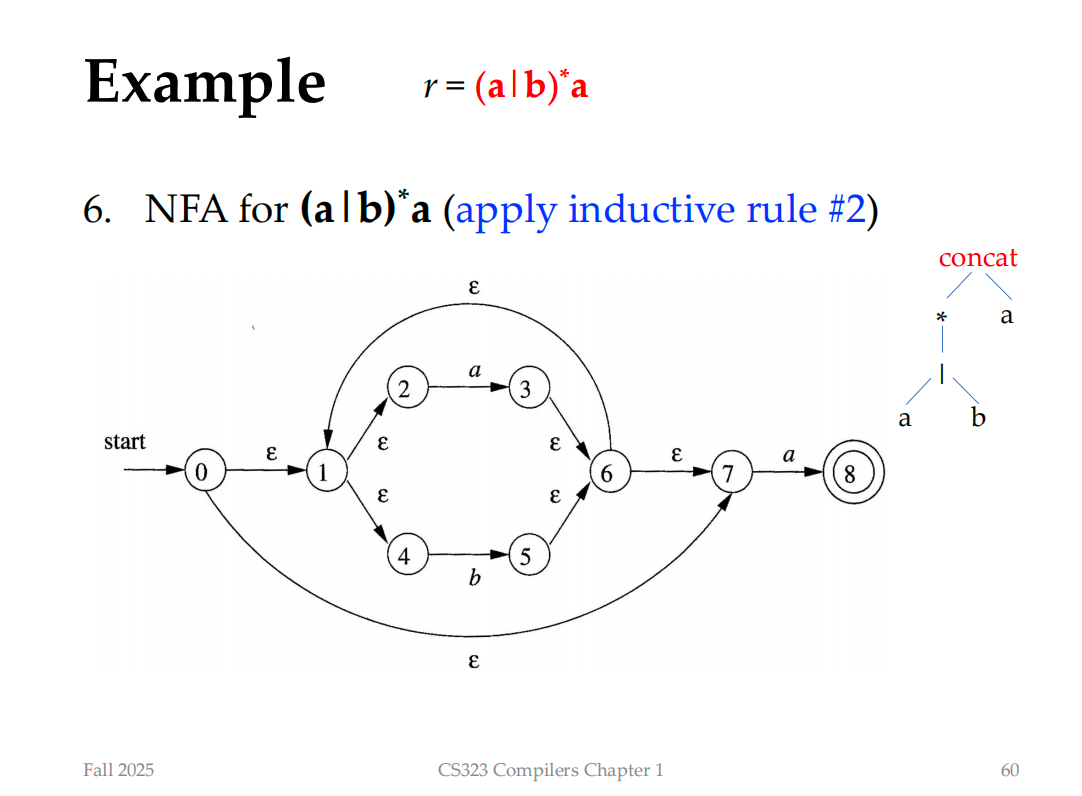
Finite Automata
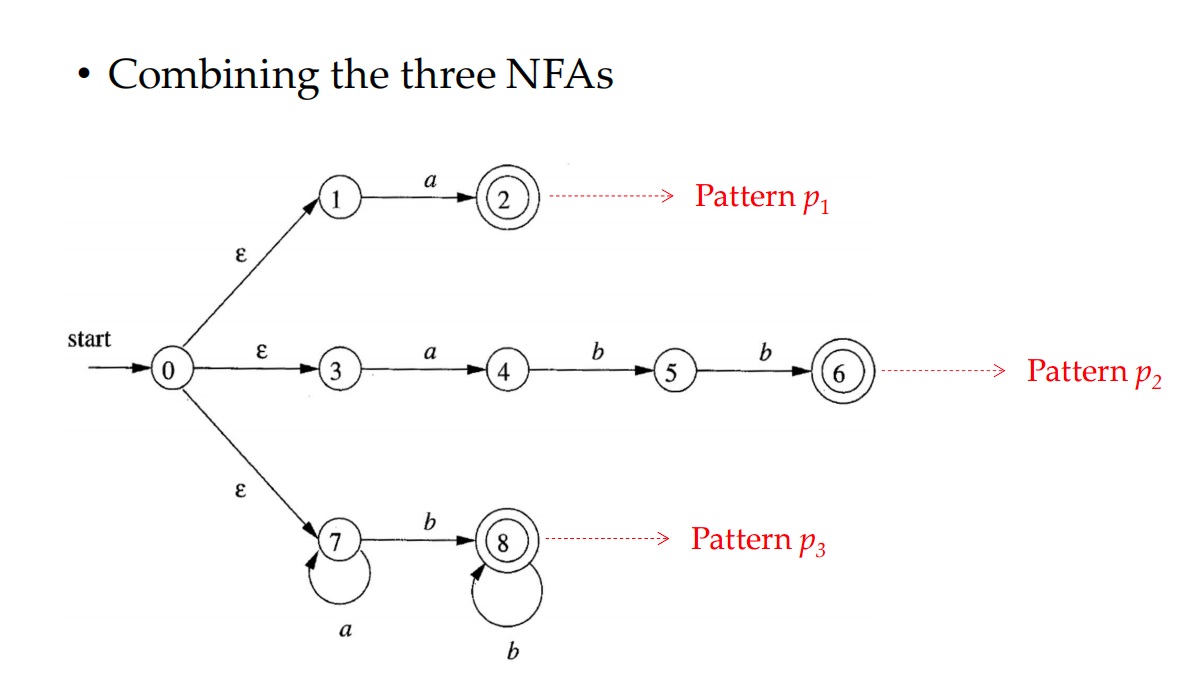
Combining NFAs
In Lexical Analyzer, we will get many regular expression for different pattern
And we can do: Regexp -> NFA
And we combine these NFAs using an union like combination
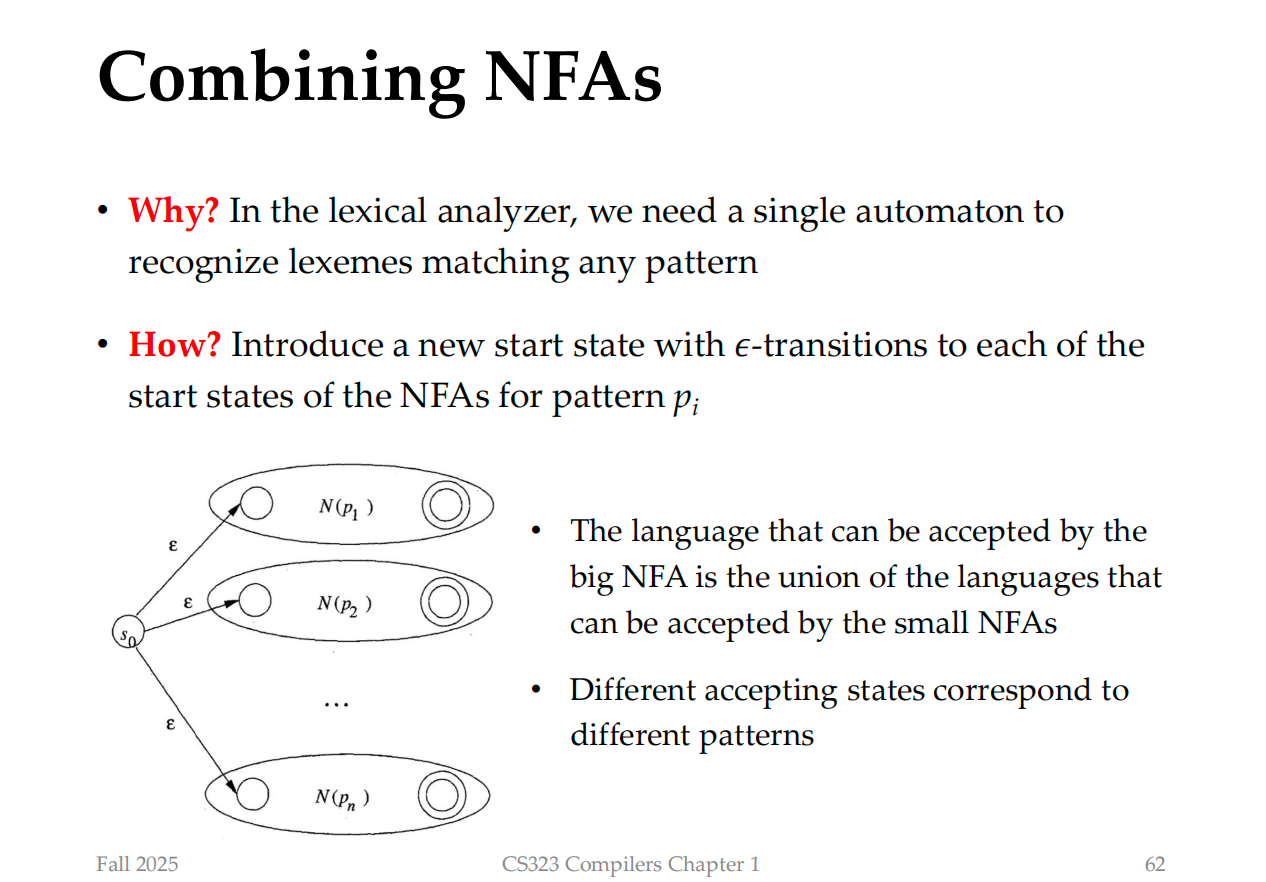
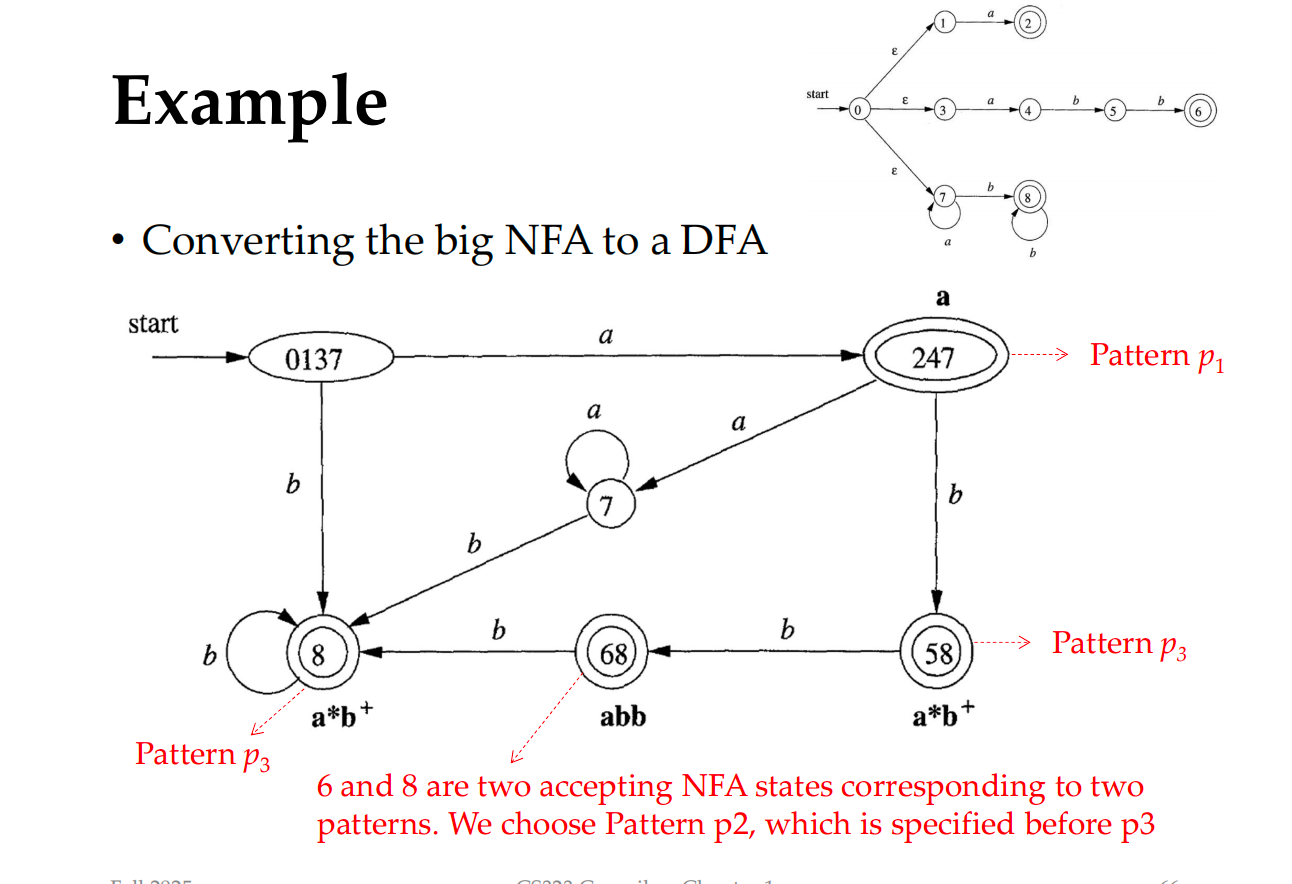
Then for each NFA, convert them into DFA
Example
a {action A1 for pattern p1 }
abb {action A2 for pattern p2 }
a*b+ {p3}
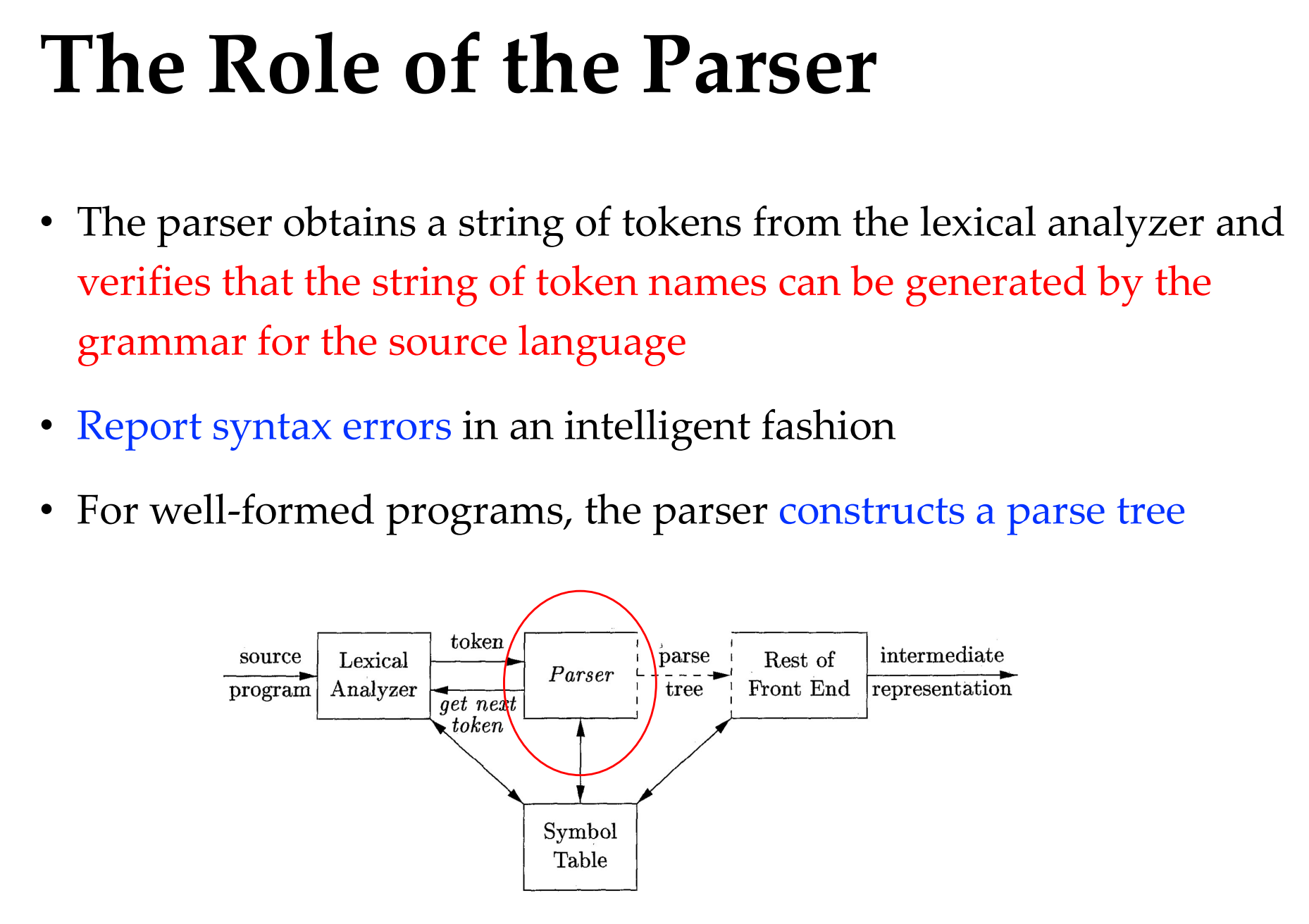
Context-Free Grammars && Syntax Analysis
To see if we have syntax error
例子：a+b
expression 可以是 expression + term
expression 可以是 term
term 可以是factor
factor可以是id
所以这个产生式可以产生 a+b
推导 (Derivation)
-
推导：从 开始符号 (Start Symbol) 出发，不断使用产生式 (Production Rules) 替换非终结符 (Nonterminals)，直到得到一个只包含 终结符 (Terminals) 的串。
-
最终得到的串就是属于该文法的一个 句子 (Sentence)。
换句话说，推导就是一个逐步 展开 的过程，把抽象的语法规则一步步替换成具体的符号，直到得到实际的程序片段或字符串。
2. 推导的形式
如果我们有文法规则：
Expr → Expr + Term | Term
Term → Term * Factor | Factor
Factor → ( Expr ) | id-
开始符号：
Expr -
推导过程（一个例子）：
Expr ⇒ Expr + Term （应用 Expr → Expr + Term） ⇒ Term + Term （应用 Expr → Term） ⇒ Factor + Term （应用 Term → Factor） ⇒ id + Term （应用 Factor → id） ⇒ id + Factor （应用 Term → Factor） ⇒ id + id （应用 Factor → id） -
得到的句子：
id + id
3. 两种常见推导方式
-
左推导 (Leftmost Derivation)：每一步都替换最左边的非终结符。
-
右推导 (Rightmost Derivation)：每一步都替换最右边的非终结符。
上面例子就是一个左推导。
不同推导方式得到的最终结果一样，但中间步骤不同。
4. 与语法树的关系
- 推导过程可以用 推导树 (Derivation Tree / Parse Tree) 来表示。
- 推导描述了“展开的过程”，语法树描述了“最终的结构”。
👉 总结：
Derivation = 从开始符号出发，用产生式一步步替换非终结符，直到只剩终结符。
它解释了一个字符串是如何根据 CFG 被“生成”的。
要不要我帮你画一个 id + id 的推导树 (Parse Tree)，让你直观理解 Derivation 和语法树的关系？