Pytorch ATen Matmul CPU 算子解析
- Frameworks
- 2025-06-12
- 885 Views
- 0 Comments
- 2411 Words
在上一期 https://www.haibinlaiblog.top/index.php/llm-on-cpu/ , 我们探讨了各个LLM的具体结构,今天我们就来探寻这些结构/算子的底层实现。
上一期我们探讨的架构:LLM各阶段的代码在pytorch的实现
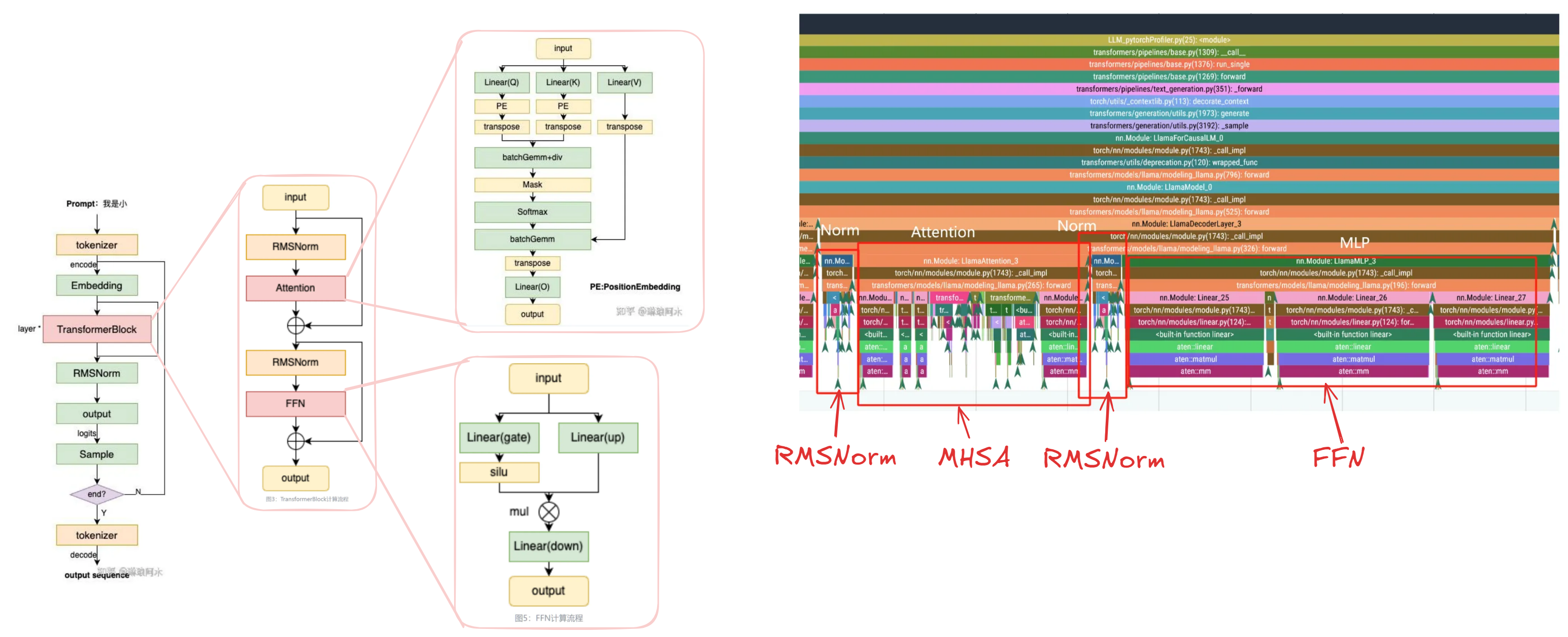
Pytorch调用栈解析
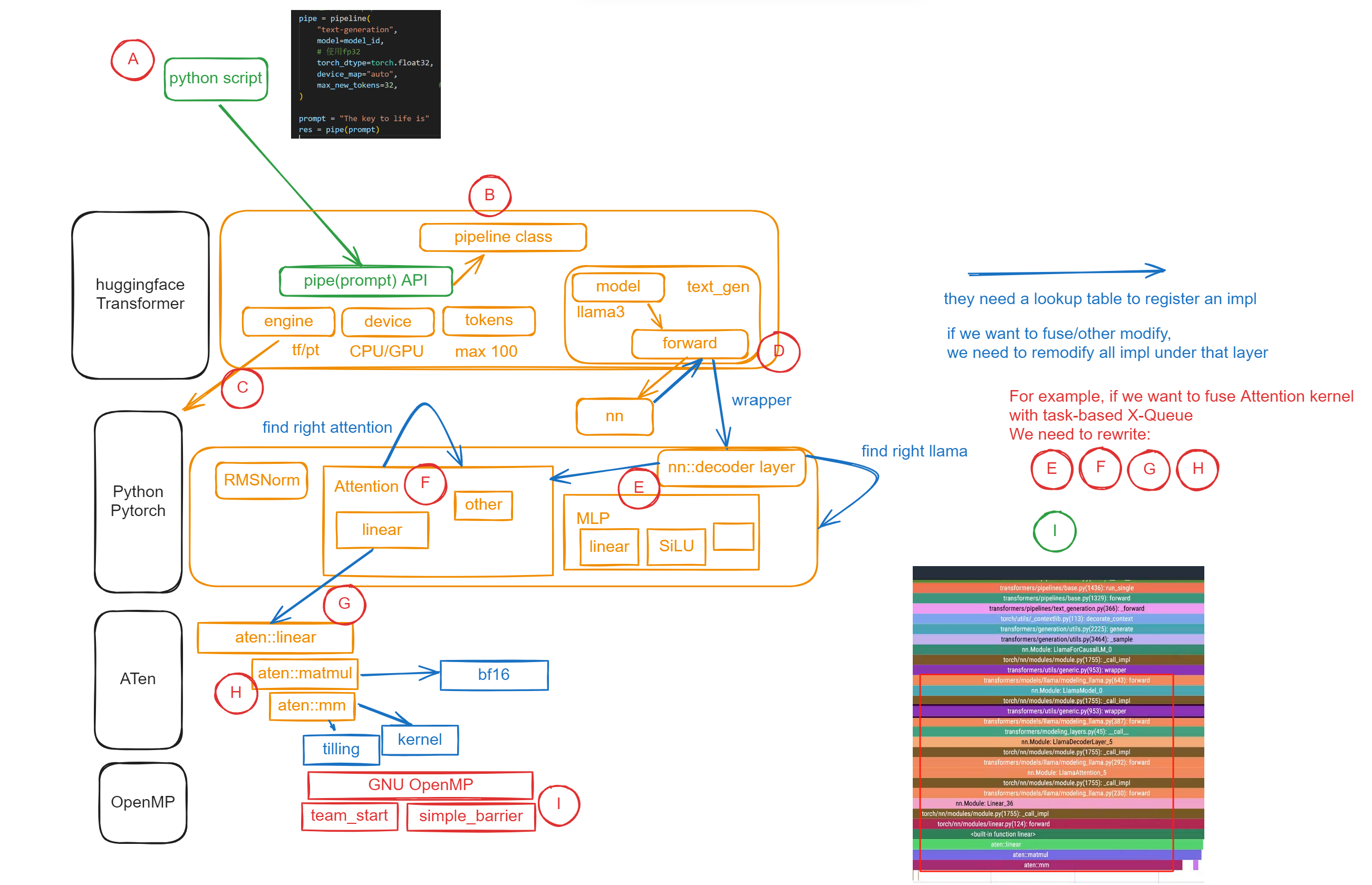
所以你这边就能看到Pytorch的调用核心逻辑了。它会先决定做什么算子,什么数据。然后回call_impl,此时它会根据之前的config(比如用GPU还是CPU,有多少线程/SM),然后调用具体的一个底层实现。
引用一句话:
要学习ATen其实非常简单,在aten目录里面乱扒乱翻一通,挨个文件夹都点开瞅两眼,把所有的README.md都读一遍,就会发现,实际上ATen的算符是怎么定义的,实际上,已经在aten/src/ATen/README.md文件中,进行了非常详细的说明。
PyTorch C++ API — PyTorch main documentation
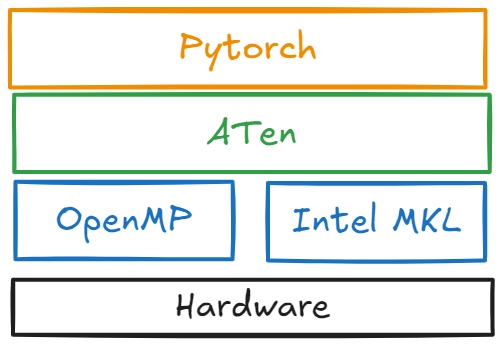
• ATen: The foundational tensor and mathematical operation library on which all else is built.
ATen is fundamentally a tensor library, on top of which almost all other Python and C++ interfaces in PyTorch are built. It provides a core Tensor class, on which many hundreds of operations are defined. Most of these operations have both CPU and GPU implementations, to which the Tensor class will dynamically dispatch based on its type. A small example of using ATen could look as follows:
huggingface example:
import torch
from transformers import pipeline
import time
model_id = "meta-llama/Llama-3.2-1B"
torch.manual_seed(123)
pipe = pipeline(
"text-generation",
model=model_id,
torch_dtype=torch.bfloat16,
device_map="auto",
max_new_tokens=256,
)
start = time.time()
res = pipe("The key to life is")ATen Matmul 解析
/*
Matrix product of two Tensors.
The behavior depends on the dimensionality of the Tensors as follows:
- If both Tensors are 1-dimensional, the dot product (scalar) is returned.
- If both arguments are 2-dimensional, the matrix-matrix product is returned.
- If the first argument is 1-dimensional and the second argument is 2-dimensional,
a 1 is prepended to its dimension for the purpose of the matrix multiply.
After the matrix multiply, the prepended dimension is removed.
- If the first argument is 2-dimensional and the second argument is 1-dimensional,
the matrix-vector product is returned.
- If both arguments are at least 1-dimensional and at least one argument is
N-dimensional (where N > 2), then a batched matrix multiply is returned. If the first
argument is 1-dimensional, a 1 is prepended to its dimension for the purpose of the
batched matrix multiply and removed after. If the second argument is 1-dimensional, a
1 is appended to its dimension for the purpose of the batched matrix multiple and removed after.
The non-matrix (i.e. batch) dimensions are broadcasted (and thus
must be broadcastable). For example, if tensor1 is a (j x 1 x n x m) Tensor
and tensor2 is a (k x m x p) Tensor, the returned tensor will be an (j x k x n x p) Tensor.
*/
Tensor matmul(const Tensor & tensor1, const Tensor & tensor2) {
auto dim_tensor1 = tensor1.dim();
auto dim_tensor2 = tensor2.dim();
if (dim_tensor1 == 1 && dim_tensor2 == 1) {
return tensor1.dot(tensor2);
} else if (dim_tensor1 == 2 && dim_tensor2 == 1) {
return tensor1.mv(tensor2);
} else if (dim_tensor1 == 1 && dim_tensor2 == 2) {
return tensor1.unsqueeze(0).mm(tensor2).squeeze_(0);
} else if (dim_tensor1 == 2 && dim_tensor2 == 2) {
return tensor1.mm(tensor2);
} else if (dim_tensor1 >= 3 && (dim_tensor2 == 1 || dim_tensor2 == 2)) {
// optimization: use mm instead of bmm by folding tensor1's batch into
// its leading matrix dimension.
Tensor t2 = dim_tensor2 == 1 ? tensor2.unsqueeze(-1) : tensor2;
auto size1 = tensor1.sizes();
auto size2 = t2.sizes();
std::vector<int64_t> output_size;
output_size.insert(output_size.end(), size1.begin(), size1.end() - 1);
output_size.insert(output_size.end(), size2.end() - 1, size2.end());
// fold the batch into the first dimension
Tensor t1 = tensor1.contiguous().view({-1, size1[size1.size() - 1]});
auto output = t1.mm(t2).view(output_size);
if (dim_tensor2 == 1) {
output = output.squeeze(-1);
}
return output;
} else if ((dim_tensor1 >= 1 && dim_tensor2 >= 1) && (dim_tensor1 >= 3 || dim_tensor2 >= 3)) {
// We are multiplying b1 x n x m1 by x2 x m2 x p (where b1 can be a list);
// we track m1 vs m2 separately even though they must match for nicer error messages
int64_t n = dim_tensor1 > 1 ? tensor1.size(-2) : 1;
int64_t m1 = tensor1.size(-1);
IntList batch_tensor1(tensor1.sizes().data(), std::max<int64_t>(dim_tensor1 - 2, 0));
int64_t m2 = dim_tensor2 > 1 ? tensor2.size(-2) : 1;
int64_t p = tensor2.size(-1);
IntList batch_tensor2(tensor2.sizes().data(), std::max<int64_t>(dim_tensor2 - 2, 0));
// expand the batch portion (i.e. cut off matrix dimensions and expand rest)
std::vector<int64_t> expand_batch_portion = infer_size(batch_tensor1, batch_tensor2);
std::vector<int64_t> tensor1_expand_size(expand_batch_portion);
tensor1_expand_size.insert(tensor1_expand_size.end(), {n, m1});
std::vector<int64_t> tensor2_expand_size(expand_batch_portion);
tensor2_expand_size.insert(tensor2_expand_size.end(), {m2, p});
int expand_batch_product = std::accumulate(expand_batch_portion.begin(), expand_batch_portion.end(),
1, std::multiplies<int64_t>());
std::vector<int64_t> tensor1_bmm_view({expand_batch_product});
tensor1_bmm_view.insert(tensor1_bmm_view.end(), {n, m1});
std::vector<int64_t> tensor2_bmm_view({expand_batch_product});
tensor2_bmm_view.insert(tensor2_bmm_view.end(), {m2, p});
// flatten expanded batches
Tensor tensor1_expanded = tensor1.expand(tensor1_expand_size).contiguous().view(tensor1_bmm_view);
Tensor tensor2_expanded = tensor2.expand(tensor2_expand_size).contiguous().view(tensor2_bmm_view);
Tensor output = tensor1_expanded.bmm(tensor2_expanded);
// reshape batches back into result
std::vector<int64_t> total_expansion(expand_batch_portion);
total_expansion.insert(total_expansion.end(), {n, p});
return maybeSqueeze(output.view(total_expansion), dim_tensor1, dim_tensor2);
}
runtime_error("both arguments to matmul need to be at least 1D, but they are %dD and %dD",
dim_tensor1, dim_tensor2);
}是的,这段代码是 PyTorch (ATen) 中实现 matmul 操作的一部分,用于处理各种维度下的张量矩阵乘法。这是 torch.matmul() 的底层 C++ 实现,它通过判断输入张量维度的组合情况,选择对应的乘法逻辑并进行必要的维度扩展、变形等处理。
📌 主要逻辑简述:
这个函数根据两个输入 tensor1 和 tensor2 的维度组合,选择不同的矩阵乘法策略:
✅ 1. 一维 × 一维(向量点积):
if (dim_tensor1 == 1 && dim_tensor2 == 1)
return tensor1.dot(tensor2);tensor1.shape = (N),tensor2.shape = (N)-
返回一个标量(dot product)。
✅ 2. 二维 × 一维(矩阵-向量乘):
else if (dim_tensor1 == 2 && dim_tensor2 == 1) return tensor1.mv(tensor2); tensor1.shape = (M, N),tensor2.shape = (N)- 返回
(M)向量。
✅ 3. 一维 × 二维(向量 × 矩阵):
else if (dim_tensor1 == 1 && dim_tensor2 == 2)
return tensor1.unsqueeze(0).mm(tensor2).squeeze_(0);tensor1.shape = (N),tensor2.shape = (N, P)-
添加 batch 维
(1, N),进行乘法后 squeeze 得到(P)。✅ 4. 二维 × 二维(普通矩阵乘法):
else if (dim_tensor1 == 2 && dim_tensor2 == 2) return tensor1.mm(tensor2); tensor1.shape = (M, N),tensor2.shape = (N, P)-
返回
(M, P)。✅ 5. 高维 × 一维/二维(优化路径,使用 mm 而非 bmm):
else if (dim_tensor1 >= 3 && (dim_tensor2 == 1 || dim_tensor2 == 2)) { ... // batch 折叠成第一维,使用 mm 而不是 bmm } - 将
tensor1的前几维 flatten 成 batch,再用mm计算,后 reshape。 -
比如
tensor1: (B1 x B2 x N x M),tensor2: (M)→ flatten 成(B1*B2, N, M),计算后 reshape 回(B1, B2, N)。✅ 6. 通用的 batched matmul(高维广播+批量 bmm):
else if ((dim_tensor1 >= 1 && dim_tensor2 >= 1) && (dim_tensor1 >= 3 || dim_tensor2 >= 3)) { ... // 广播 + 展平 + bmm + reshape }🚩主要处理:
- 对 batch 维(除最后两个维度)进行广播。
- 张量 reshape 成
(B, N, M)和(B, M, P),用bmm计算。 -
然后 reshape 成
(batch_dims..., N, P)。✅ 7. 错误处理:
runtime_error("both arguments to matmul need to be at least 1D..."); - 如果两个张量维度都小于 1,报错。
💡小结:这个函数做了什么?
它是 torch.matmul() 在 ATen 层的 多维泛化实现,核心职责是:
- 判断输入张量的维度模式;
- 自动扩展维度(如 unsqueeze);
- 自动广播 batch 维;
- 选择合适的底层乘法函数(dot, mv, mm, bmm);
- 在乘法前后 reshape 或 squeeze 以满足输出维度预期;
- 提供错误提示。
ATen 底层计算方法
#if COMPILER_SUPPORTS_BF16_TARGET
TARGET_ARM_BF16_ATTRIBUTE float
dot_with_fp32_arith_bfdot(const BFloat16* vec1, const BFloat16* vec2, int64_t len) {
auto reduced_sum = dot_with_fp32_arith_main_loop_bfdot(vec1, vec2, len);
DOT_WITH_FP32_ARITH_TAIL_AFTER_MAIN_LOOP_BODY(_bfdot);
}
#endif // COMPILER_SUPPORTS_BF16_TARGET
float bf16_dot_with_fp32_arith(const at::BFloat16* vec1, const at::BFloat16* vec2, int64_t len) {
#if COMPILER_SUPPORTS_BF16_TARGET
if (cpuinfo_has_arm_bf16()) {
return dot_with_fp32_arith_bfdot(vec1, vec2, len);
} else
#endif // COMPILER_SUPPORTS_BF16_TARGET
{
return dot_with_fp32_arith_no_bfdot(vec1, vec2, len);
}
}
C10_ALWAYS_INLINE TARGET_ARM_BF16_ATTRIBUTE auto
dot_with_fp32_arith_main_loop_bfdot(
const BFloat16* vec1,
const BFloat16* vec2,
int64_t len) {
vec::VectorizedN<float, kF32RegistersPerIteration> sum(0);
const auto len_aligned = len & ~(kF32ElementsPerIteration - 1);
for (int j = 0; j < len_aligned ; j += kF32ElementsPerIteration) {
const auto* vec1_ = vec1 + j;
const auto* vec2_ = vec2 + j;
ForcedUnrollTargetBFloat16<kF32RegisterPairsPerIteration>{}([vec1_, vec2_, &sum](auto k)
C10_ALWAYS_INLINE_ATTRIBUTE TARGET_ARM_BF16_ATTRIBUTE {
dot_with_fp32_arith_main_inner_loop_bfdot(vec1_, vec2_, sum, k);
});
}
return reduce(sum);
}
#endif // COMPILER_SUPPORTS_BF16_TARGET
TARGET_ARM_BF16_ATTRIBUTE C10_ALWAYS_INLINE void
dot_with_fp32_arith_main_inner_loop_bfdot(
const BFloat16* vec1,
const BFloat16* vec2,
vec::VectorizedN<float, kF32RegistersPerIteration>& sum,
int registerPairIndex) {
// NOTE[Intrinsics in bfdot variant]: We can't use
// vec::Vectorized<BFloat16>::loadu here because linux-aarch64 GCC
// inexplicably can't convert Vectorized<BFloat16> to
// bfloat16x8_t. I suspect a bug or incomplete
// __attribute__((target)) implementation. Intrinsics should be fine
// because we're using vbfdotq_f32 below anyway.
const auto temp_vec1 = vld1q_bf16(
reinterpret_cast<const bfloat16_t*>(
&vec1[registerPairIndex * vec::Vectorized<BFloat16>::size()]));
const auto temp_vec2 = vld1q_bf16(
reinterpret_cast<const bfloat16_t*>(
&vec2[registerPairIndex * vec::Vectorized<BFloat16>::size()]));
sum[registerPairIndex] =
vbfdotq_f32(sum[registerPairIndex], temp_vec1, temp_vec2);
}
| 内容 | 说明 |
|---|---|
| 操作类型 | BFloat16 向量点积(dot product) |
| 累加精度 | Float32 精度累加(即更高精度累积) |
| 使用硬件指令 | vbfdotq_f32(ARM SIMD BF16 点积指令) |
| 多寄存器处理 | 使用 VectorizedN 同时处理多个寄存器对 |
| 展开策略 | 强制循环展开,减少分支,增强流水 |
template <typename T>
C10_ALWAYS_INLINE float
dot_with_fp32_arith_no_bfdot(const T* vec1, const T* vec2, int64_t len) {
auto reduced_sum = dot_with_fp32_arith_main_loop_no_bfdot(vec1, vec2, len);
DOT_WITH_FP32_ARITH_TAIL_AFTER_MAIN_LOOP_BODY(_no_bfdot);
}
#undef DOT_WITH_FP32_ARITH_TAIL_AFTER_MAIN_LOOP_BODY
float fp16_dot_with_fp32_arith(const Half* vec1, const Half* vec2, int64_t len) {
return dot_with_fp32_arith_no_bfdot(vec1, vec2, len);
}
template <typename T>
C10_ALWAYS_INLINE auto
dot_with_fp32_arith_main_loop_no_bfdot(
const T* vec1,
const T* vec2,
int64_t len) {
vec::VectorizedN<float, kF32RegistersPerIteration> sum(0);
const auto len_aligned = len & ~(kF32ElementsPerIteration - 1);
for (int j = 0; j < len_aligned ; j += kF32ElementsPerIteration) {
const auto* vec1_ = vec1 + j;
const auto* vec2_ = vec2 + j;
c10::ForcedUnroll<kF32RegisterPairsPerIteration>{}([vec1_, vec2_, &sum](auto k) C10_ALWAYS_INLINE_ATTRIBUTE {
dot_with_fp32_arith_main_inner_loop_no_bfdot(vec1_, vec2_, sum, k);
});
}
return reduce(sum);
}那么这里就是ATen 矩阵乘法最低层的实现了。可以看到这里它会导入数据,然后调用一个核心kernel
你可能好奇,那我缺的这个数据谁给我补啊?是这样的,他们会在计算前提前分好数据,然后进行计算
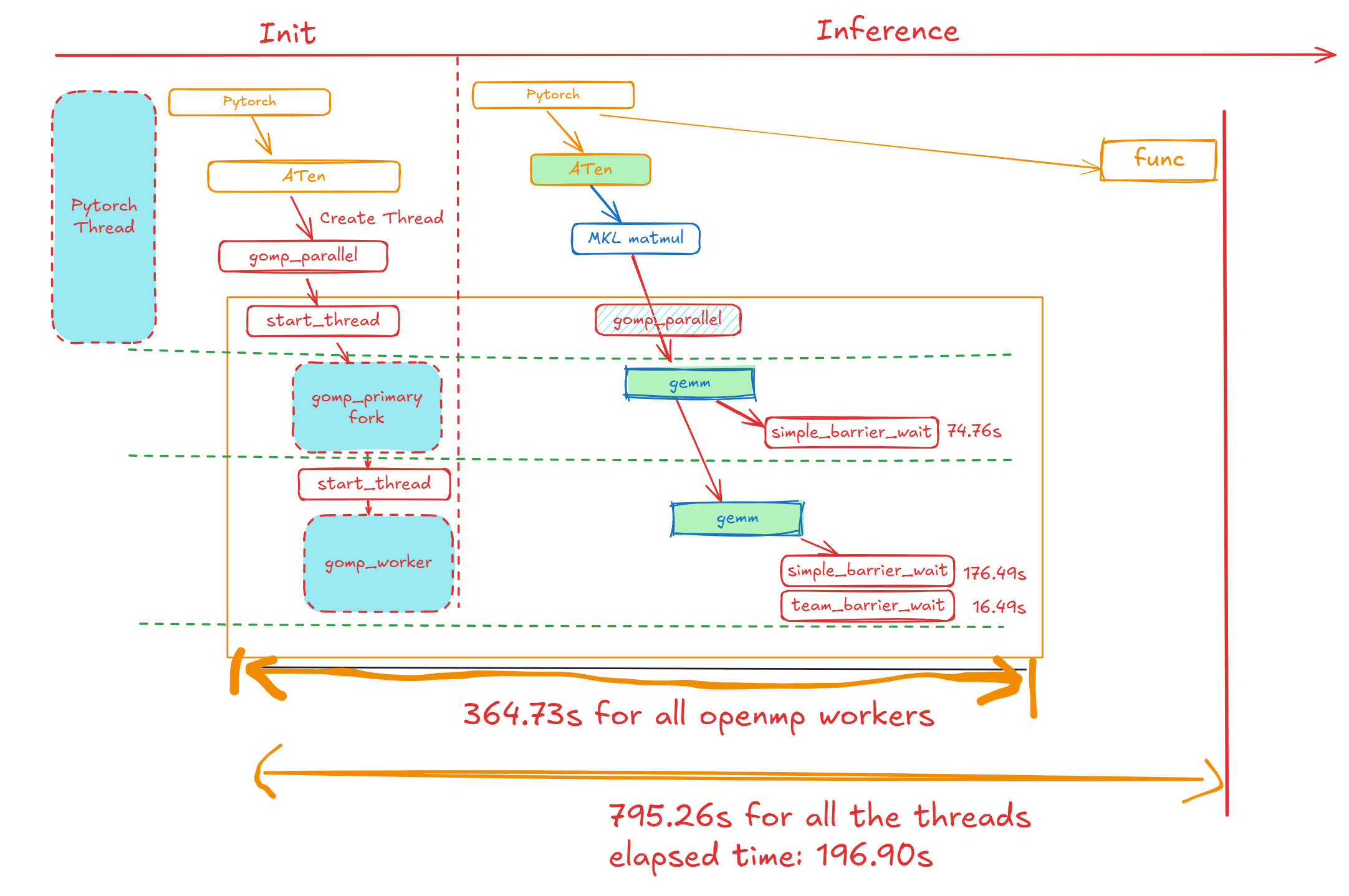
开始并行的代码:Parallel_for
是的,这里就像是OpenMP分配的情况
parallel_for
pytorch/aten/src/ATen/Parallel-inl.h at e3cf73ee4948468b5bd60b03df637f2986c108fd · pytorch/pytorch
template <class F>
inline void parallel_for(
const int64_t begin,
const int64_t end,
const int64_t grain_size,
const F& f) {
TORCH_INTERNAL_ASSERT_DEBUG_ONLY(grain_size >= 0);
if (begin >= end) {
return;
}
#ifdef INTRA_OP_PARALLEL
at::internal::lazy_init_num_threads();
const auto numiter = end - begin;
const bool use_parallel =
(numiter > grain_size && numiter > 1 && !at::in_parallel_region() &&
at::get_num_threads() > 1);
if (!use_parallel) {
internal::ThreadIdGuard tid_guard(0);
c10::ParallelGuard guard(true);
f(begin, end);
return;
}
internal::invoke_parallel(
begin, end, grain_size, [&](int64_t begin, int64_t end) {
c10::ParallelGuard guard(true);
f(begin, end);
});
#else
internal::ThreadIdGuard tid_guard(0);
c10::ParallelGuard guard(true);
f(begin, end);
#endif
}void invoke_parallel(
const int64_t begin,
const int64_t end,
const int64_t grain_size,
const std::function<void(int64_t, int64_t)>& f) {
at::internal::lazy_init_num_threads();
size_t num_tasks = 0, chunk_size = 0;
std::tie(num_tasks, chunk_size) =
internal::calc_num_tasks_and_chunk_size(begin, end, grain_size);
struct {
std::atomic_flag err_flag = ATOMIC_FLAG_INIT;
std::exception_ptr eptr;
std::mutex mutex;
std::atomic_size_t remaining{0};
std::condition_variable cv;
} state;
auto task = [f, &state, begin, end, chunk_size]
(size_t task_id) {
int64_t local_start = static_cast<int64_t>(begin + task_id * chunk_size);
if (local_start < end) {
int64_t local_end = std::min(end, static_cast<int64_t>(chunk_size + local_start));
try {
ParallelRegionGuard guard(static_cast<int>(task_id));
f(local_start, local_end);
} catch (...) {
if (!state.err_flag.test_and_set()) {
state.eptr = std::current_exception();
}
}
}
{
std::unique_lock<std::mutex> lk(state.mutex);
if (--state.remaining == 0) {
state.cv.notify_one();
}
}
};
state.remaining = num_tasks;
_run_with_pool(std::move(task), num_tasks);
// Wait for all tasks to finish.
{
std::unique_lock<std::mutex> lk(state.mutex);
if (state.remaining != 0) {
state.cv.wait(lk);
}
}
if (state.eptr) {
std::rethrow_exception(state.eptr);
}
}
} // namespace internal
// Run lambda function `fn` over `task_id` in [0, `range`) with threadpool.
// `fn` will be called with params: task_id.
static void _run_with_pool(const std::function<void(size_t)>& fn, size_t range) {
#ifndef C10_MOBILE
for (const auto i : c10::irange(1, range)) {
_get_intraop_pool().run([fn, i]() { fn(i); });
}
// Run the first task on the current thread directly.
fn(0);
#else
caffe2::PThreadPool* const pool = caffe2::pthreadpool();
TORCH_INTERNAL_ASSERT(pool, "Invalid thread pool!");
pool->run(
// PThreadPool::run() is blocking. A std::function [const] reference to
// this lambda cannot go out of scope before PThreadPool::run() returns.
[&fn](const size_t task_id) {
fn(task_id);
}, range);
#endif // C10_MOBILE
}