DnCC Assignment 1: Parallel Matrix Multiplication

https://github.com/HaibinLai/Distributed-and-Cloud-Computing.git

【分布与云计算 - DnCC 复习】 https://www.bilibili.com/video/BV1eovaBTEW9/?share_source=copy_web&vd_source=72eac555730ba7e7a64f9fa1d7f2b2d4

Setup

Compile

We can use OpenMPI or Intel MPI to compile and run the code.

To use OpenMPI, we can install it from official website:
https://www.open-mpi.org/software/ompi/v5.0/

For ubuntu user it can install using apt.

sudo apt install openmpi-bin libopenmpi-dev

To use Intel MPI, you can use the following command after installing from Intel MPI https://www.intel.com/content/www/us/en/developer/tools/oneapi/base-toolkit-download.html

# source /path/to/intel/setvars.sh # if use 
mpicc mpi_matrix_base.c -o mpi_matmul

Run the code

mpirun -np 4 ./mpi_matmul

Program Design

The process of the program is shown as following:

1. Init matrix data.
2. Do data distribution to every workers using MPI_Scatterv and MPI_Bcast.
3. For each workers and root, receive and compute the data
4. Use MPI_Gatherv to collect the result
   

We spilt matrix A and do computation with B:

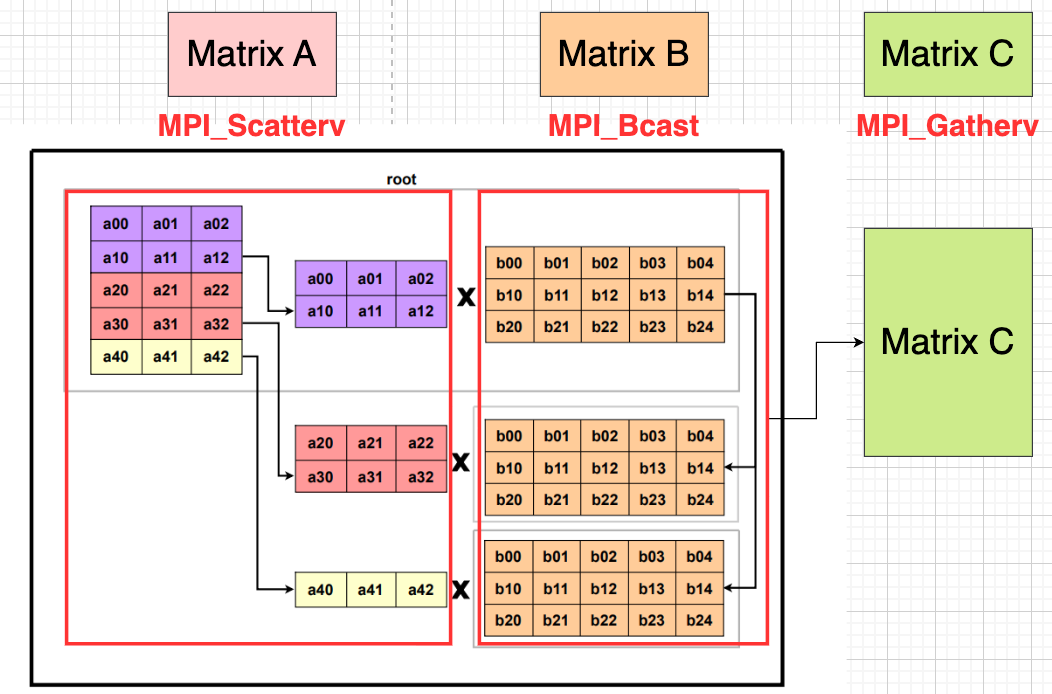
And it provides the correct result since we can do it mathematically:
$$AB= \begin{bmatrix} A^{(1)}\ A^{(2)}\ \vdots\ A^{(P)} \end{bmatrix} B = \begin{bmatrix} A^{(1)}B\ A^{(2)}B\ \vdots\ A^{(P)}B \end{bmatrix}=\;\begin{bmatrix} C^{(1)}\ C^{(2)}\ \vdots\ C^{(P)} \end{bmatrix}=C\;$$

Init

Warning: if the size is greater than 512, it will cause fault. To solve this, a optimal solution is to assign them on heap by using malloc.

int rank, mpiSize;
double a[MAT_SIZE][MAT_SIZE],      /* matrix A to be multiplied */
         b[MAT_SIZE][MAT_SIZE],       /* matrix B to be multiplied */
         c[MAT_SIZE][MAT_SIZE],       /* result matrix C */
         bfRes[MAT_SIZE][MAT_SIZE];   /* brute force result bfRes */

/* You need to intialize MPI here */
MPI_Init(&argc, &argv);
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
MPI_Comm_size(MPI_COMM_WORLD, &mpiSize);

Communication

We use MPI_Scatterv to separate matrix A, and use MPI_Bcast to send matrix B to each process.

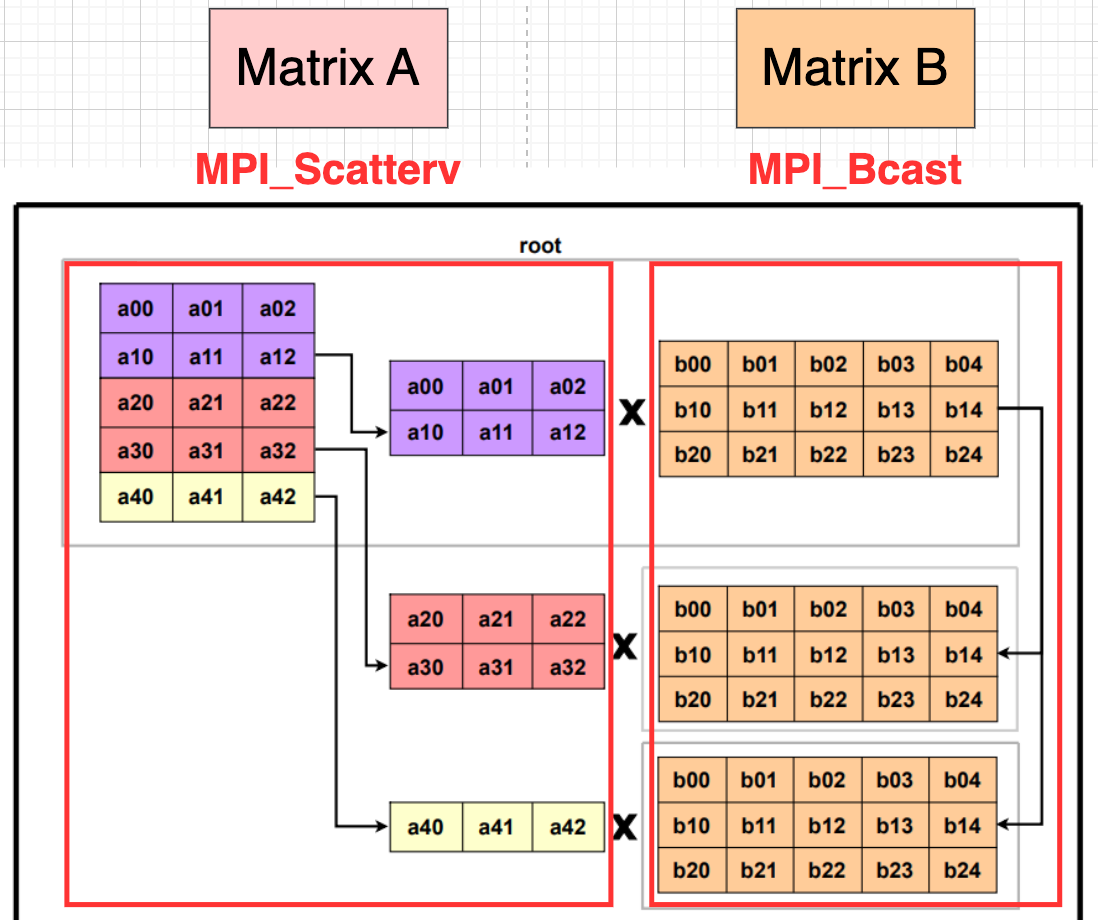
The Broadcast code is shown as following.

1. Broadcast matrix B.
2. Calculate number of elements and offsets of A for each processes.
3. Each process inits buffer A_local and C_local for receiving data and computation.
4. Broadcast matrix A.

/* Send matrix data to the worker tasks */
MPI_Bcast(&b[0][0], MAT_SIZE*MAT_SIZE, MPI_DOUBLE, 0, MPI_COMM_WORLD);

// split A by row
int rows_per_proc = MAT_SIZE / mpiSize;
int rem = MAT_SIZE % mpiSize;
int offset = 0;
for (int p = 0; p < mpiSize; p++) {
    int rows = rows_per_proc + (p < rem ? 1 : 0);
    sendcounts[p] = rows * MAT_SIZE;     // number of elements
    displs[p]     = offset * MAT_SIZE;   // displacement (in elements)
    offset += rows;
}
myrows = sendcounts[rank] / MAT_SIZE;

// each process's local buffer
double *A_local = malloc((size_t)myrows * MAT_SIZE * sizeof(double));
double *C_local = calloc((size_t)myrows * MAT_SIZE, sizeof(double));

// distribute rows of A
MPI_Scatterv(&a[0][0], sendcounts, displs, MPI_DOUBLE,
    A_local, myrows*MAT_SIZE, MPI_DOUBLE,
    0, MPI_COMM_WORLD);

Why we use MPI_Scatterv:
MPI_Scatter distributes equal-sized chunks of data from the root to all processes, so every process receives the same number of elements.
MPI_Scatterv is more flexible: it allows variable-sized chunks, using sendcounts and displs to specify how much data each process gets and where it starts in the buffer.

Since we may not divide all the data equally (like for N=500, process_num=8), there must have a process take extra computation.

Local Computation

Same as single thread computation.

/* Compute its own piece */
for (int i = 0; i < myrows; i++) {
    for (int k = 0; k < MAT_SIZE; k++) {
        double a_k = A_local[i*MAT_SIZE + k];
        for (int j = 0; j < MAT_SIZE; j++) {
            C_local[i*MAT_SIZE + j] += a_k * b[k][j];
        }
    }
}

Gather the result

We use MPI_Gatherv to collect result to matrix c. The reason for using MPI_Gatherv rather than MPI_Gather is the same as MPI_Scatterv.

MPI_Gatherv(C_local, myrows*MAT_SIZE, MPI_DOUBLE,
    &c[0][0], sendcounts, displs, MPI_DOUBLE,
    0, MPI_COMM_WORLD);

Experiments

Testbed

We conducted the evaluation on a machine with an Intel(R) Xeon(R) Gold 5320 CPU (52 physical cores / 104 threads), 128 GB of memory, running Ubuntu 22.04 with OpenMPI 4.0.3 version.

Strong Scaling Analysis

Here we do the experiments to see the relationships between the number of processes in MPI and the running time.

We run it locally with 1, 2, 4, 8, 16 and 32 processes with $N=500$ matrix size.

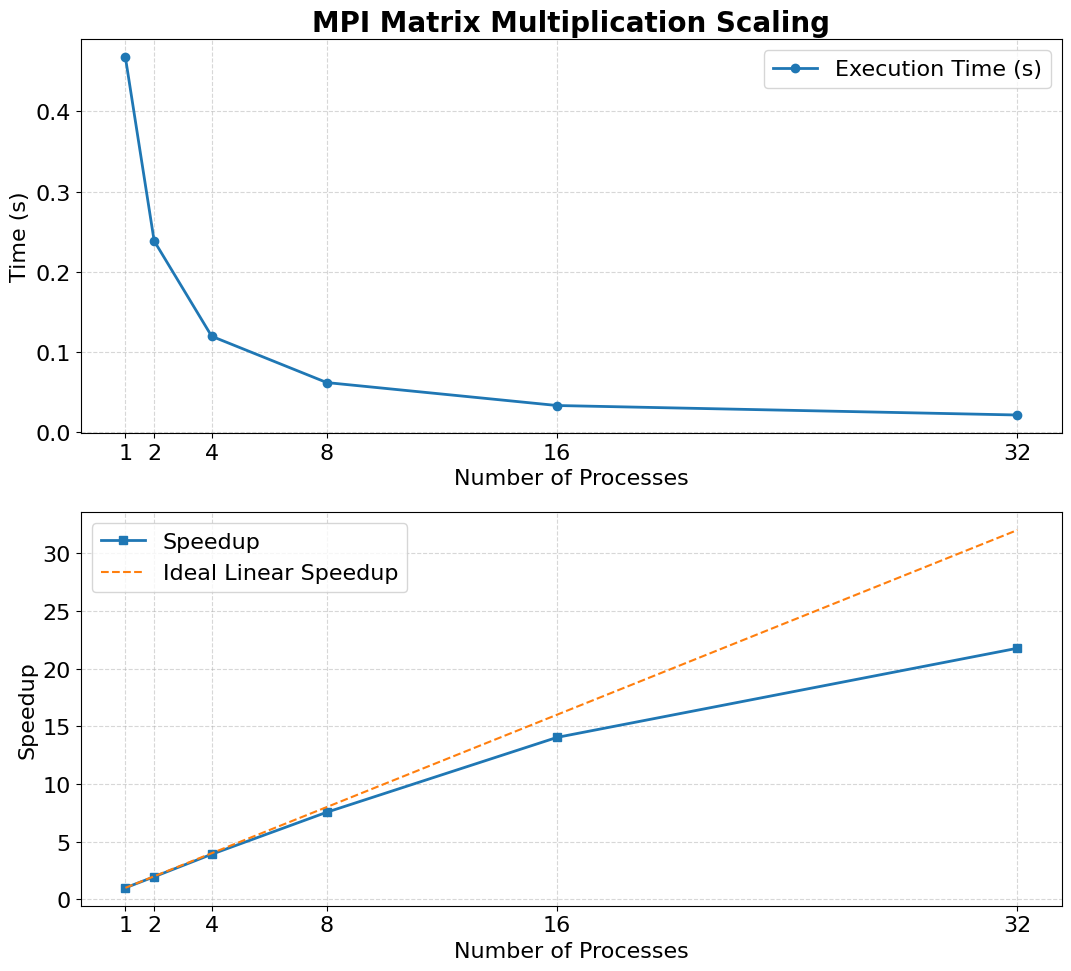
We can see that as the number of processes rises, the speedup ratio gets lower than the ideal linear speedup.

We use Amdahl's Law to analysis.

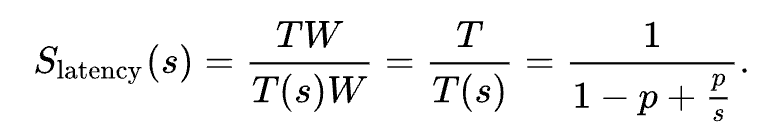
The speedup of a parallel program is limited by the fraction of the code that remains sequential. Even if most of the computation can be parallelized, the serial portion and communication overhead prevent achieving ideal linear scaling. In our case, using 32 processes cannot give 32× acceleration because synchronization, data distribution, and non-parallelizable parts dominate at higher process counts. Thus, the law predicts diminishing returns as the number of processes increases.

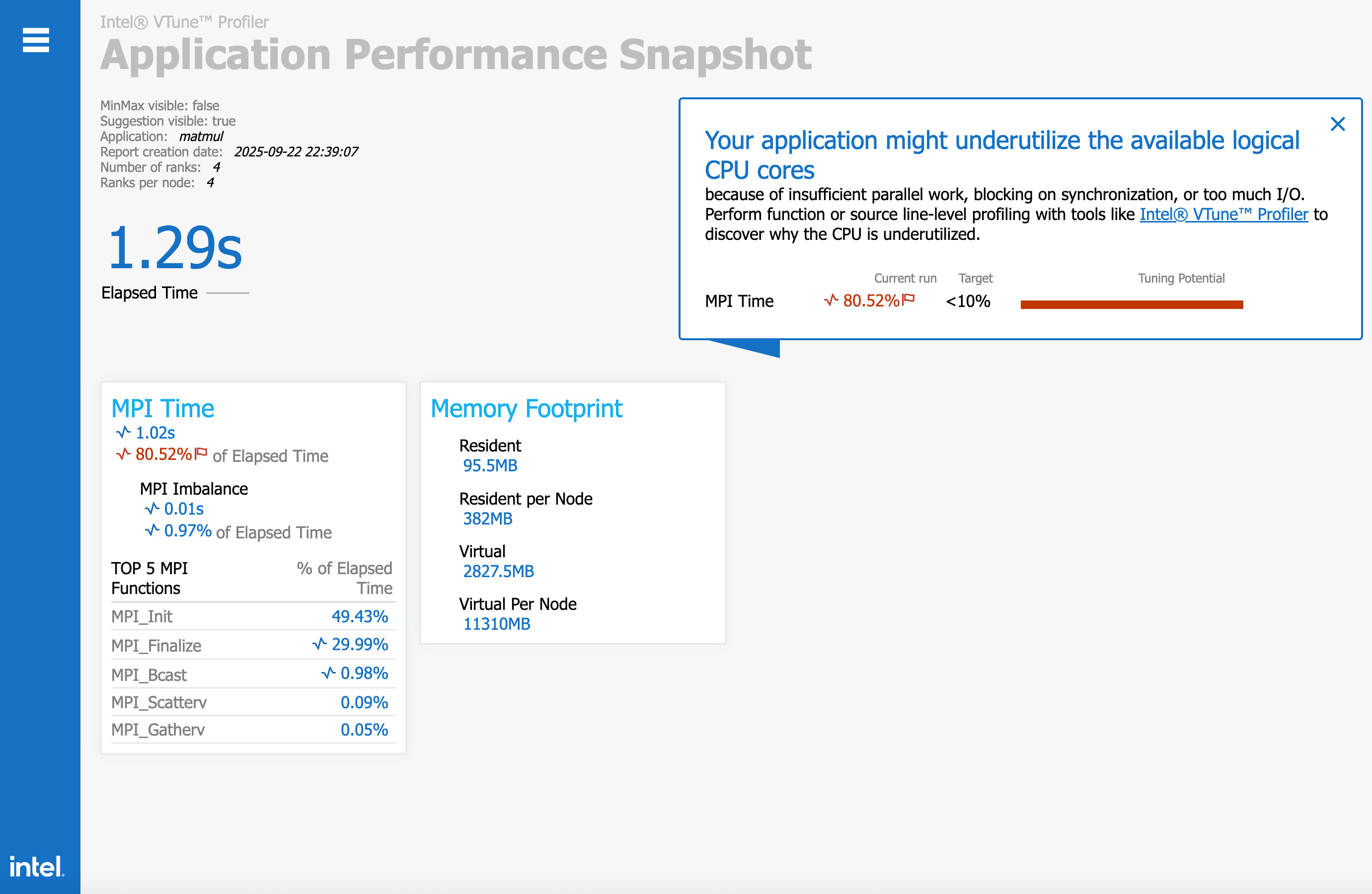
Using intel ipm profiler to profile MPI time

We use following variable to initiate intel mpi profiler:

source /path/to/intel/setvars.sh
export I_MPI_STATS=5
mpirun -np 4 ./matmul # run the mpi program
aps --report /path/to/report

We can see that the whole program use 1.29s (from main function, matrix init to return 0), among MPI_Bcast, MPI_Scatterv, MPI_Gatherv, we can see that MPI_Bcast rank 1st for this 3 functions (This is obvious, since we use MPI_Bcast to separate matrix B).

Time Comparison for different Matrix Size

Here we do the experiments to test the time of brute-force algorithm and MPI implementation as the matrix size N changes.

We test $N = {10, 50, 100, 250, 500}$ with process from 1,2,4,8,16,32.

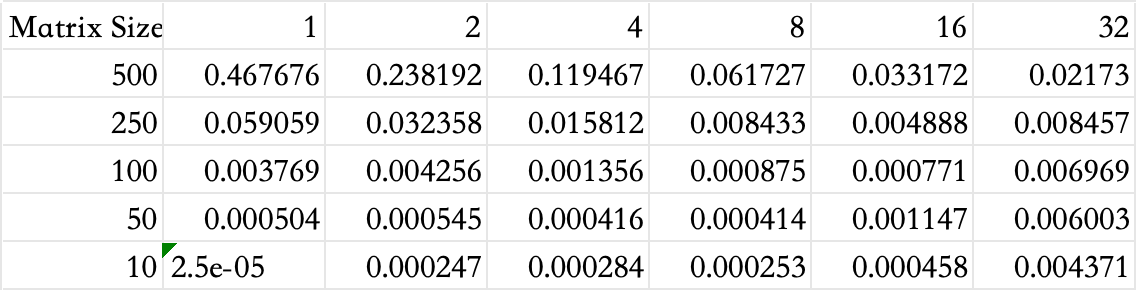
baseline

baseline = {
    10: 0.000004,
    50: 0.000580,
    100: 0.004633,
    250: 0.057622,
    500: 0.455162,
}

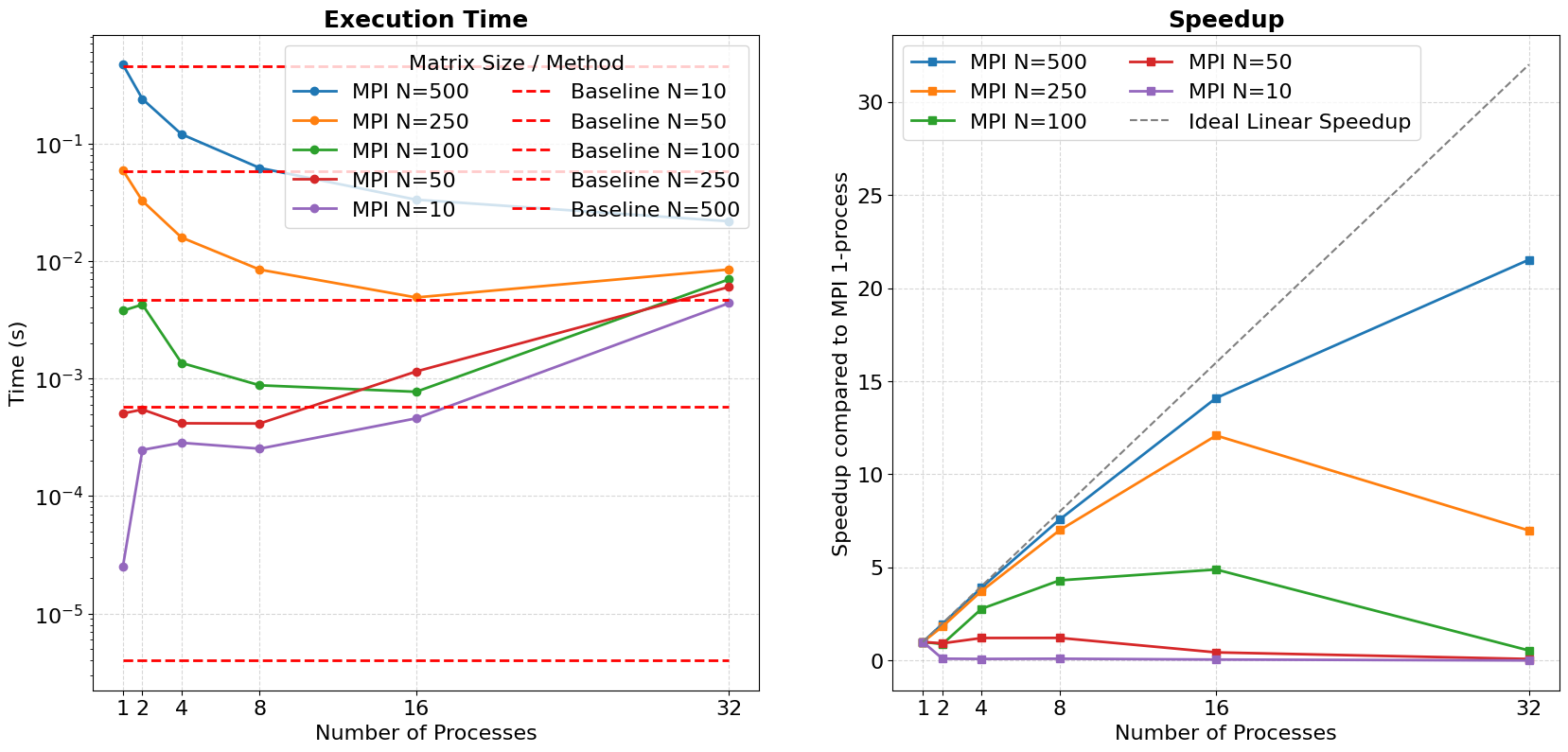
We can see that for single thread, the MPI program needs more time than baseline brute force matmul. While as the processes number goes up, for large matrix size like N=250, N=500, we gain some performance. But since the synchronization overhead rises up as the number of process rise up, we see performance slow down. (like N=250, p=32, we get less speedup)

As for single thread MPI program, they still have some overhead on MPI and data movement. We can see this from assembly:

mpigcc -g -S -fverbose-asm -masm=intel mpi_matrix_base.c -o run_asm

For example, we can see the asm code for MPI_Scatterv, here the compiler will let the program to save its register data and call MPI_Scatterv@PLT from runtime library, which cause some overhead.

# mpi_matrix_base.c:83:       MPI_Scatterv(&a[0][0], sendcounts, displs, MPI_DOUBLE,
    .loc 1 83 7
    mov eax, DWORD PTR -8000124[rbp]    # tmp243, myrows
    imul    edi, eax, 500   # _34, tmp243,
    mov rcx, QWORD PTR -8000048[rbp]    # tmp244, A_local
    mov rdx, QWORD PTR -8000088[rbp]    # tmp245, displs
    mov rsi, QWORD PTR -8000096[rbp]    # tmp246, sendcounts
    lea rax, -8000016[rbp]  # tmp247,
    sub rsp, 8  #,
    push    1140850688  #
    push    0   #
    push    1275070475  #
    mov r9d, edi    #, _34
    mov r8, rcx #, tmp244
    mov ecx, 1275070475 #,
    mov rdi, rax    #, tmp247
    call    MPI_Scatterv@PLT    #
    add rsp, 32 #,

Docker execution result

My docker file struct:

.
├─ Dockerfile
├─ docker-compose.yml
├─ entrypoint.sh
├─ work/                 # /workspace
│  ├─ matmul             
│  ├─ hosts              
│  └─ ssh/               

download ubuntu 22.04 image from https://cdimage.ubuntu.com/ubuntu-base/releases/22.04/release/

# ubuntu-base-22.04.5-base-amd64.tar.gz:
wget https://cdimage.ubuntu.com/ubuntu-base/releases/22.04/release/ubuntu-base-22.04-base-amd64.tar.gz

import as docker image

cat ubuntu-base-22.04-base-amd64.tar.gz | sudo docker import - ubuntu:22.04

build my container:

ssh-keygen -t rsa -b 4096 -N "" -f work/ssh/id_rsa
docker compose up -d --build

From this ubuntu linux image, we further build a docker image with openssh and openmpi.

FROM ubuntu:22.04

# OpenMPI & OpenSSH
ENV DEBIAN_FRONTEND=noninteractive
RUN apt-get update && \
    apt-get install -y --no-install-recommends \
      build-essential openmpi-bin libopenmpi-dev \
      openssh-server openssh-client ca-certificates sudo && \
    rm -rf /var/lib/apt/lists/*

# mpi User
RUN useradd -ms /bin/bash mpi && echo "mpi ALL=(ALL) NOPASSWD:ALL" >> /etc/sudoers

# SSH 
RUN mkdir -p /var/run/sshd
RUN sed -ri 's/^#?PasswordAuthentication .*/PasswordAuthentication no/' /etc/ssh/sshd_config && \
    sed -ri 's/^#?PermitRootLogin .*/PermitRootLogin no/' /etc/ssh/sshd_config && \
    echo "PubkeyAuthentication yes" >> /etc/ssh/sshd_config

WORKDIR /workspace
COPY entrypoint.sh /entrypoint.sh
RUN chmod +x /entrypoint.sh && chown -R mpi:mpi /workspace

# USER mpi
ENTRYPOINT ["bash", "/entrypoint.sh"]
# ENTRYPOINT ["/entrypoint.sh"]

In docker-compose.yml file, we let ./work map to /workspace inside docker nodes.

version: "3.8"

services:
  node1:
    build: .
    container_name: node1
    hostname: node1
    networks: [cluster]
    volumes:
      - ./work:/workspace
    ports:
      - "2201:22"   

  node2:
    build: .
    container_name: node2
    hostname: node2
    networks: [cluster]
    volumes:
      - ./work:/workspace
    ports:
      - "2202:22"

  node3:
    build: .
    container_name: node3
    hostname: node3
    networks: [cluster]
    volumes:
      - ./work:/workspace
    ports:
      - "2203:22"

networks:
  cluster:
    driver: bridge

In entrypoint.sh, we let each nodes connect to each other with ssh.

#!/usr/bin/env bash
set -euo pipefail

user=mpi
home=/home/$user

if [ "$(id -u)" != "0" ]; then
  echo "This entrypoint must run as root."
  exit 1
fi

mkdir -p /etc/ssh
ssh-keygen -A

mkdir -p "$home/.ssh" /var/run/sshd /workspace/ssh
chmod 700 "$home/.ssh"

if [ ! -f /workspace/ssh/id_rsa ]; then
  ssh-keygen -t rsa -b 4096 -N "" -f /workspace/ssh/id_rsa
fi
cp /workspace/ssh/id_rsa{,.pub} "$home/.ssh/"
cat /workspace/ssh/id_rsa.pub >> "$home/.ssh/authorized_keys"

cat > "$home/.ssh/config" <<EOF
Host *
  StrictHostKeyChecking no
  UserKnownHostsFile /dev/null
  LogLevel ERROR
EOF

chown -R $user:$user "$home/.ssh"
chmod 600 "$home/.ssh"/*

# 3) sshd
/usr/sbin/sshd

# 4) mpi user
exec su - $user -c "cd /workspace && tail -f /dev/null"

We enter node1 as user mpi

sudo docker exec -it -u mpi node1 /bin/bash

And we compile the code and run it:

sudo mpicc mpi_matrix_base.c  -o matmul
mpirun --oversubscribe -np 8   --hostfile /workspace/hosts   --mca plm_rsh_agen
t "ssh -l mpi"   -mca btl_tcp_if_include eth0   ./matmul 500

Then we can see Result is correct.:

Cheers!

---

Some possible Optimizations on Matmul

Better Matmul

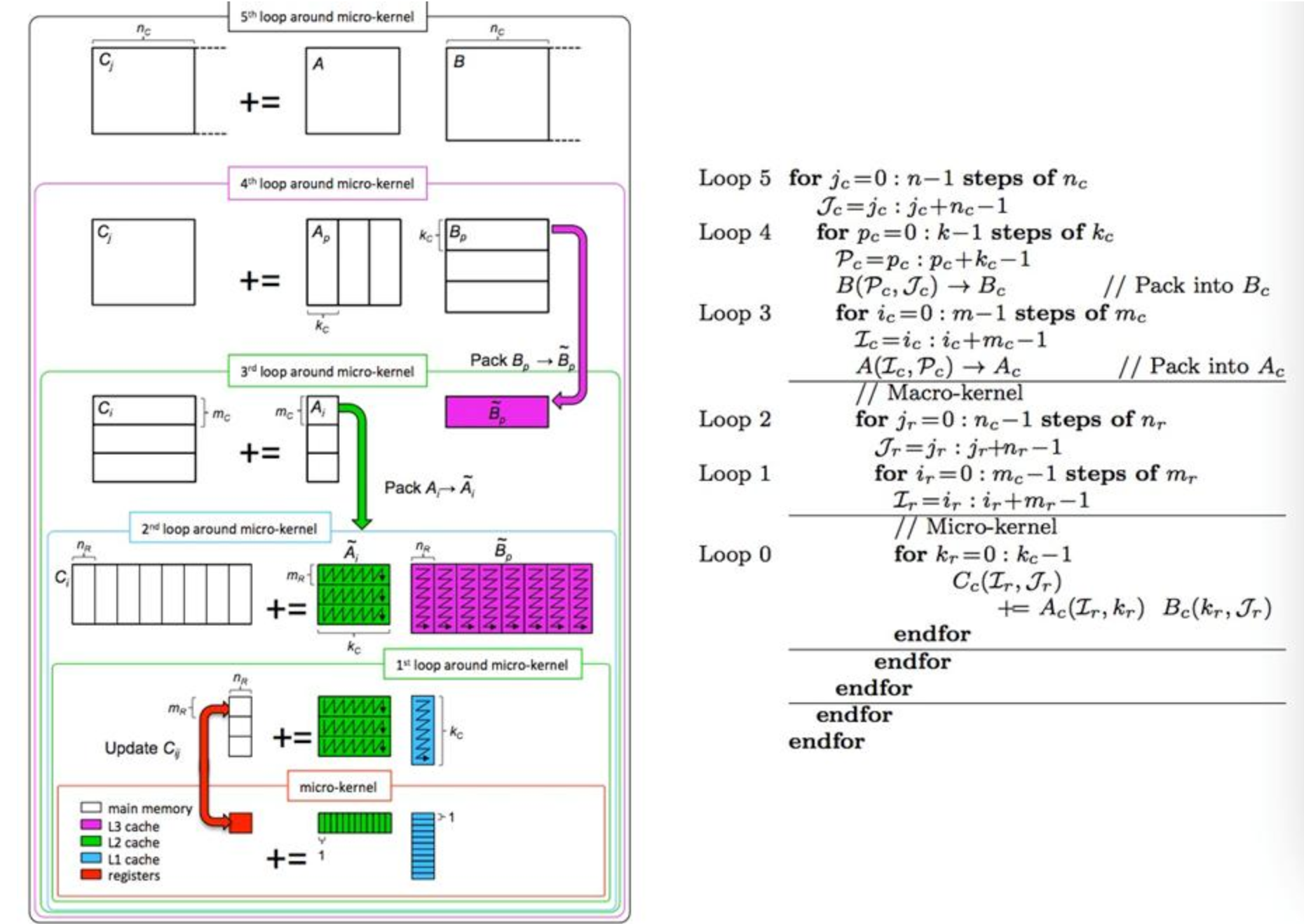
We can optimize matmul using:

1. matrix tilling
2. SIMD instructions like AVX512, or matmul instructions like Intel AMX
3. Loop unrolling
4. MPI+OpenMP hybrid running

I implemented 1,2,3 and OpenMP for a matmul program in my CPP Programming Project, feel free to see my report (unfortunately it's still in Chinese, I plan to translate them in English in the future):
https://github.com/HaibinLai/CS205-CPP-Programing-Project/tree/main/Project3

If you are interested in my optimization in Matmul, feel free to visit some of my projects blogs:

本科生能做并行计算hpc吗？ - 笑到猝死的家伙的回答 - 知乎
https://www.zhihu.com/question/657927103/answer/1896769963135578670

Compute-Communication Overlapping

In the previous program, we first distribute all the data to each of the processes, then we do the computation. But here a performance issue rises: when the memory is busy transferring data (if the processes do transfer process using DMA or NIC), the CPU Computing part is idle.

So one of the idea is to do overlapping. After getting all the data, we may use async MPI api like MPI_Isend with a technique call double buffer as the following figure shows:

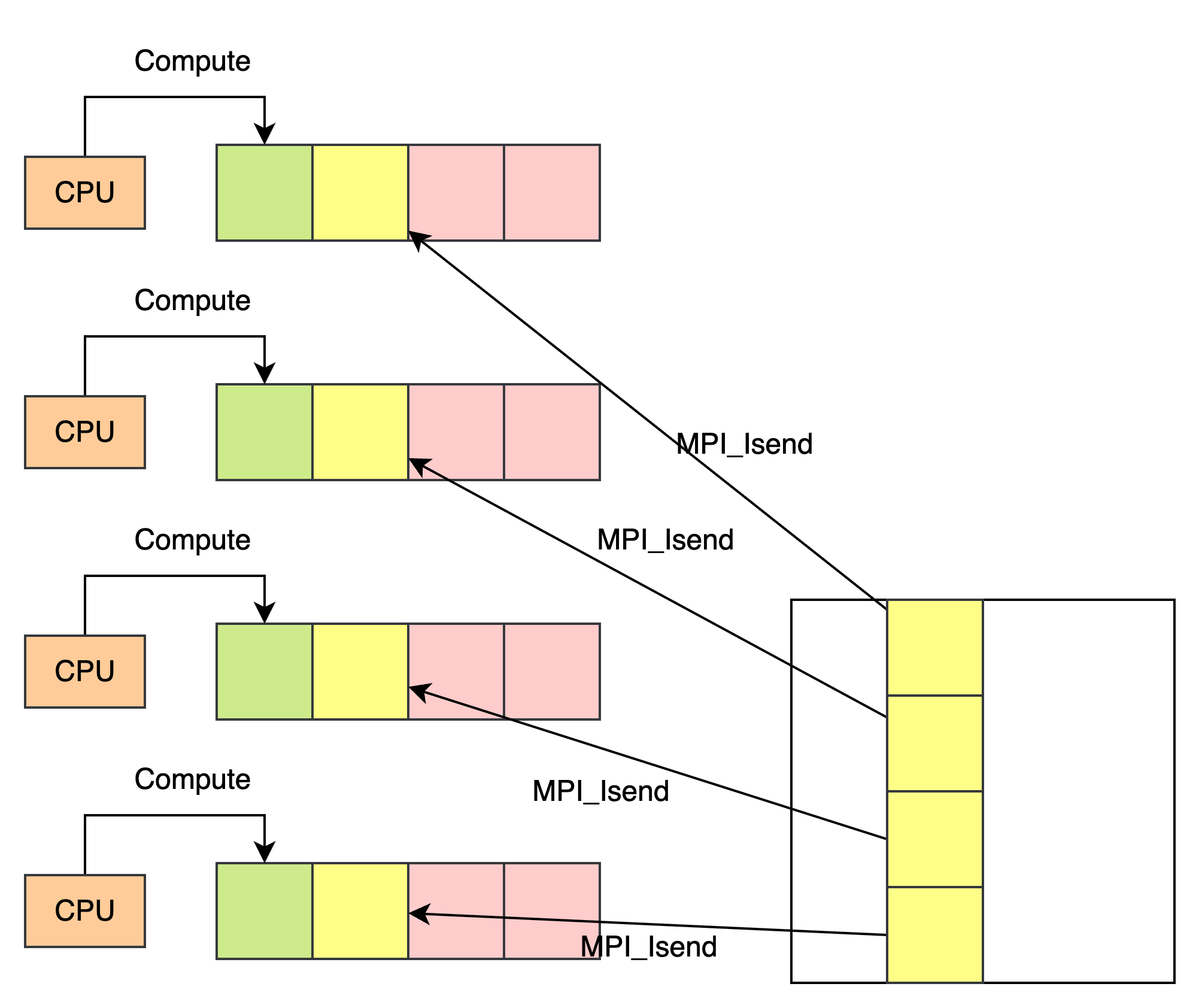
So when the CPU workers are calculating the part, we can let MPI to prefetch the next data blocks from root process.

int cur = 0, next = 1;

compute_and_communicate_first_block(...);

for (int t = 1; t < T; ++t) {
  // init next blocks and calculate val "cur" and "next"
  calc_count_displs_for_block(t, ...);
  MPI_Iscatterv(&A[0][0], countsA_blk, displsA_blk, MPI_DOUBLE,
                Ablk[next], rows_t*N_local, MPI_DOUBLE, 0, MPI_COMM_WORLD);

  // Compute (Overlap with Iscatterv)
  compute_block(Ablk[cur], B, Cblk[cur], rows_cur, N);

  // wait until Ablk[next] is ready
  MPI_Wait(&rq_scatter, MPI_STATUS_IGNORE);

  // collect data
  MPI_Igatherv(Cblk[cur], rows_cur*N, MPI_DOUBLE,
               &C[0][0], countsC_blk_cur, displsC_blk_cur, MPI_DOUBLE, 0, MPI_COMM_WORLD);

  // swap buffer
  int tmp = cur; cur = next; next = tmp;

  // test if Igatherv complete
  MPI_Wait(&rq_gather, MPI_STATUS_IGNORE);
}

Runtime graph:

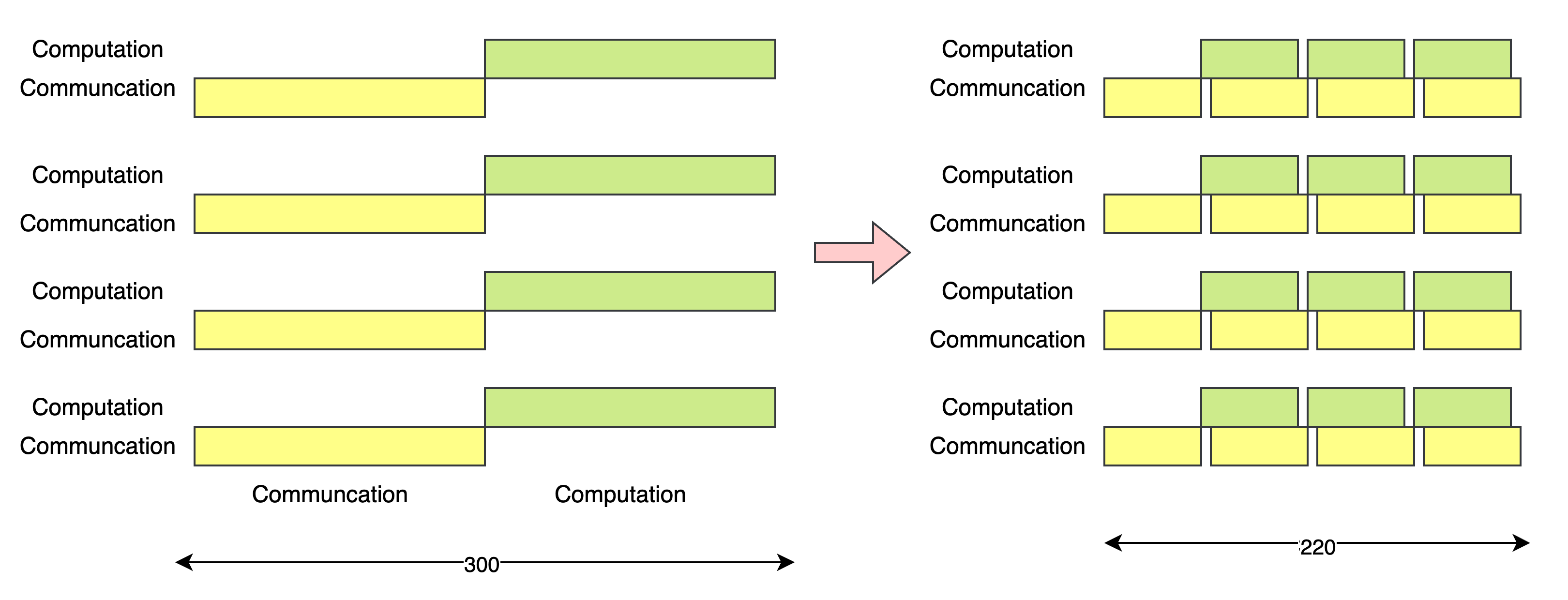
I have done this on GPU Matmul before, if you are interested, feel free to see my Optimization for SGEMM in GPU
https://github.com/HaibinLai/SUSTech-HGEMM

MPI

I learn MPI programming on my second year of undergraduate, when I was participating in Supercomputing Challenge Competition. Last year on a competition called APAC HPC-AI, my job is to optimize an HPC software call Hoomd-blue. Hoomd-blue simulates chemical molecular on distributed systems using MPI primitives like MPI_Allreduce.

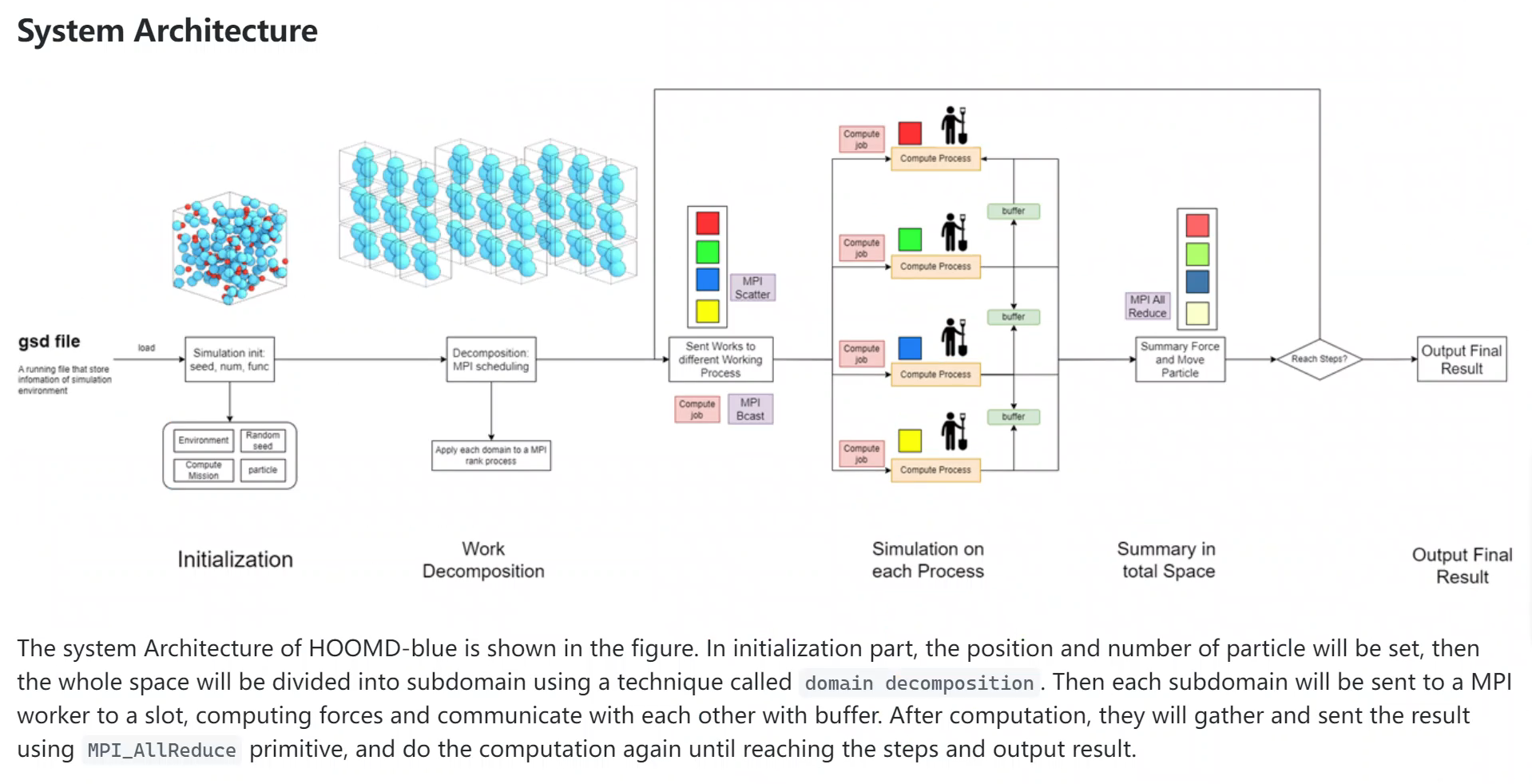
OpenMPI uses different algorithm to do MPI_AllReduce, like butterfly algorithm, reduce+broadcast algorithm, Ring algorithm etc.

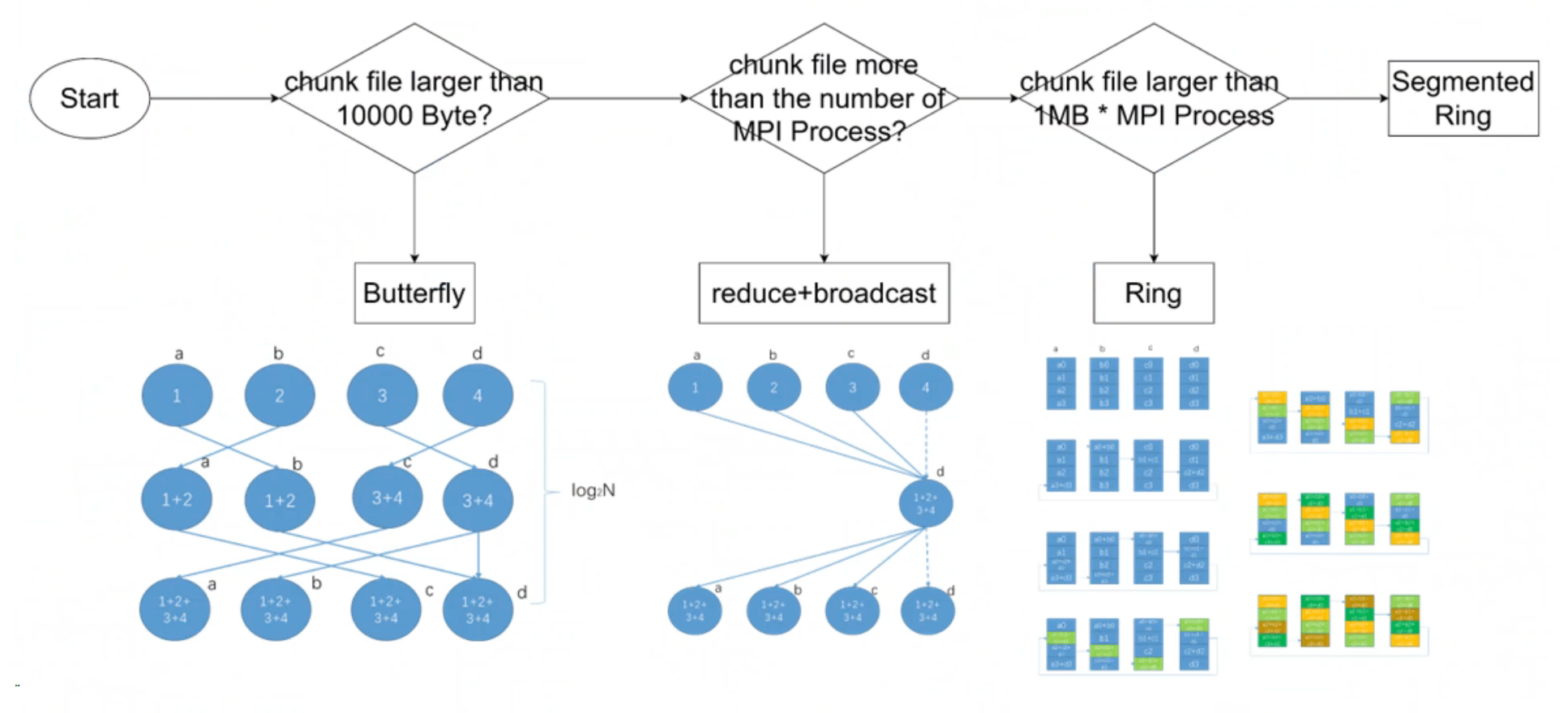
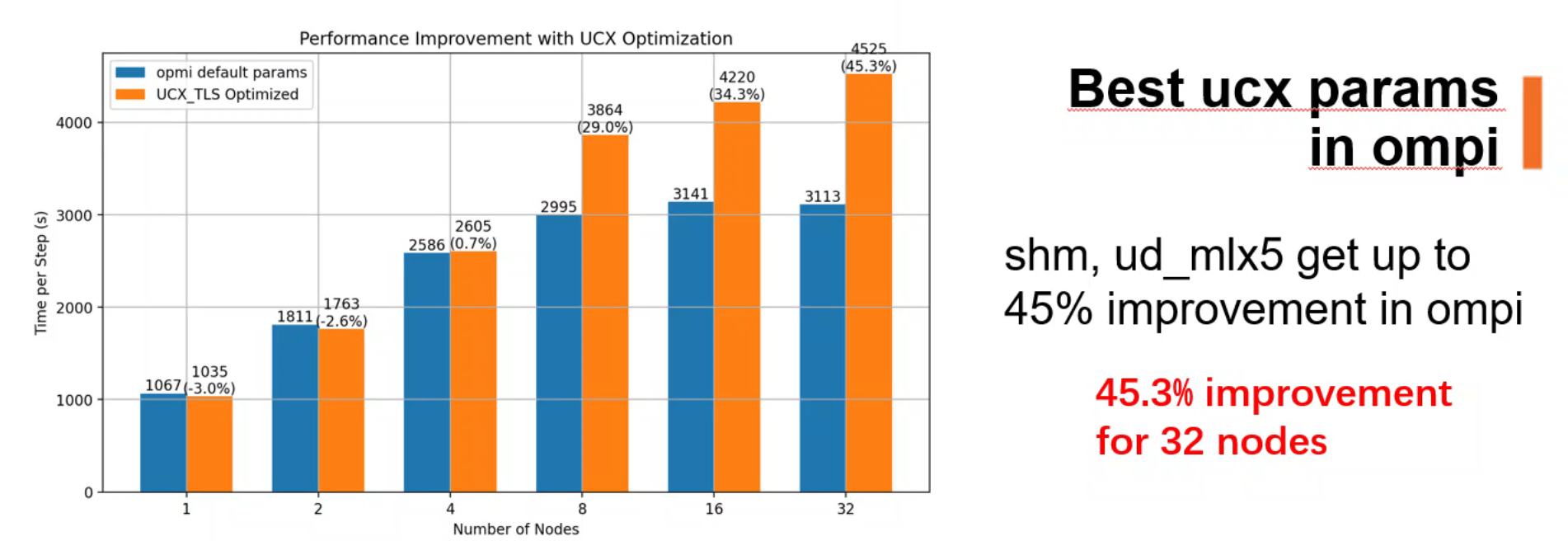
I optimize MPI with different parameters and how the program utilizes MPI.

---

Before the 1990s, parallel computers used many different message-passing libraries (such as PVM, NX, and Express), each with its own interface and limitations. To address the lack of a unified standard, the MPI Forum was established in 1992, bringing together researchers from academia and industry. In 1994, the first MPI standard was released, which quickly became the de-facto communication standard for high-performance computing.

Professor Jack Dongarra played a key role in this history. He emphasized that MPI must serve as a solid communication layer for scientific computing libraries, and he actively helped bridge the gap between academic research and industrial implementations, ensuring MPI’s rapid adoption.

I was fortunate to meet Professor Dongarra in person and take a photo with him. For me, this moment felt like connecting directly with the history of parallel computing.