CPP Project2 Matrix Multiplication
- CPP
- 2024-09-06
- 2688 Views
- 0 Comments
CS205·C/C++ Programming
Project2 Report: Matrix Multiplication
PDF 版本:Project2赖海斌
Github: https://github.com/HaibinLai/CS205-CPP-Programing-Project
摘要
同样是矩阵乘法,Java和C谁更快?在做Project之前,我会凭着经验和对于老师的信任大声告诉你答案。但是在做了本次Project后,我只能笑着不能告诉你答案。我一共做了四个实验,第一个实验发现Java在执行时会自动判定float精度,而C不会。我进而认为Java程序的JVM对Java影响很大,进而去探索了JIT对Java影响和被翻译成汇编的Java和C以及C -O3的x86汇编代码,发现JIT的C1C2编译器效果不明显,而-O3编译优化将原本在栈上的ijk变量优化到放入寄存器中,尝试减少程序的汇编指令数以及减少花费高昂的内存读取指令的次数,因而降低了运行时间。随后实验3我进行了速度测试,发现在不同平台上Java和C的表现有所差异,在软硬件环境和编译器不同的情况下Java还真不一定比C慢。同时我也探测到Java多线程和C OpenMP在通信上的瓶颈,多线程并不一定比单线程强。实验4我探索了Java和C不同的启动方式以及Linux和Windows操作系统唤起程序的方式。同时我还用Intel TopDown性能分析法分析了Java和C程序的运行瓶颈,分析了程序CPI变化的原因。
在硬件、软件上的众多区别,使得我们的实验就像进入到《黑客帝国》里的Matrix,复杂的环境下一切皆有可能发生。但是通过这次的理论和实验,作为Mr.Anderson,我们离Neo更近了一步。
关键词:汇编分析;速度测试;微处理探索;Top Down性能分析;
Part 1: 实验需求分析
矩阵相乘是一个重要的计算机基础运算,这次Project要求我们计算矩阵相乘,并对Java和C语言的实现进行比较。我想老师希望我们从中学习的,是C为什么性能高(Why)。同时我也好奇,C如何提高性能(How),单纯的上OpenMP或者CUDA效果有多大?
所以,本次实验,我想建立这么几个观测目标:
1.时间损耗:这里边可能存在的问题是,1.用Profiler统一测量时间好,还是在各自语言内写函数记录?2.参考数据库Project,JIT是否会影响时间?3.单核跟多核的性能是否会影响时间?
2.性能跟踪:这里我们可以引入并行计算里的理论来测量。可能的问题是,1.C和Java程序分别是怎么跑起来的?2.虚拟机与内部GC怎么影响我们的程序?3.不同的处理器是否会使性能发生改变?
3.运行加速:1.Java的多线程能够提升几倍?OpenMP呢?为什么他们的效率不一样?GPU提升的效率是怎么样的?2.使用-O3,-O2真的会使我们的程序加速吗,为什么?
4.算法升级:矩阵乘法真的只能在O(n3)实现吗?有没有更快的方法?他们应用的多吗?这部分只是针对这次Project的程序,也是给后面在优化上让我有更多的了解。
Part 2: 实验设备与仪器
本节介绍我们的实验“试管”和“试纸”——硬件设备和观测软件。我们本次使用两个试管:一台Linux浪潮服务器和我的Windows华为笔记本电脑。
2.1 实验仪器1
本次实验的仪器1——“试管1号”服务器,我们使用AMD Processor作为我们的CPU。感谢肖翊成和邱俊杰同学在装机和配置系统上的帮助。
| CPU Architecture | x86_64 |
|---|---|
| Model name | AMD EPYC 7773X 64-Core Processor |
| CPU family | 25 |
| Thread(s) per core | 1 |
| CPU(s) | 128 |
| Core(s) per socket | 64 |
| Memory | 185GiB |
| Cache | 1.5GiB |
| CPU Frequency | 3.5GHz |
表2.1 “试管1号”硬件CPU
2.2 实验仪器2
为了方便运行Java和查看运行程序,我们的实验仪器2——“试管2号”电脑就直接是我的笔记本。试管1号的单核CPU要比试管2号优秀,我们会在后面的效率比较实验(实验3)时完全在试管1号上运行。在实验2和4,我们会比较我们的程序在汇编层级的代码,此时我们将使用Intel Vtune Profiler,因此我们将在试管2号上进行实验。
| CPU Architecture | x86_64 |
|---|---|
| CPU name | 11th Gen Intel(R)Core i7-11370H @ 3.30GHZ |
| CPU family | 6 |
| Thread(s) per core | 2 |
| CPU(s) | 8 |
| Core(s) per socket | 1 |
| Memory | 15.8GiB |
| Cache | 12MiB |
表2.3 “试管2号”硬件CPU
2.3 实验软件版本
本次主要实验软件为Java jdk和C编译器,具体版本如下表。
| 试管1号 | 试管2号 | |
|---|---|---|
| Java jdk | openjdk 17.0.8 2023-07-18 LTS | openjdk 17.0.10 2024-01-16 |
| gcc | gcc.exe (tdm64-1) 10.3.0 | Ubuntu 13.2.0-4ubuntu3 |
| nvcc | - | V12.4.99 |
表2.4 实验软件版本
2.4 测量时间程序
在Java中,我们采用系统的nanoTime来记录时间,之后通过减法输出程序使用时间。而在C中,我们采用<time.h>里的clock()函数,OpenMP中omp_get_wtime()记录当前时间。

2.5 观测软件

1.Intel® VTune™ Profiler
Intel VTune Profiler是一个全平台性能分析工具,可以多角度分析程序性能瓶颈。我们将对我们的C程序分析,观察其在系统内的运行情况。

2.NVIDIA Nsight™ Compute
NVIDIA Nsight™ Compute 是 CUDA® 的交互式分析器。我们将在CUDA C程序上使用它,分析GPU上的C代码到底是怎么执行地,跟我们的CPU有什么区别。
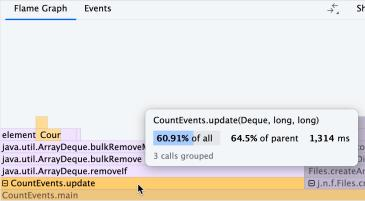
3.IntelliJ Profiler
IDEA的Java性能分析器。考虑到本次我们对Java关心的是JVM底层方面对性能的影响,我们用这个Profiler对Java程序的启动与终止进行分析。
Part 3: 矩阵乘法程序设计
在本次实验里程序结构如下,我们使用简单的Python矩阵生成器利用随机数生成矩阵,随后程序读入并运算,记录结果。我们将查看程序结果和运行时间,并分类讨论:如read和write的时间代表着程序在内存与存储间的I/O速度,对全部使用时间我们会分析程序的启动与终止过程。(程序设计读写及框架由GPT生成)
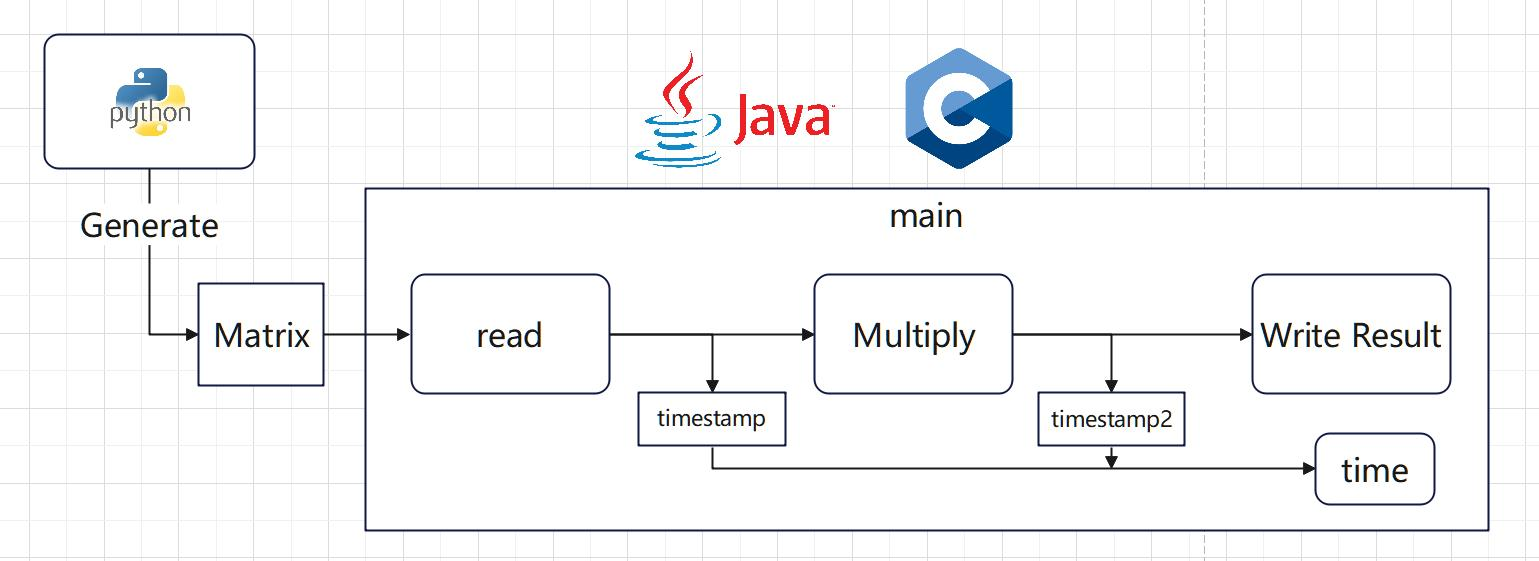
图3.1 Java与C程序架构
下面的函数是Java的读取和写矩阵函数。
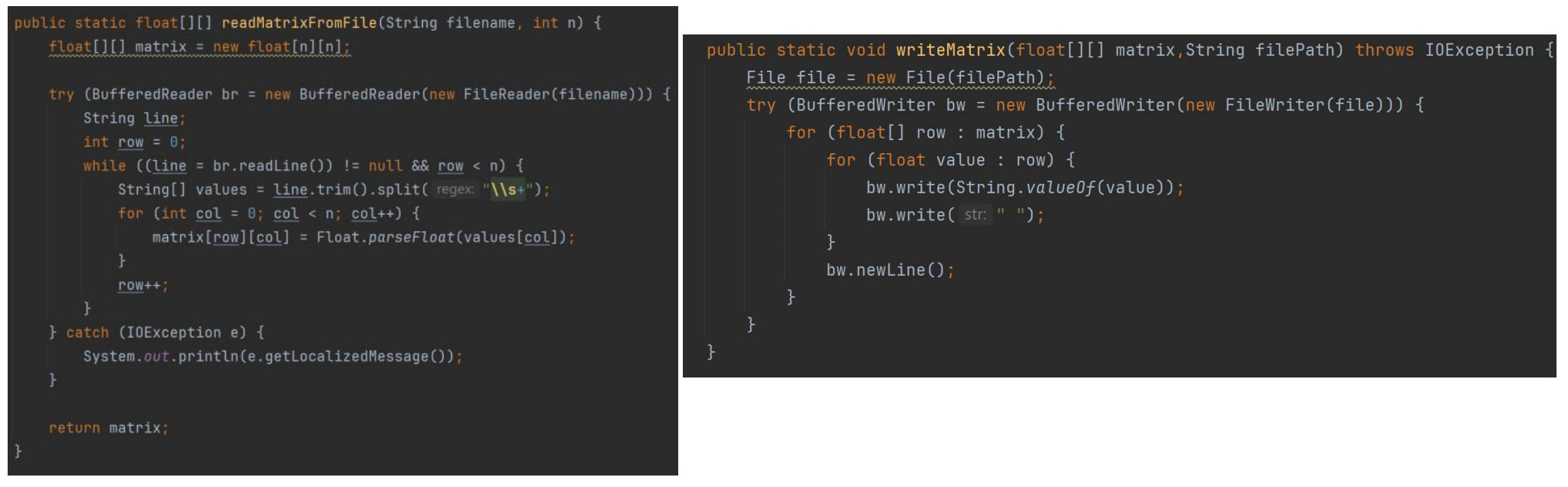
下面是C函数的读取和写函数。
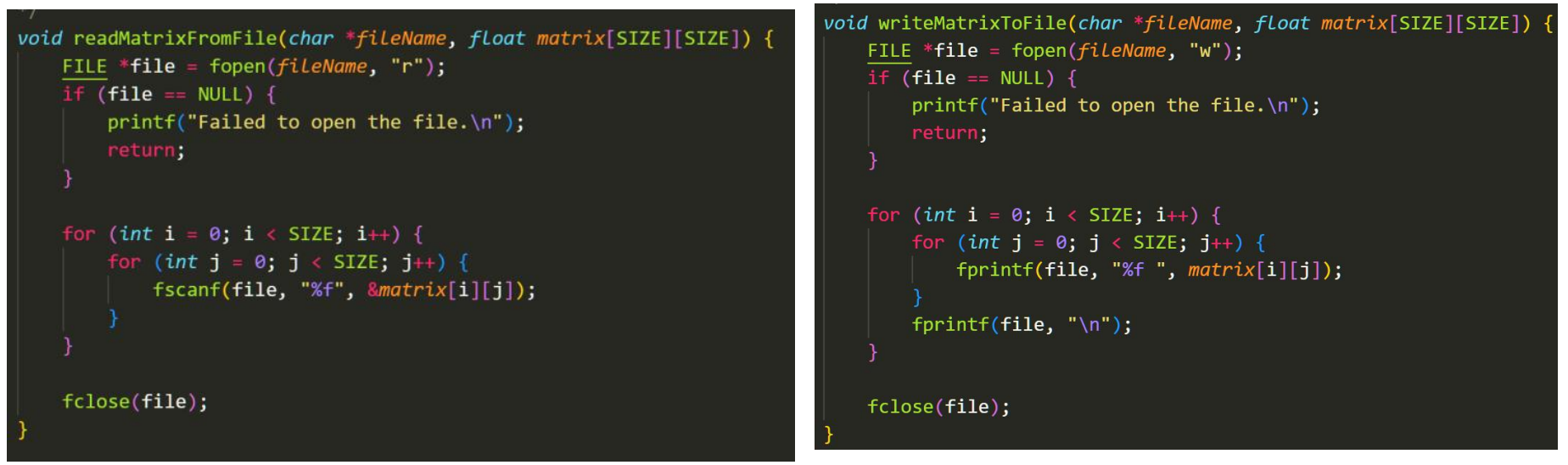
而我们对Java和C各设计了多种乘法程序,以供实验。具体如下图。
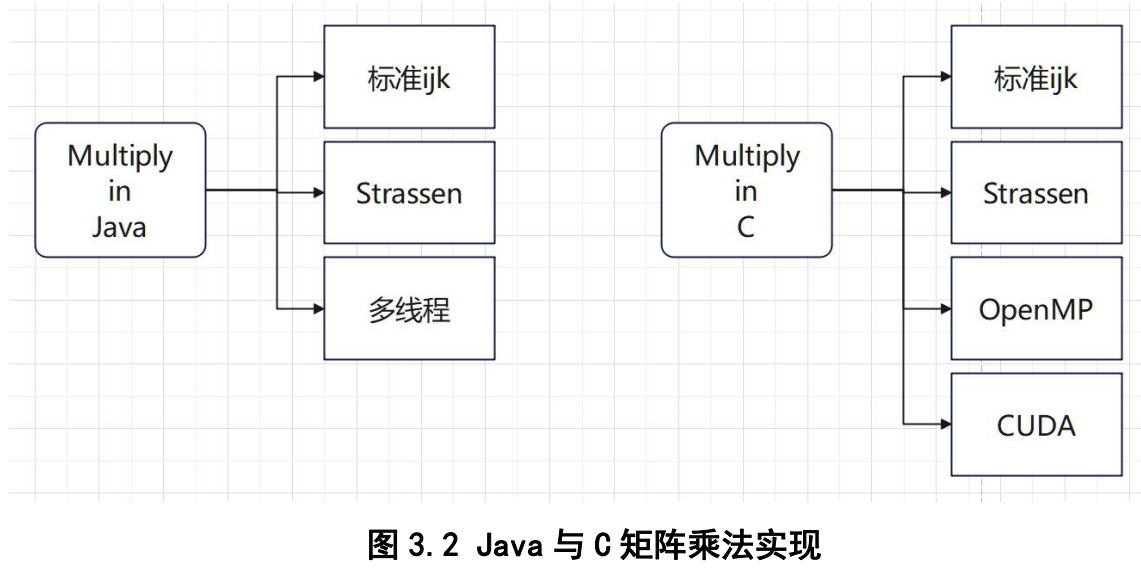
首先是计算复杂度O(n^3)的经典矩阵乘法,它主要有三个for循环,我称其为标准ijk算法。

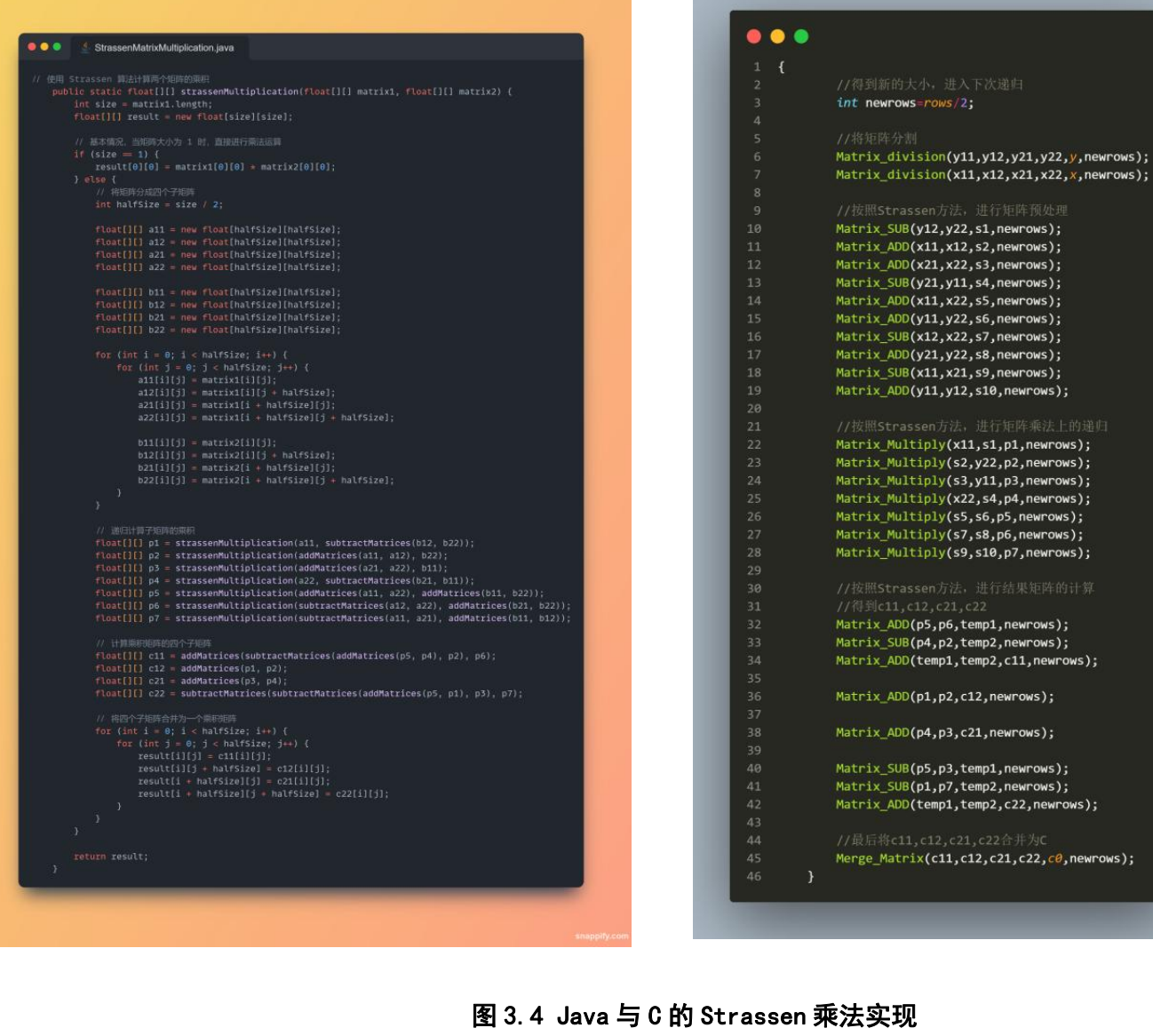
Strassen算法是一种特别的矩阵乘法,它通过多进行一些加法从而使矩阵乘法复杂度降低到O(nlog7)。但是算法设计还不是我们实验的主要内容。它到底性能如何,可能还要给读者留作练习。
接着我们实现基于Java的MultiThread和C的OpenMP的矩阵乘法。我们将比较两种语言在多线程并行计算下的性能差异。另外,在OpenMP实现中,我应用了SIMD技术加速我们的程序。
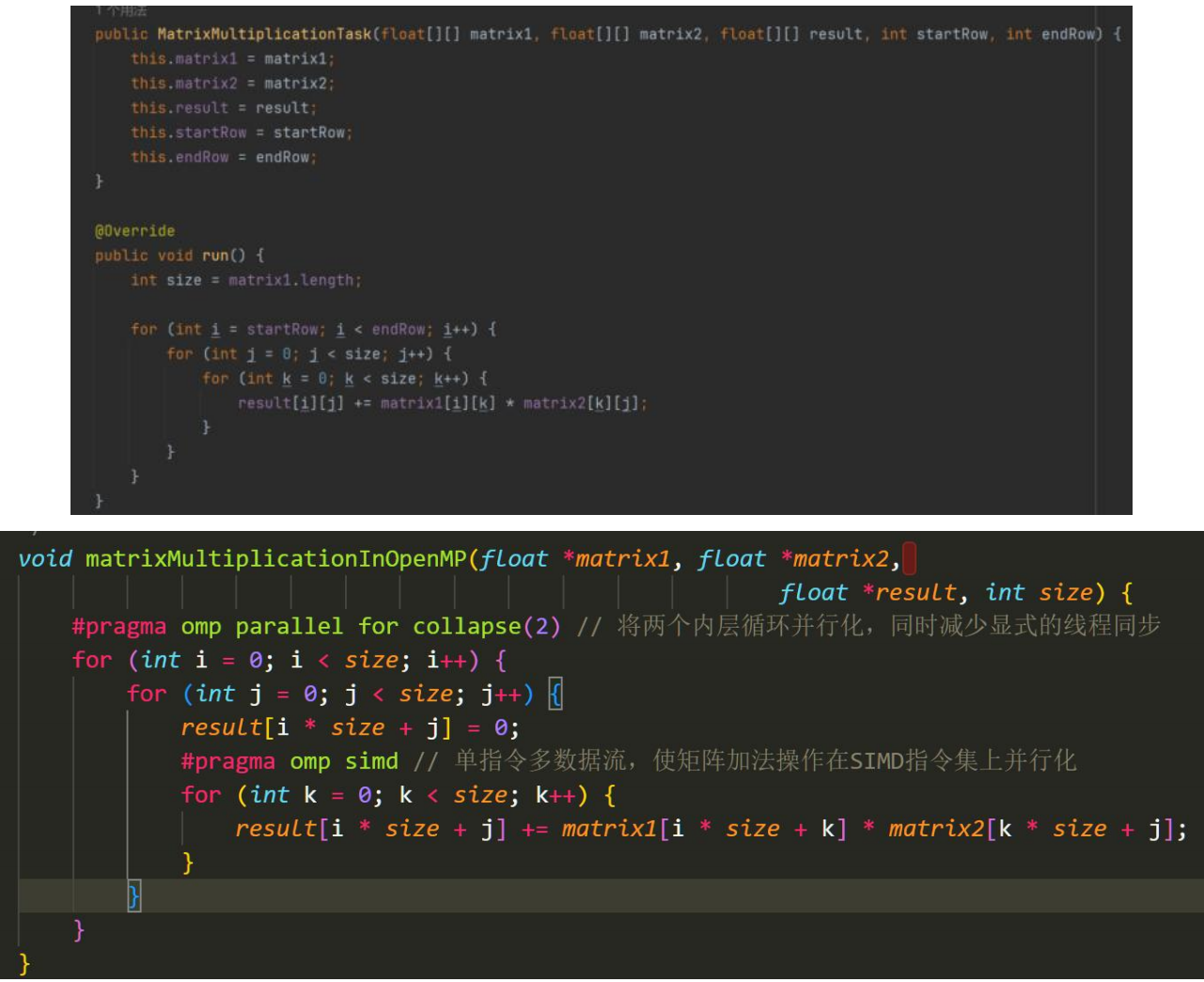
图3.5 Java多线程与C OpenMP乘法实现
最后针对CUDA,我们特地设计了矩阵乘法CUDA版本。然而很不幸的是,我们的CUDA Driver没能成功安装,所以最后我们没有实验GPU版本乘法。(我们将把这个留给读者当作练习)

Part 4: 实验设计
本次实验分为4个子实验:
实验1:运算正确性检验
首先我想确定的是,我们的算法计算出来的结果是否都是一致的,从而验证程序的运算有效性。这听起来比较基础,但是我随后发现,Java和C运算出来的结果其实并不完全一致。我们将就此给出说明。
我们将选取两个100 x 100数值区间[0,2]的矩阵进行运算,投入我们跟GPT同志一起设计的算法,比较计算结果。
| Java | C | |
|---|---|---|
| 选用算法 | 标准ijk,多线程 | 标准ijk,C OpenMP |
| 选用平台 | 试管1号,试管2号 | 试管1号,试管2号 |
| 问题规模 N | 矩阵数值区间 |
|---|---|
| 100 | [0,2] |
实验2:编译优化实验
上学期数据库的Project经验告诉我们[5],Java会有基于LLVM的JIT编译引擎,它会标记热点代码并且对热方法编译成机器码,让我们的Java运行速度越来越快。而C的编译器也有类似的编译优化,像-O2 -O3会对C编译出的机器码进行优化,比如调整分支语句、合并常量。他们的优化效果如何?我们将用内置的时间记录监测。
同样我们将选取两个100 x 100数值区间[0,2]的矩阵进行对比,查看计算结果。
| Java | C | |
|---|---|---|
| 选用算法 | 标准ijk | 标准ijk |
| 选用平台 | 试管2号 | 试管2号 |
| 问题规模 N | 矩阵数值区间 |
|---|---|
| 100,1000 | [0,2] |
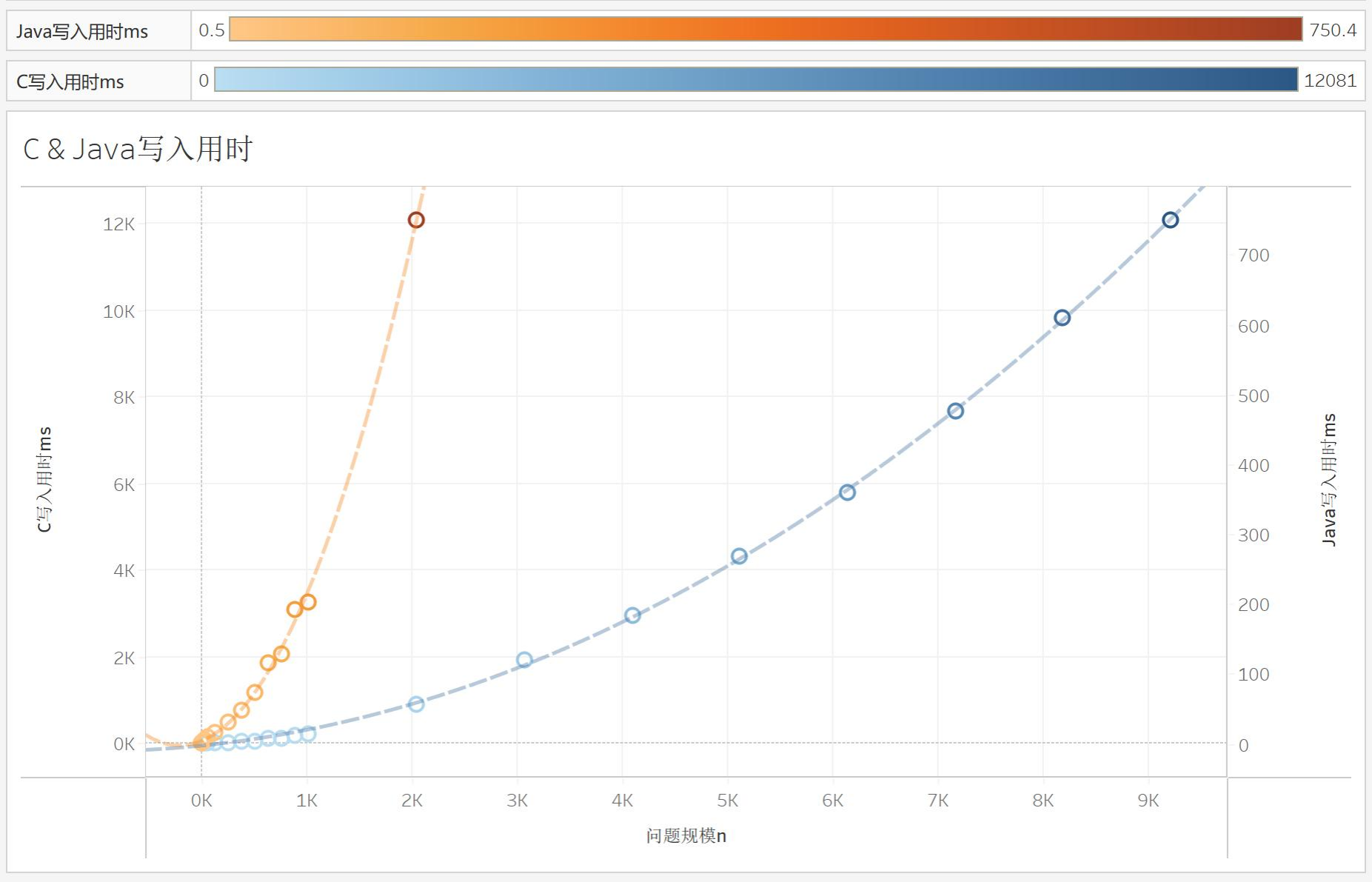
实验3:矩阵相乘速度实验 & 程序I/O实验
同样是乘法,问题规模N变大以后,谁更快?我们将记录不同算法在速度上的记录。同时,我想观察C、CUDA C和Java在I/O上的时间区别,我们将用他们内置的时间记录监测他们的读写矩阵的速度,并进行比较。我们将在试管1号试管2号上一起进行实验。
N的取值会影响我们的程序速度,同时合适的N可以让我们观察程序计算复杂度常数。再考虑电脑内存的影响,我们这次将N分为多个阶段进行比较。
| 问题规模N | 矩阵数值大小 |
|---|---|
| 2 | [-1,1] |
| 8 | [-1,1] |
| 16 | [-1,1] |
| 32 | [-1,1] |
| 64 | [-1,1] |
| 128 | [-1,1] |
阶段1
| 问题规模N | 矩阵数值大小 |
|---|---|
| 256 | [-1,1] |
| 384 | [-1,1] |
| 512 | [-1,1] |
| 640 | [-1,1] |
| 768 | [-1,1] |
| 896 | [-1,1] |
| 1024 | [-1,1] |
阶段2
| 问题规模N | 矩阵数值大小 |
|---|---|
| 2048 | [-1,1] |
| 3072 | [-1,1] |
| 4096 | [-1,1] |
| 5120 | [-1,1] |
| 6144 | [-1,1] |
| 7168 | [-1,1] |
| 8192 | [-1,1] |
| 9216 | [-1,1] |
阶段3
| 选用Java算法 | 选用C算法 |
|---|---|
| 标准ijk,Java多线程 | 标准ijk, C OpenMP |
实验4:运行时间 & 性能瓶颈实验
Java和C启动时发生了什么?JVM的启动和终止占程序的多少时间?传说中的GC对速度会有drawback吗?程序运行时的性能瓶颈在哪里,怎么分析?在CUDA C在运行时和纯C有什么区别?我们将用Profiler进行监测。
我们选取两个100 x 100数值区间[0,2]的矩阵进行对比,查看计算结果。
| 问题规模 N | 矩阵数值区间 |
|---|---|
| 100,1000 | [0,2] |
附:实验样品(矩阵)选取考虑
对于多个实验中我们选用100 x 100的矩阵,选用它有这么几个好处:
-
鲁棒性好,时间稳定,程序运算时不会因为矩阵过大或过小而出现时间范围大波动。
-
实用性好,我们的几个实验是比较语言特性,100 x 100满足我们的需求。
我们在实验中选择数值范围[0,2]和[-1,1]的矩阵,主要理由如下:
-
合适性高。float数据类型在[0,2]和[-1,1]之间的分布比较密集,可以更好地看到float的计算效果;
-
可检验性强,[0,2]的数值范围内随机选择的数的期望是1,而经过矩阵乘法运算后,结果矩阵上的数的期望为N。我们可以由此判断矩阵乘法有没有正常运行。而在问题规模N上涨后,结果矩阵上的数也跟着上涨,我们转而采用[-1,1]之间的数进行计算。
-
简化精度问题,这会在接下来的实验1结果中进行展现。
我们选择N x N的方阵作为我们算法的输入。这样有这么几个好处:
-
标准化,N x M矩阵差异比较大,我们不好准确定义问题规模。
-
简易化,让我们的程序设计更简单。我们的目标不是拿下ICPC冠军,而是比较两门语言。简单的算法可以使我们花更多的心思在性能比较上。
我们在程序速度实验中,选择N为2的幂次方及其倍数,有这么几个好处:
-
适配性好,Strassen算法需要N为2的幂次方的矩阵输入,这样才适合我们进行比较。
-
响应度高,阶梯式的问题规模可以更好地帮助我们查看程序运行速度变化情况。
Part 5: 实验结果
5.1 运算正确性实验结果
我们将相同的100 x 100的矩阵Matrix1.txt和Matrix2.txt喂给C和Java的乘法程序后,程序都成功输出了结果。表5.1.1是我们C和Java程序的输出部分结果。
首先我们发现,C和Java程序输出的结果跟在试管1号或者2号平台的运行选择无关。根据矩阵大小和[0,2]的取值范围,我们的结果矩阵内的值确实在100左右波动。同时两个算法都算出了相近的结果。
但是,可以看出,C程序计算出的所有的结果都是标准的float数值,打印出了小数点后6位。而Java则是有的是6位,有的则只有5位甚至是4位。
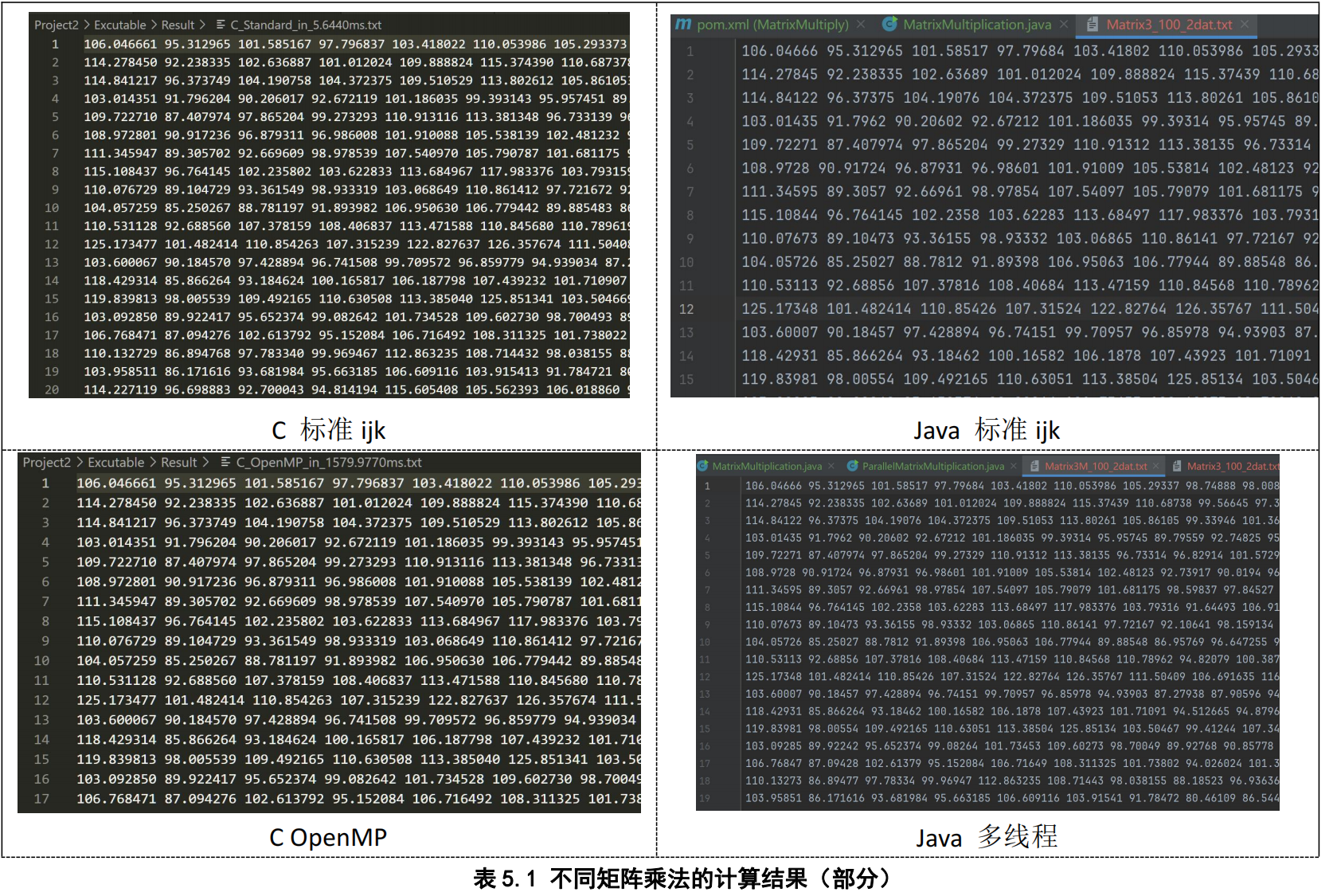
经过检查,我排除了在write或者printf上的可能性。随后在调试Java的过程中,我发现了猫腻:在计算C[0][0]的结果时,一开始数字保持着6位小数,随后随着运算的增加,突然在一次运算中就只会保留5位小数了。
我随后推测这是float精度的结果。根据Project1计算器里对IEEE754的研究,在float的指数位确定的情况下,32bit的float最多可以表示2^23 = 8388608个数字,一共七位,这意味着最多能有7位有效数字,但绝对能保证的只有6位,即float的精度为6~7位有效数字。
而在矩阵乘法中C[0][0]会等于100个float数的和。那么根据不确定度的传递公式,当两个float x1与x2相乘时,得到的新float的不确定度为:
\frac{u_{y_i}}{x_1x_2}=\sqrt{\left( \frac{u_{x_1}}{x_1} \right) ^2+\left( \frac{u_{x_2}}{x_2} \right) ^2}\ ......\left( 5.1.1 \right)
随后100个新float相加,他们的不确定度变为:
u_k=\sqrt{\sum_{i=1}^{100}{u_{y_i}^{2}}}...\left( 5.1.2 \right)
我们通过C标准库中的float.h头文件里的常量 FLT_EPSILON,查得在[0,2]之间的float数值差距约为0.0000001192。令
u_{x_i}=0.0000001192,x_i=1,y_i=1
我们得到结果矩阵的平均不确定度为:
u_k=\sqrt{100\times 2\times 0.0000001192^2}=1.68574\times 10^{-6}
通过这个理论计算,我们发现在运算后结果float的不确定度会扩大到小数点第6位。而如果考虑真实x1与x2取值会有不同,会使得公式5.1.1中x1和x2对yi的不确定度产生影响,从而使得不确定度发生变动。这可能使得不确定度大于或者小于$u_k$。这使得最后的不确定度在4-6位之间波动。
这说明,Java在计算时考虑了不确定度的影响,在计算结果上保留了结果中的精确值,省去了不确定值。但是C没有考虑,就float值的保留规则完全保留了所有的6位。我们在C中是无法感受到不确定度扩大和精度损失扩大的影响的。
同时,我们可以推导不确定度随着问题规模N和取值范围 $[l1,l2]$ 的变化公式:
u_k = \sqrt{2N} u_0 ......(5.1.3)
根据公式5.1.3,随着问题规模的增加,结果矩阵的不确定度会增加,而随着取值范围l2的增大,u_0也会随之增大。但是如果 l1,l2 之间越接近,x1和x2对yi的不确定度产生的影响会下降,最终结果矩阵里每个数的不确定度间的差距会减小。
这是我们的第一个实验,但是结果却让我出乎意料的学到了许多。虽然我们接下来要比较的主要在性能,但是不确定度的计算让我对乘法这一基本运算有了更深的认识。另外我们也得到了C和Java的第一个差别:精度保留。
那么,这个精度保留所带来的开销,会不会使Java更慢呢?还是他们仅是更高的一层抽象?这可以作为一个探索方向。
5.2 编译优化实验结果
本节实验我们选择Java和C的ijk标准程序,比较Java的JIT以及C在不优化、-O2、-O3的优化效果。
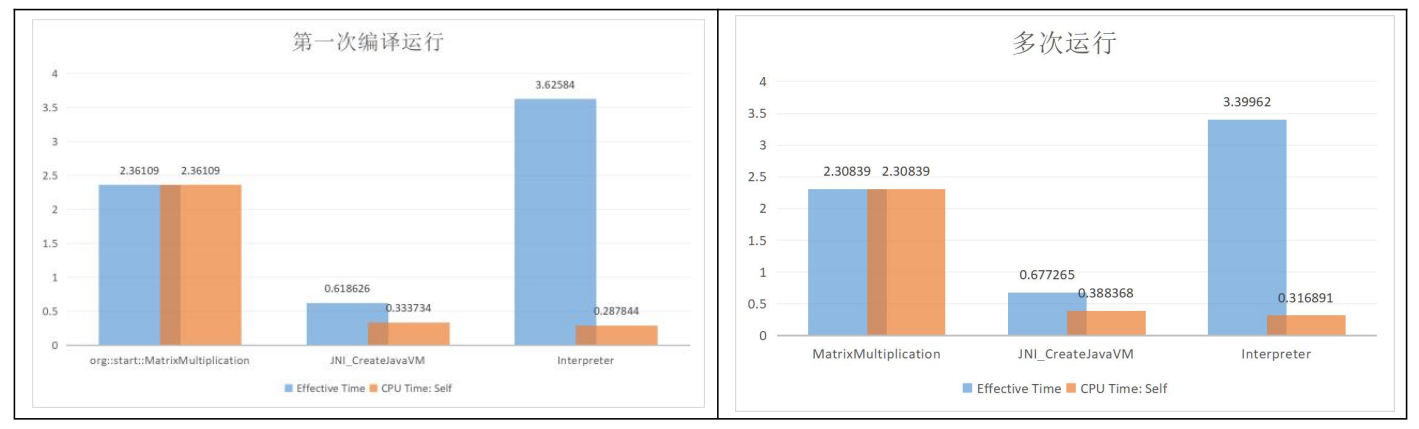
对于标准100 x 100矩阵,我们对Java执行运行第一次程序,复制文件并重复运行得到5次实验结果。之后在第一次运行后的基础上连续运行15次程序,得到多次运行程序的运算时间结果。
随后我们计算5次第一次运行程序与15次多次运行程序时间。我们可以看到,Java在读矩阵所花费的时间用时最多,而在矩阵相乘上用时最短。比较有意思的事实是写矩阵的速度是快于读矩阵的速度而非我猜测的用时相等,这应该是我在读矩阵时为了图方便用了BufferReader和正则表达式等工具导致的,他们拖慢了程序的读速度。
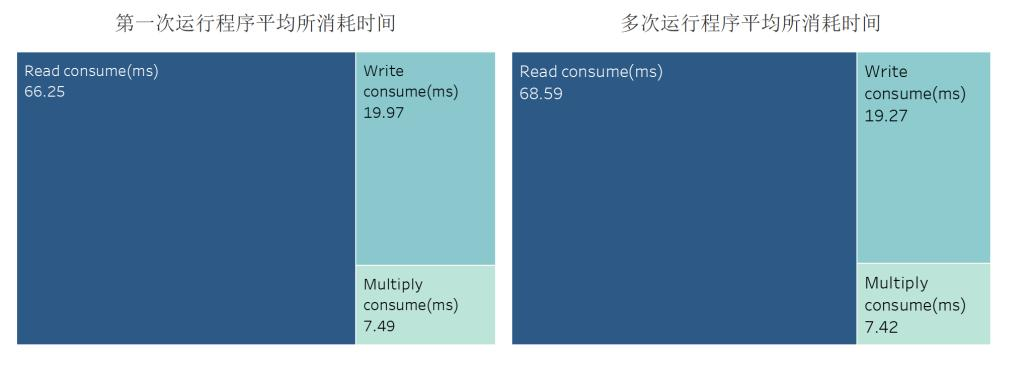
图5.2.1 Java-ijk矩阵乘法运行消耗时间
虽然在数据库的Project中我们可以清晰地发掘JIT带来的优化,但是面对基础的矩阵相乘,JIT带来的优化并不明显。
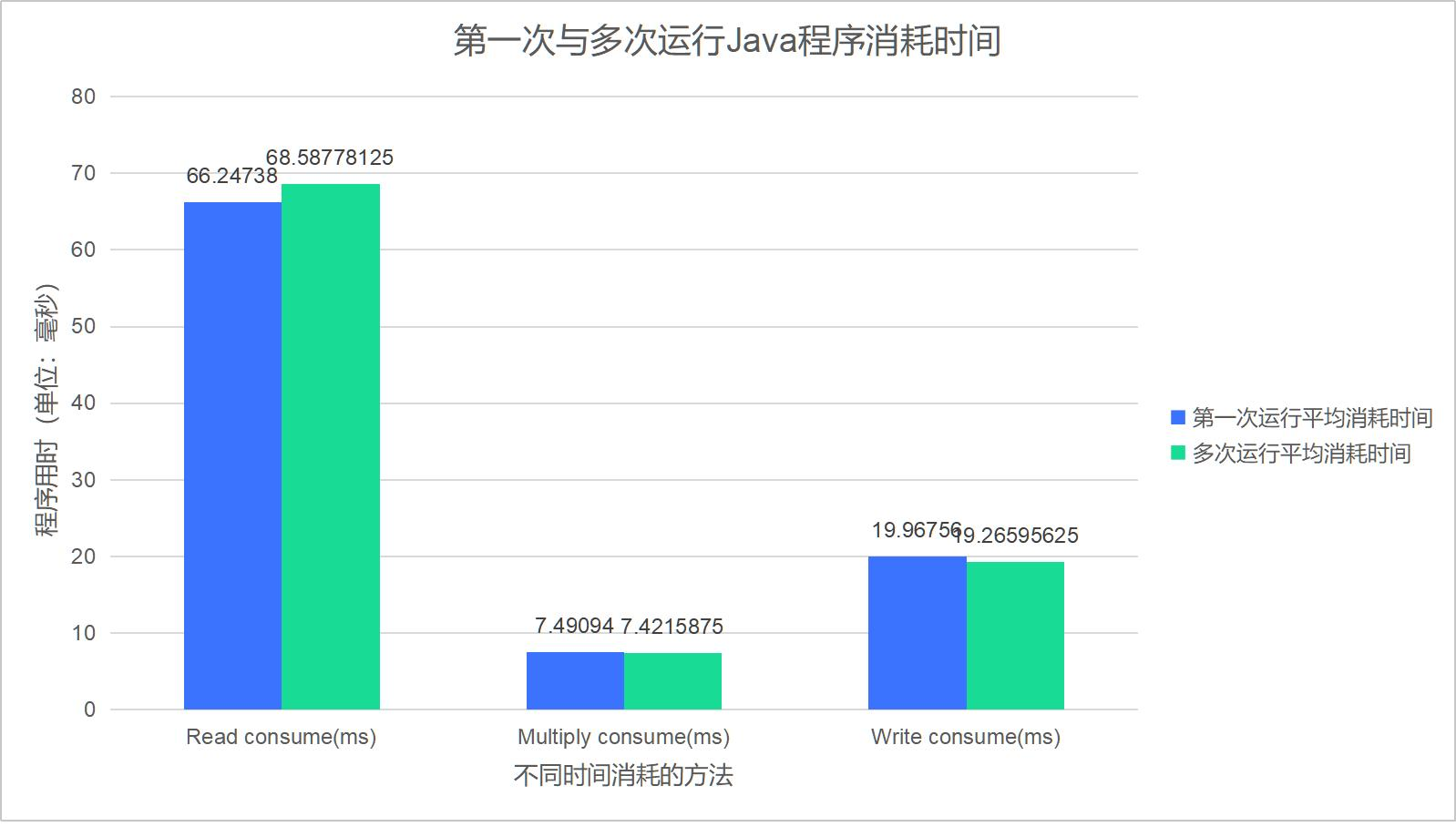
图5.2.2 Java-ijk矩阵乘法运行消耗时间对比
通过查看15次程序运行的时间,我们也发现这里边运行时间没有明显规律,三个方法的趋势线 $R^2$ 值也低于0.10,几乎没有趋势,这样的随机性说明 Java JIT 可能没有进行太多的优化。
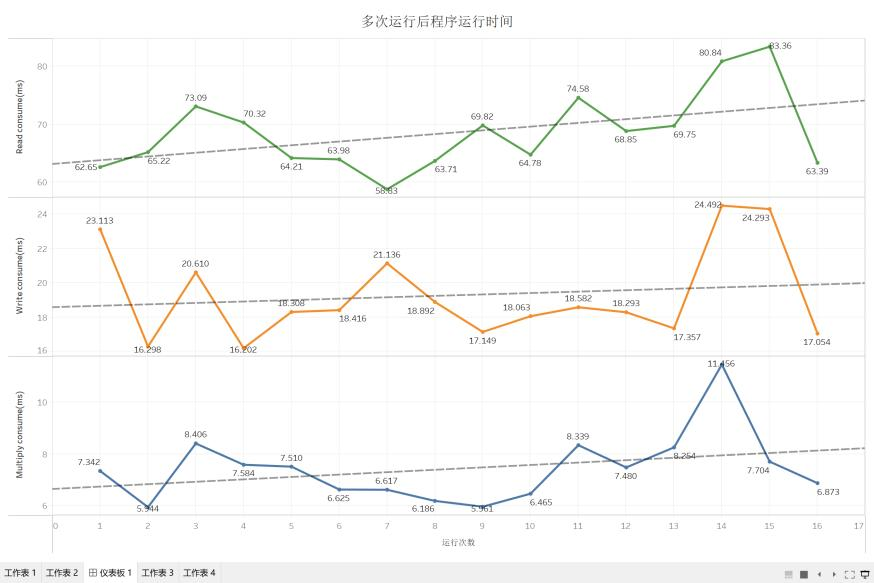
图5.2.3 Java-ijk矩阵乘法多次运行消耗时间趋势图
接下来我们测试C程序的优化效果,将普通ijk算法编译并运行10次,取程序所用时间均值。
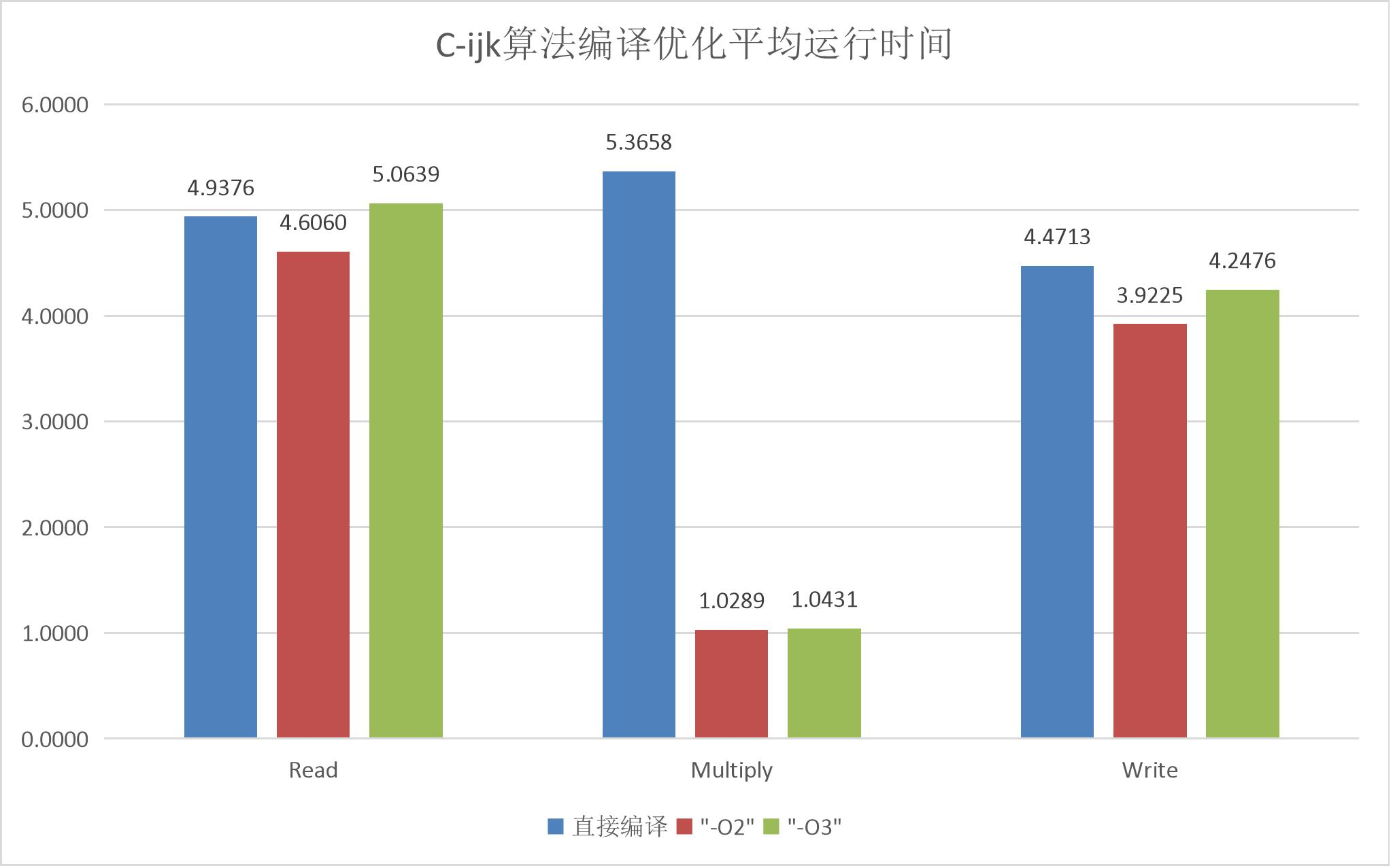
图5.2.4 C-ijk矩阵乘法运行平均消耗时间(单位:ms)
神奇的一幕发生了:虽然开启-O2和-O3选项没有明显改变I/O的所用时间,但是,矩阵乘法所用的时间迅速下降了!
这是怎么一回事?怎么JIT就做不到这样的优化?我要打开天窗一探究竟。
5.2.1 JAVA加速:JIT工作原理
在JAVA中我们一共会被编译两次:从Java到JVM看得懂的字节码,从字节码到计算机能运行的机器码。而我们的Java运行优化正是发生在字节码到机器码的过程中。
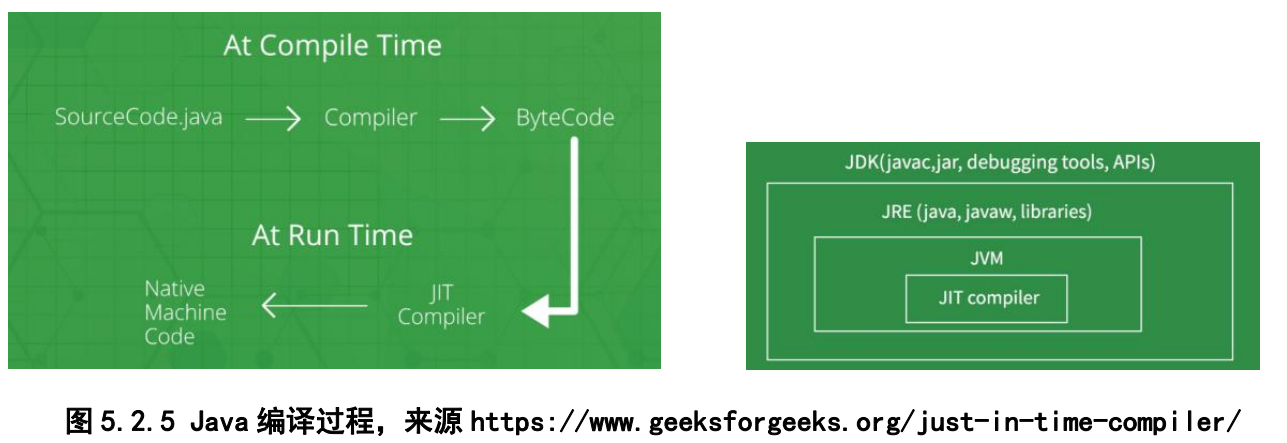
在启动Java程序时,JVM里的解释器就会开始工作。解释器会将.class文件一行一行翻译之后再运行。它不会一次性把整个文件都翻译过来,而是翻译一句,执行一句,再翻译,再执行,所以解释器的程序运行起来会比较慢,每次都要解释之后再执行。

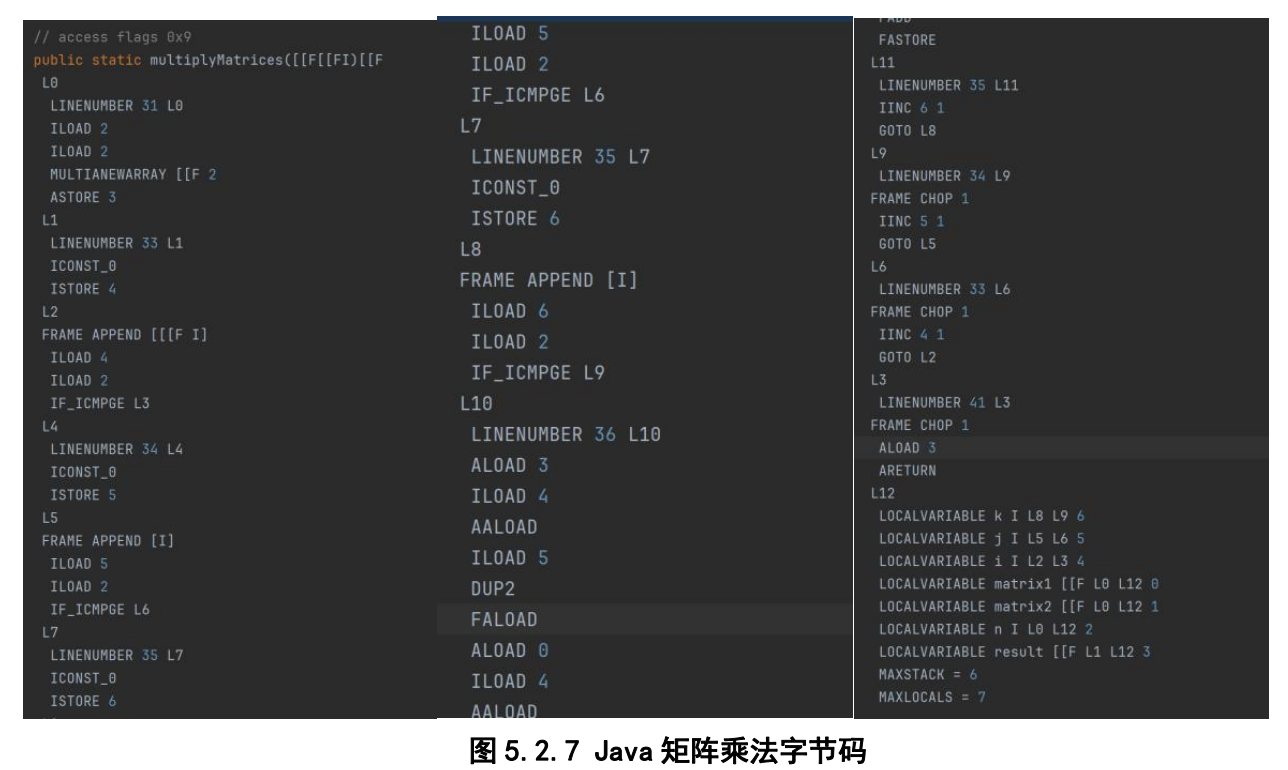
这里我找到了Javac编译出的矩阵乘法的字节码。可以看到,全程代码还是非常的长,且具体的ijk指针字节码花费了很多指令来进行。
所以,能不能把解释之后的内容缓存起来,就像数据库的缓存和CPU的缓存,就可以直接运行而不再需要解释了?但是,如果将每段代码都缓存起来,如将仅执行一次的代码也缓存起来,这太浪费内存了。由此我们引入一个新的运行时编译器,JIT来解决这些问题,加速热点代码的执行。
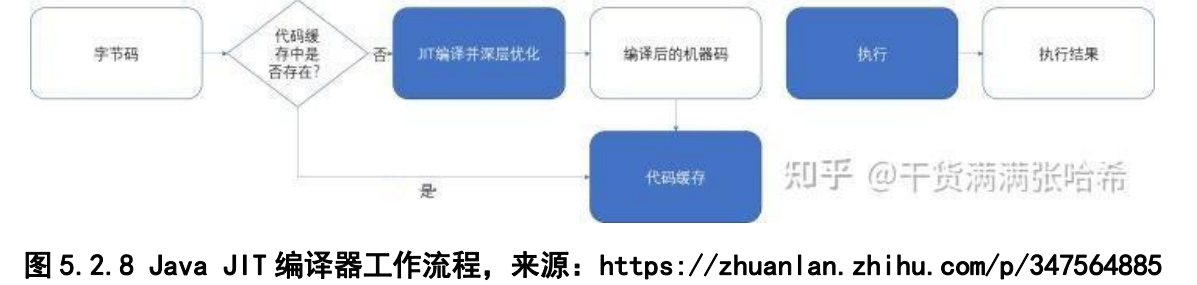
根据ORACLE官网上关于JIT的介绍,我了解到,JIT会识别程序中的热点代码,随后,将这些代码直接翻译成机器码。这样,在JVM执行机器码到热点代码时,计算机将直接执行机器码,从而提高我们程序的运行效率。

而热点代码、热方法的选择算法不同的JVM有不同实现,如基于方法,基于踪迹,基于区域。我们平时遇到的最典型的基于方法的JIT中,一般探测热点方法有基于采样的热点探测,即周期性的去检查线程的调用栈顶,如果方法经常出现在栈顶,那它就是热点方法。这个操作有点像我们Profiler去监控程序。另一种是基于计数器的热点探测,这种会给每个方法建立计数器,用来统计方法的执行次数。超过阈值的就认为是热点方法。

而在对于检测出的热点代码,编译器也分为了两种:C1,C2。由于历史原因,C1也被称为客户端编译器,C2被称为服务器编译器。与C1编译器相比,C2编译器对性能要求更高,会对代码做更加深层的优化,相应的也会比C1编译的时间更长。JVM会根据代码情况,执行时间情况动态地选择C1,C2编译器。由于JVM会动态推测热点代码,假如一段代码使用了一段时间后不再是热点代码了(比如先读取矩阵,后面就不再使用此方法),JIT可能会执行“去优化”,将停止执行编译的代码以切换到更慢的解释代码。
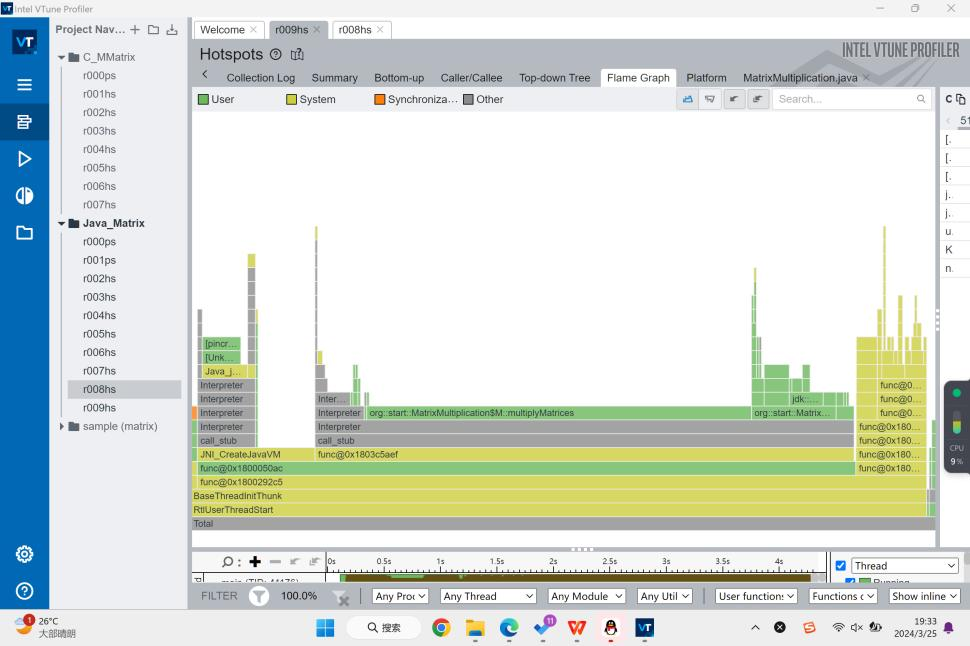
理论了这么多之后,我们来看在实际过程中JIT的执行结果。在第一次执行Java的时候,我们看到,编译器花了许多时间对程序进行编译,然后再运行编译好的代码。而这些编译的代码是动态的,他们在执行我们的读写函数时(根据用时判断应为func@0x180003bd0等函数)边进行编译。而对矩阵乘法函数的编译则出现的比较靠后,并且我们看到是在call_stub函数后进行编译的,我推测这个函数便是JIT检测热点代码的函数。同时我们可以看到,大部分System层面的运行都是在维持JVM的运转,程序在开始CreateJavaJVM和结束时调用了很多方法和线程。
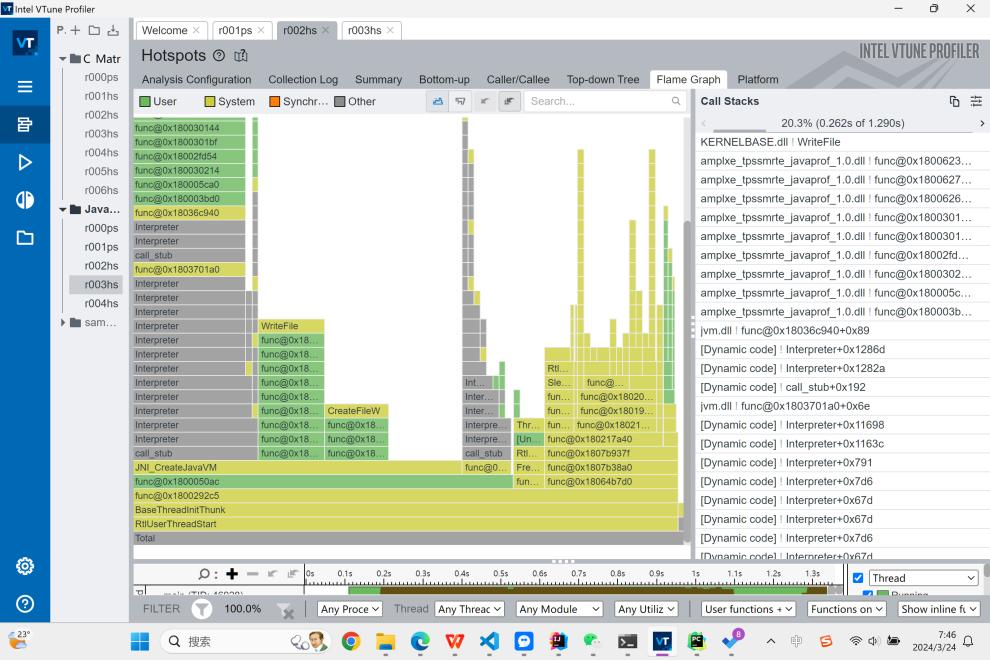
事实上我们也可以看到,在第一次运行中程序在启动JVM上的时间反而是占比最多的。当然这也和我们的矩阵规模选取有关,一旦规模增大,在方法上所耗用的时间应还是最多。
这里我们选择的矩阵规模为100 x 100,可能还有很多参数Profiler来不及收集,于是我们决定选择一个1000 x 1000的矩阵。
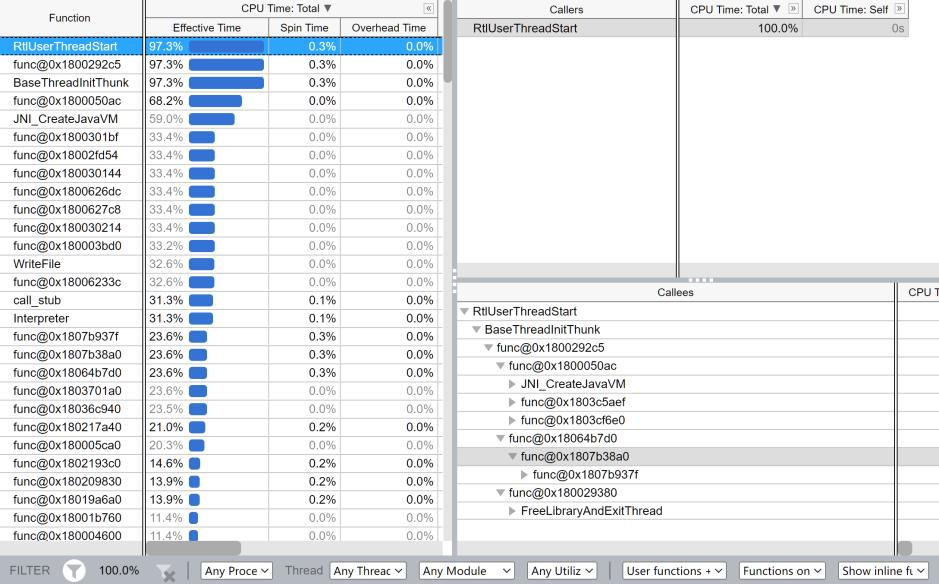
在1000 x 1000矩阵的输入下,程序将大部分时间花在了运算上,不过CreateJavaJVM,Interpreter还是占用很多时间,接近0.6秒。 另外一个比较有趣的观察是,JVM有会有自己的数学库:jdk::internal::math。
同时,JVM还是会先进行编译,然后在我们的程序执行过程中动态地编译程序。这里我将第一次运行的程序热力图放在左边,多次运行的程序热力图放在右边。可以看到,程序运行的基本流程是大致相同的,但是多次运行的程序会省略掉部分子程序,有部分程序会被提前执行、更多精细的程序会被调用等等。
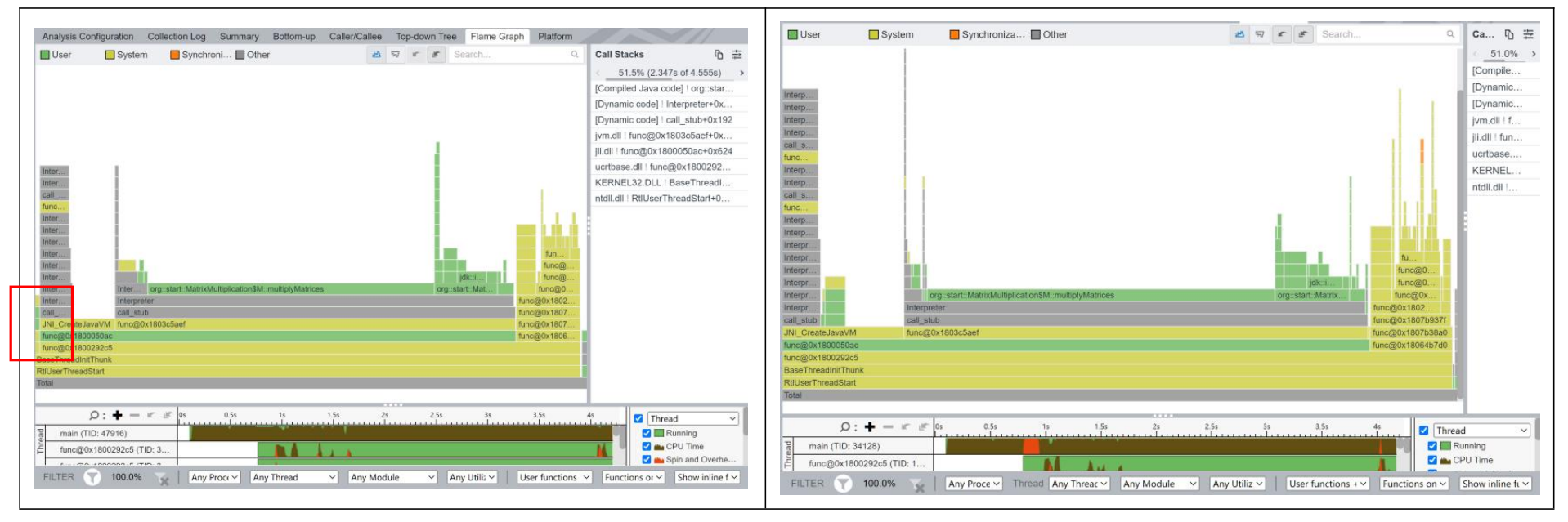
在多次运行的情况下, 程序编译的有效时间减少了,矩阵乘法的运行速度也有了微量提升。
我还是最关心 MatrixMultiply 方法被编译成了什么。在这里我们成功地查看到JVM翻译出的汇编代码层。我们可以看出,虽然在执行时间上差距不大,但是汇编层面......居然也没有优化,并且全是奇妙的caller callee指令。我在这里用了多种方法,尝试让编译器重复计算MatrixMultiply,但是很遗憾的,所有的尝试JVM出来的汇编代码都是一样的。也就是说我们的JIT优化对于我们的矩阵乘法效果上在汇编层面没有优化汇编。
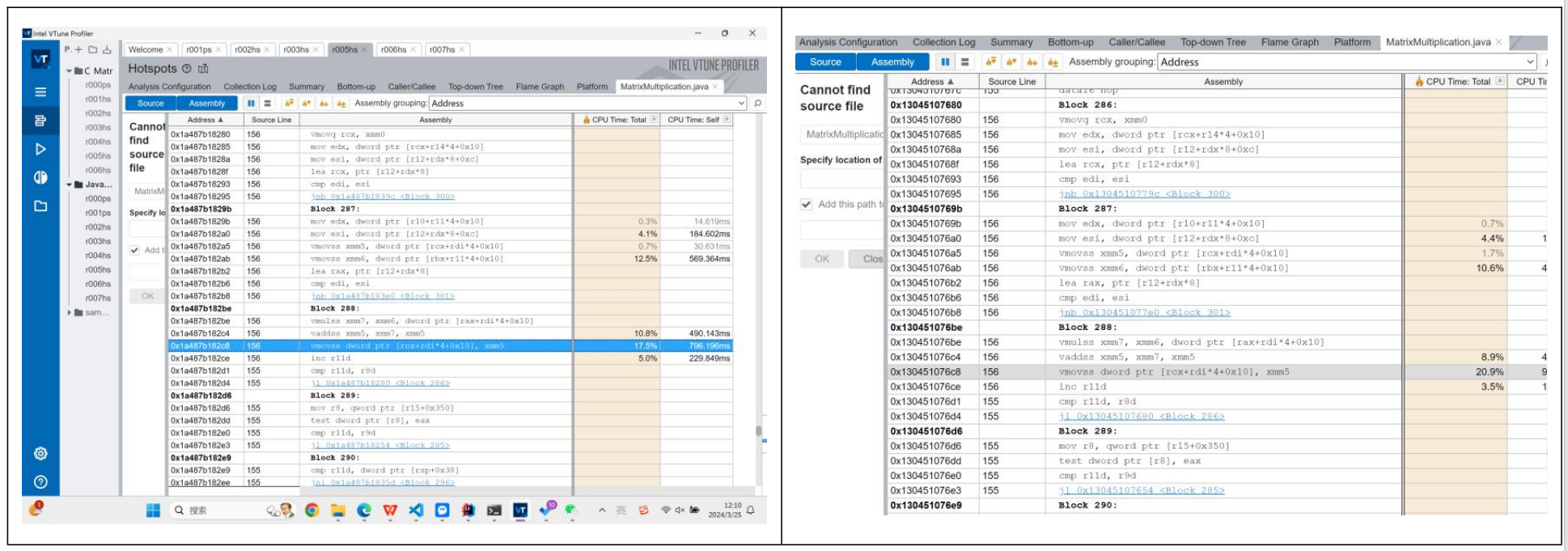
5.2.2 C 编译加速:-O3到底做了什么?
我们接下来查看C的矩阵乘法的效果。由于C在运行100 x 100时太高速了,Profiler没有捕捉到程序的太多信息。于是我也给它投喂了1000维的矩阵,查看运行的信息。左边的表格是标准编译,右边则是使用了-O3进行了编译。
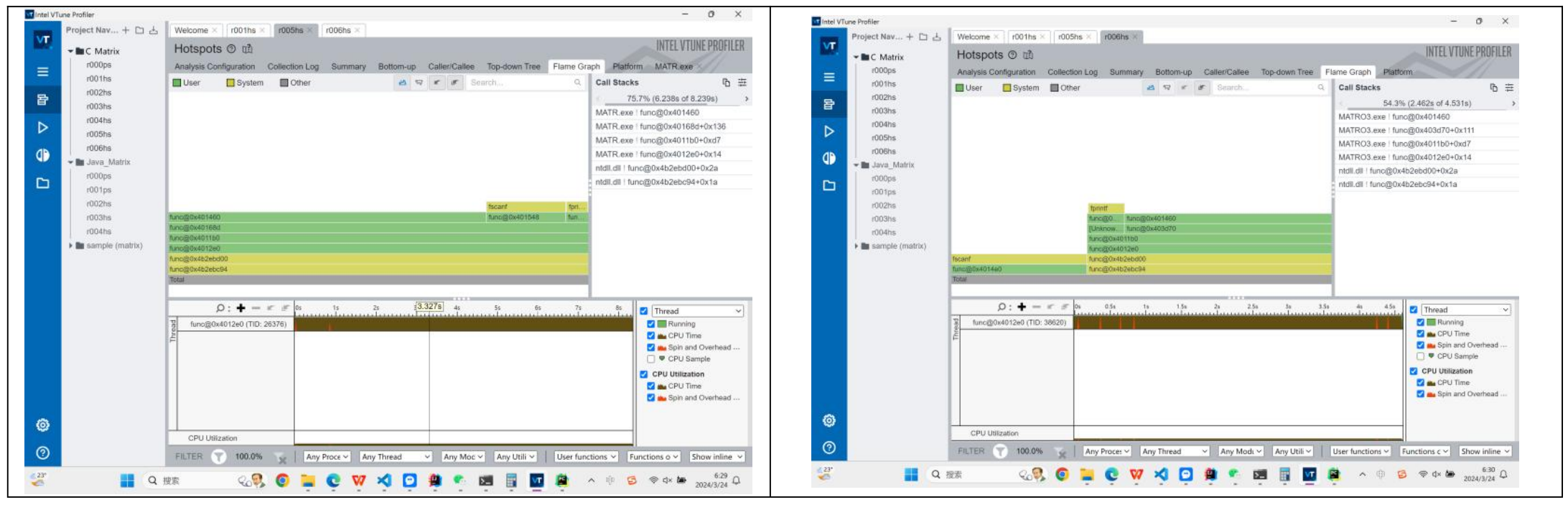
我们可以看出,跟Java的复杂比起来,C的代码执行的就很干脆利落。并且,编译带来的优化是显而易见的,连程序运行的结构都发生了改变。
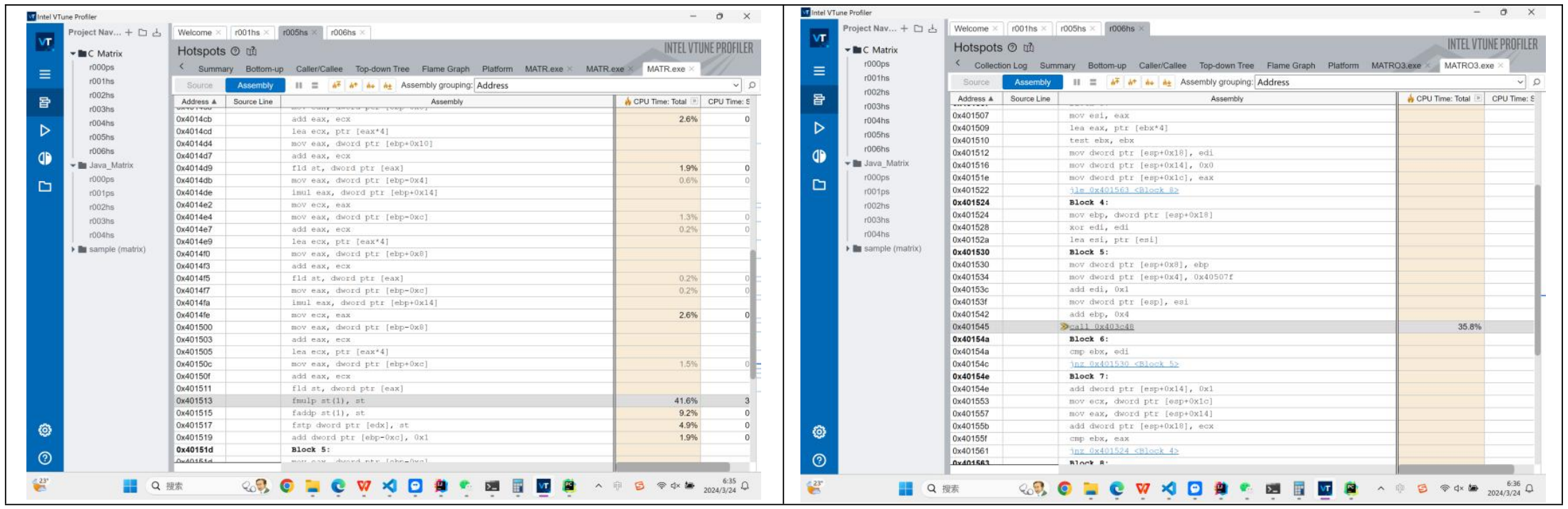
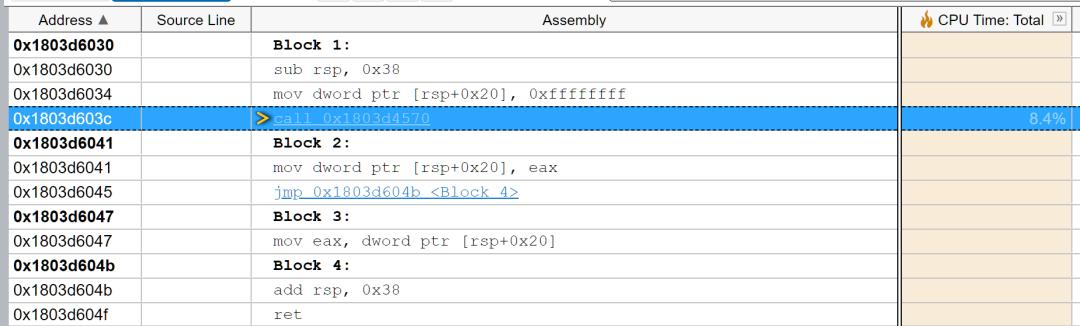
我们接下来找到并对比MatrixMultiply的部分汇编代码。可以看到,最多优化的就是代码Block4。我们可以把block4的代码copy下来进行分析:
首先是直接编译,根据计组的知识我们可以知道,mov是移动,eax,edx是x86上的寄存器,dword是double word,lea是装载有效地址,fld是加载浮点数到寄存器,imul是执行有符号乘法,fmulp,faddp是浮点数的乘法和加法。黑色字体的注释是我写的。(啊,感谢计组)
Address Source Line Assembly CPU Time: Total CPU Time: Self
0x4014a5 Block 4:
0x4014a5 mov eax, dword ptr [ebp-0x4] 2.1% 0.170s
0x4014a8 imul eax, dword ptr [ebp+0x14] 0.2% 0.016s
0x4014ac mov edx, eax
0x4014ae mov eax, dword ptr [ebp-0x8]
0x4014b1 add eax, edx 1.9% 0.156s # eax = edx
0x4014b3 lea edx, ptr [eax*4] # edx = eax * 4 目的是得到地址i
0x4014ba mov eax, dword ptr [ebp+0x10]
0x4014bd add edx, eax
0x4014bf mov eax, dword ptr [ebp-0x4] 2.1% 0.171s
0x4014c2 imul eax, dword ptr [ebp+0x14]
0x4014c6 mov ecx, eax
0x4014c8 mov eax, dword ptr [ebp-0x8]
0x4014cb add eax, ecx 2.6% 0.217s
0x4014cd lea ecx, ptr [eax*4] # ecx = eax * 4 目的是得到地址j
0x4014d4 mov eax, dword ptr [ebp+0x10]
0x4014d7 add eax, ecx
0x4014d9 fld st, dword ptr [eax] 1.9% 0.154s
0x4014db mov eax, dword ptr [ebp-0x4] 0.6% 0.047s
0x4014de imul eax, dword ptr [ebp+0x14]
0x4014e2 mov ecx, eax
0x4014e4 mov eax, dword ptr [ebp-0xc] 1.3% 0.109s
0x4014e7 add eax, ecx 0.2% 0.016s
0x4014e9 lea ecx, ptr [eax*4] # ecx = eax * 4 目的是得到地址k
0x4014f0 mov eax, dword ptr [ebp+0x8]
0x4014f3 add eax, ecx
0x4014f5 fld st, dword ptr [eax] 0.2% 0.016s # 加载st matrix[i][k]
0x4014f7 mov eax, dword ptr [ebp-0xc] 0.2% 0.016s
0x4014fa imul eax, dword ptr [ebp+0x14]
0x4014fe mov ecx, eax 2.6% 0.214s
0x401500 mov eax, dword ptr [ebp-0x8]
0x401503 add eax, ecx
0x401505 lea ecx, ptr [eax*4]
0x40150c mov eax, dword ptr [ebp+0xc] 1.5% 0.125s
0x40150f add eax, ecx
0x401511 fld st, dword ptr [eax] # 加载st matrix[k][j]
0x401513 fmulp st(1), st 41.6% 3.424s # st = matrix[i][k] * matrix[k][j]
0x401515 faddp st(1), st 9.2% 0.761s # result = result + st
0x401517 fstp dword ptr [edx], st 4.9% 0.406s
0x401519 add dword ptr [ebp-0xc], 0x1 1.9% 0.156s这段代码比较长,但是其实不难理解或者猜测它的行为。结合GPT,大概是这样的:ebp是我们的基址指针,在x86架构中,通常使用基址指针来帮助访问栈上的局部变量和函数参数。随后,我们在栈上存储了我们矩阵的ijk三个循环变量,matrix1,matrix2,result的基地址。我们依靠ebp取出matrix[i][k]和matrix[k][j],然后使用fmulp和faddp完成矩阵的乘法。
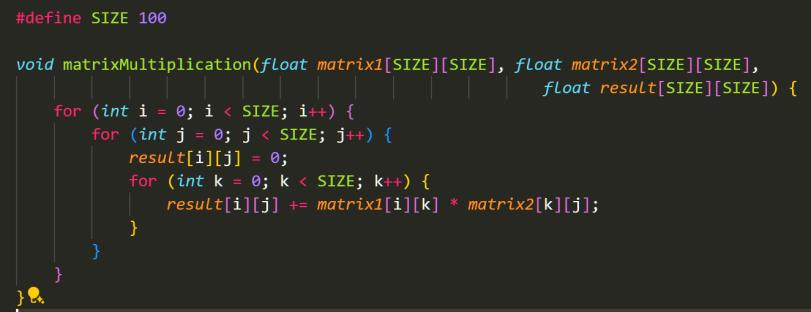
这段代码从注释上可以看到,它是有冗余的,比如在得到地址ijk上前面的步骤非常的多。当然,它不失为一种好方法,毕竟这种方法算是翻译了C语言,如果在计组课上这可能会被当成一个example。
我们再来看看开了-O3后编译器编译出的汇编代码:
Address Source Line Assembly CPU Time: Total CPU Time: Self
0x401492 Block 4:
0x401492 fst dword ptr [ecx], st
0x401494 mov edx, edi
0x401496 xor eax, eax
0x401498 fld st, st(0)
0x40149a lea esi, ptr [esi] # 矩阵
0x4014a0 Block 5:
0x4014a0 fld st, dword ptr [ebx+eax*4] 7.5% 0.339s # 加载第一个矩阵元素到浮点寄存器栈中的栈顶
0x4014a3 add eax, 0x1 # 将 eax 加 1
0x4014a6 fmul st, dword ptr [edx] # 将栈顶的浮点数与地址为 edx 的浮点数乘起来
0x4014a8 add edx, esi 31.3% 1.416s # 将 edx 加上 esi
0x4014aa cmp ebp, eax 1.4% 0.062s # 将 ebp 与 eax 进行比较
0x4014ac faddp st(1), st # 将栈顶的两个浮点数相加,并弹出栈顶的浮点数
0x4014ae fst dword ptr [ecx], st 12.2% 0.555s # 将栈顶的浮点数存储到地址为 ecx 的内存中
0x4014b0 jnz 0x4014a0 <Block 5> 2.0% 0.091s # 如果比较结果非零,则跳转到 Block 5,否则继续执行下一条指令,这里应该是比较的是k和size
0x4014b2 Block 6:
0x4014b2 fstp st(0), st
0x4014b4 add ecx, 0x4 # ecx是地址,地址+=1,应该是i,代表matrix1的i行
0x4014b7 add edi, 0x4 # edi的地址+=1应该是j,代表matrix2的j行
0x4014ba cmp ecx, dword ptr [esp]
0x4014bd jnz 0x401492 <Block 4> # 回到block4这段代码就没有那么直白,但是通过仔细分析我发现,-O3确实是在ijk循环上面下了功夫,直接把原本栈上的ijk,SIZE变量直接存储在CPU的寄存器上,减少了我们的I/O
读写次数,同时,add ecx 0x4这个操作也简化了地址的效率。这样,不仅是我们的总指令数IC(Instructions Count)减少了,因为我们简化了取地址和指针的汇编程序。而且,我们的平均CPI(Clock cycles per instruction)也减少了,因为我们向栈内存上的访问次数减少了。
根据计组里的CPU性能估算公式,对于一个程序,它的运行时间跟IC,CPI和时钟频率挂钩。在CPU时钟频率不变的情况下,IC的下降,不用执行那么多程序,那我们的程序运行时间也就下降了。
CPU\ Time\ =\ Instruction\ Count\left( IC \right) \ \times \ Cycles\ per\ Instruction\left( CPI \right) \ \times \ Clock\ Period\left( T_c \right)
这里一个有趣的问题是,CPI会下降吗?
我做实验2时,我认为既然开了O3,指令执行的时间应该也变短了,那CPI应该会下降。但是,当我在做实验4时我发现,真实情况是IC下降,CPI上升了,不过由于-O3指令的优化,所以总时钟周期数下降了,才导致了整个CPU Time下降了。我在这里做了一个错误的猜测)
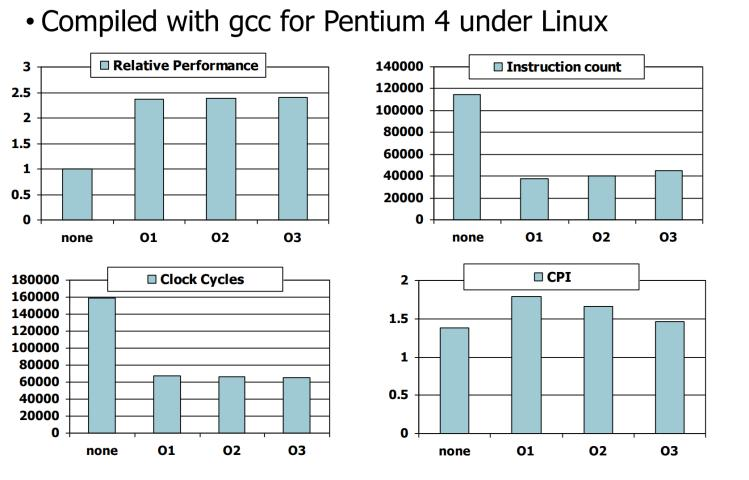
我们可以根据教科书上的图片来看看CPI是否提升,以及编译器优化的效果。
当然,这里我也尝试-O2的效果,这里编译出来的结构和-O3完全一致,如果比较汇编,会发现代码结构也基本一致。
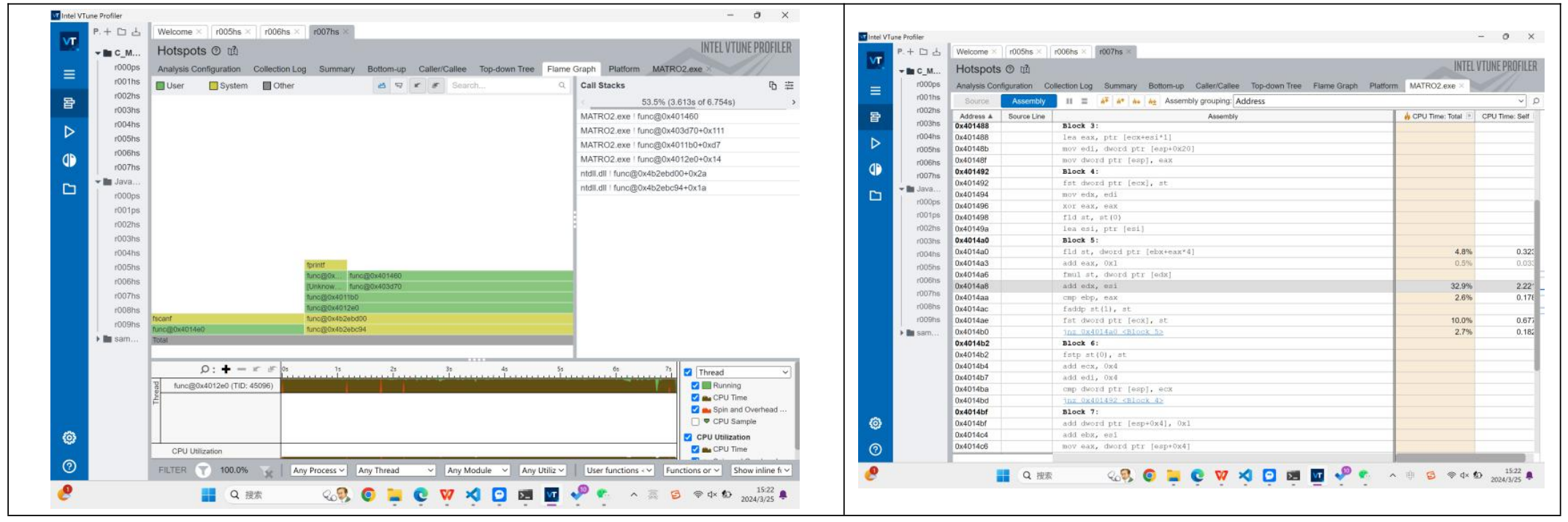
比较不同的汇编代码在于Block 6,-O2导入的还是dword到寄存器中,但是到-O3就直接存储的是指针ecx。可以看出,-O3会优化到极致,能用寄存器就用寄存器,可以用指针就用指针。

在CSDN上这篇文章:#linux# gcc编译优化-O0 -O1 -O2 -O3 -OS -CSDN博客,给出了-O0,-O1,-O2,-O3的优化范围。比如下面是-O2的优化范围:

我们在刚刚的-O3的汇编中已经感受到了这两个优化,对栈指令的优化,数据拷贝中寄存器访问的减少和ijk循环变量的优化。除此之外,-O2还会执行课上老师所讲的inline操作,将小方法内联到我们的大方法中,优化取指令的操作。
而在-O3下,gcc会执行下面这个优化,我推测这是我们block6汇编改变的原因。

所以,通过这个实验,我深刻地从最基层的体验到Java和C在执行层面上的区别。Java会启动JVM并且进行及时编译运行代码,这里边要启动JVM的各种线程。JIT计算会对热点代码进行C1或者C2编译以提升Java的运行速度。然而可惜的是Java面对矩阵乘法,JIT在汇编指令上的优化是有限的,因而其所在乘法算法上做的优化很有限。但是C语言中gcc的汇编指令上的优化是明显的,它会尝试减少程序的汇编指令数,尝试减少花费高昂的内存读取指令的次数,尝试用指针代替实际的word,减少程序的IC和CPI,从而减少程序的运行时间。
同时我们也知道,JVM是在边编译边执行机器码,这样其实是占用了程序一定的时间,并且这些编译在有时并没有取到非常好的效果,他们的汇编代码没有gcc编译出的那么优化。而这是我认为在乘法程序执行上Java会比C缓慢的一个重要原因。
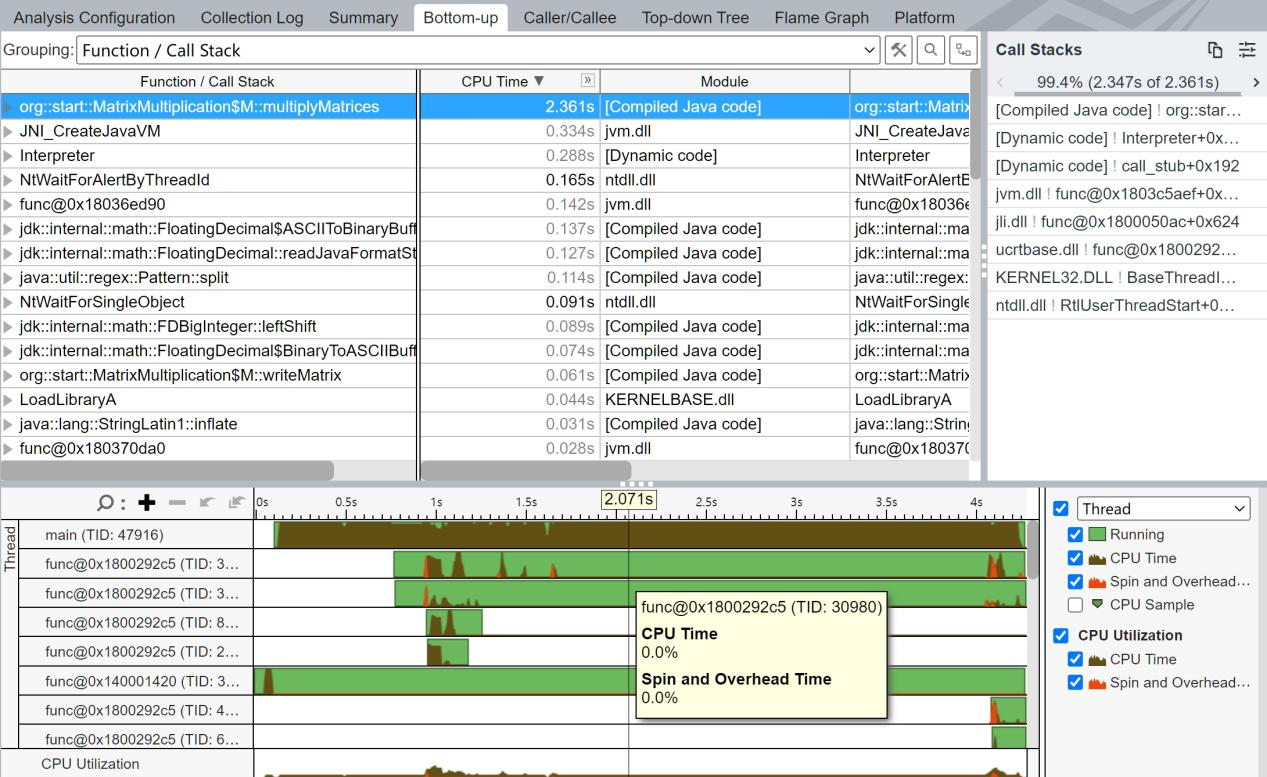
5.3 矩阵相乘速度实验 & 程序I/O实验结果
我们将21个矩阵案例输入到我们的Java和C程序中,分别在我们的试管1号和试管2号上运行。最终得到了我们的测试结果。我们将查看程序中矩阵乘法的消耗时间。
这里我们的试管2号由于系统限制,JVM的内存不能开太大。我们就暂时测量到N=2048的矩阵。

矩阵乘法复杂度实验
我们先来分析一下试管1号的程序结果。受到数据的影响,我将问题规模取了对数log(N),程序用时也取对数进行分析,得到下面的乘法用时图。
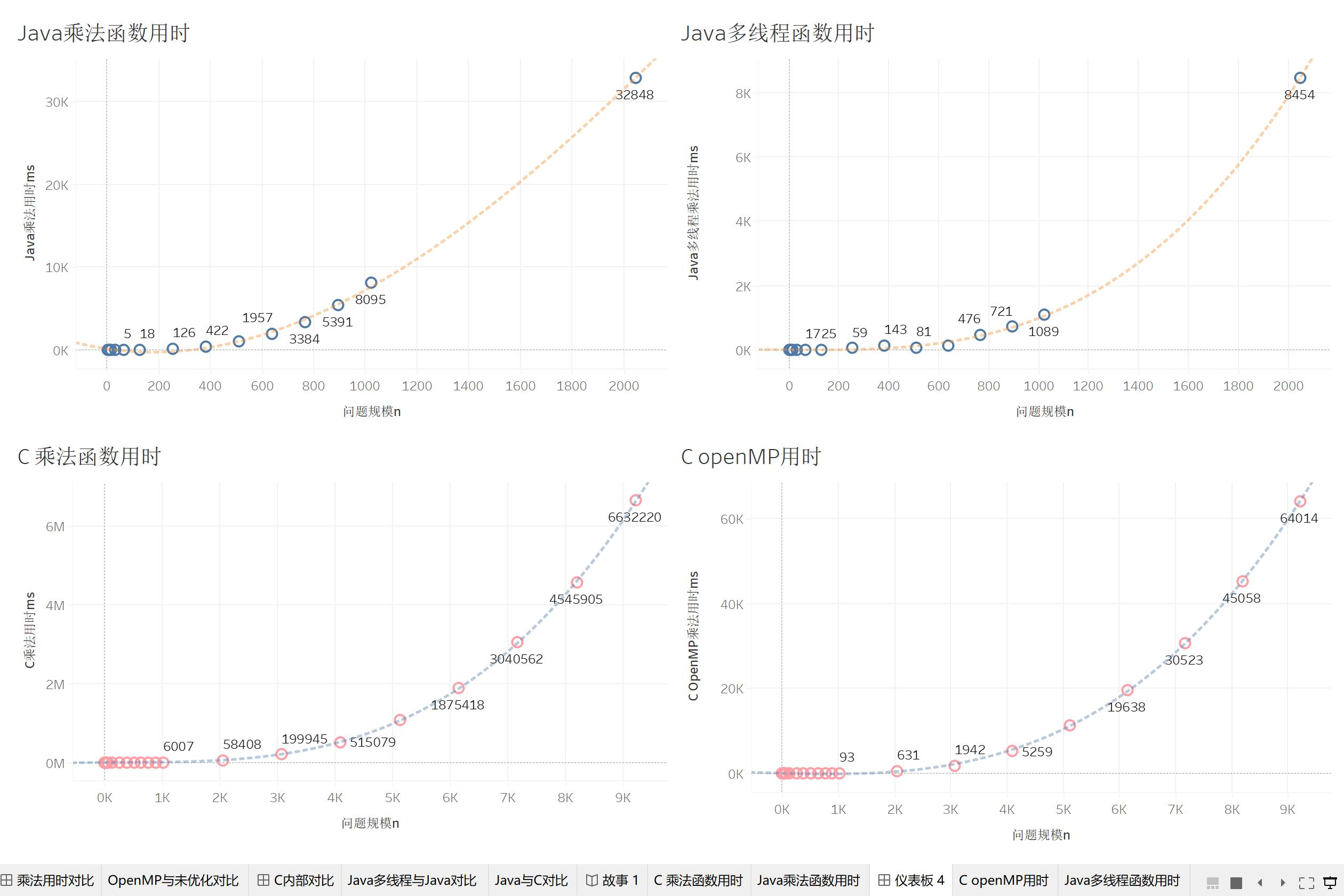
我们用 N^3 曲线去拟合我们的时间-矩阵维数散点图,得到的 R^2 值均在0.999以上,P值小于0.001。说明我们的函数的计算复杂度都在 O(n^3),符合理论。而像读取和写入矩阵,使用 $N^2$ 可以得到很好的拟合效果,这也说明我们的读写的复杂度就在O(n^2)。
多线程矩阵乘法速度实验
在对数据处理时,开始时我并没有选择直接将数据展现成图表。我是先对我们的问题规模和用时取了对数,然后做成了下图:
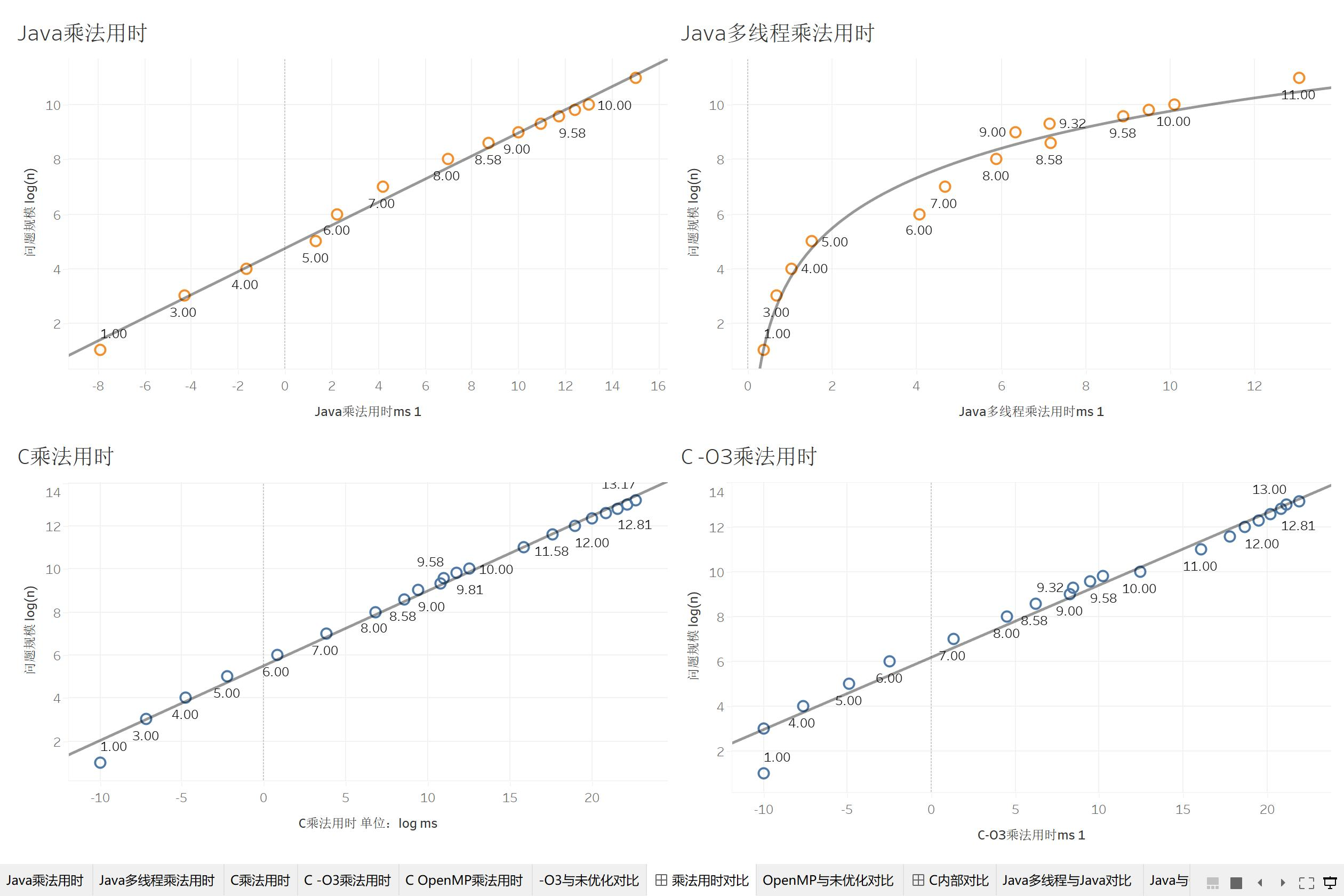
从图中我们可以得知,C乘法,C-O3乘法,Java乘法的程序运行时间都满足
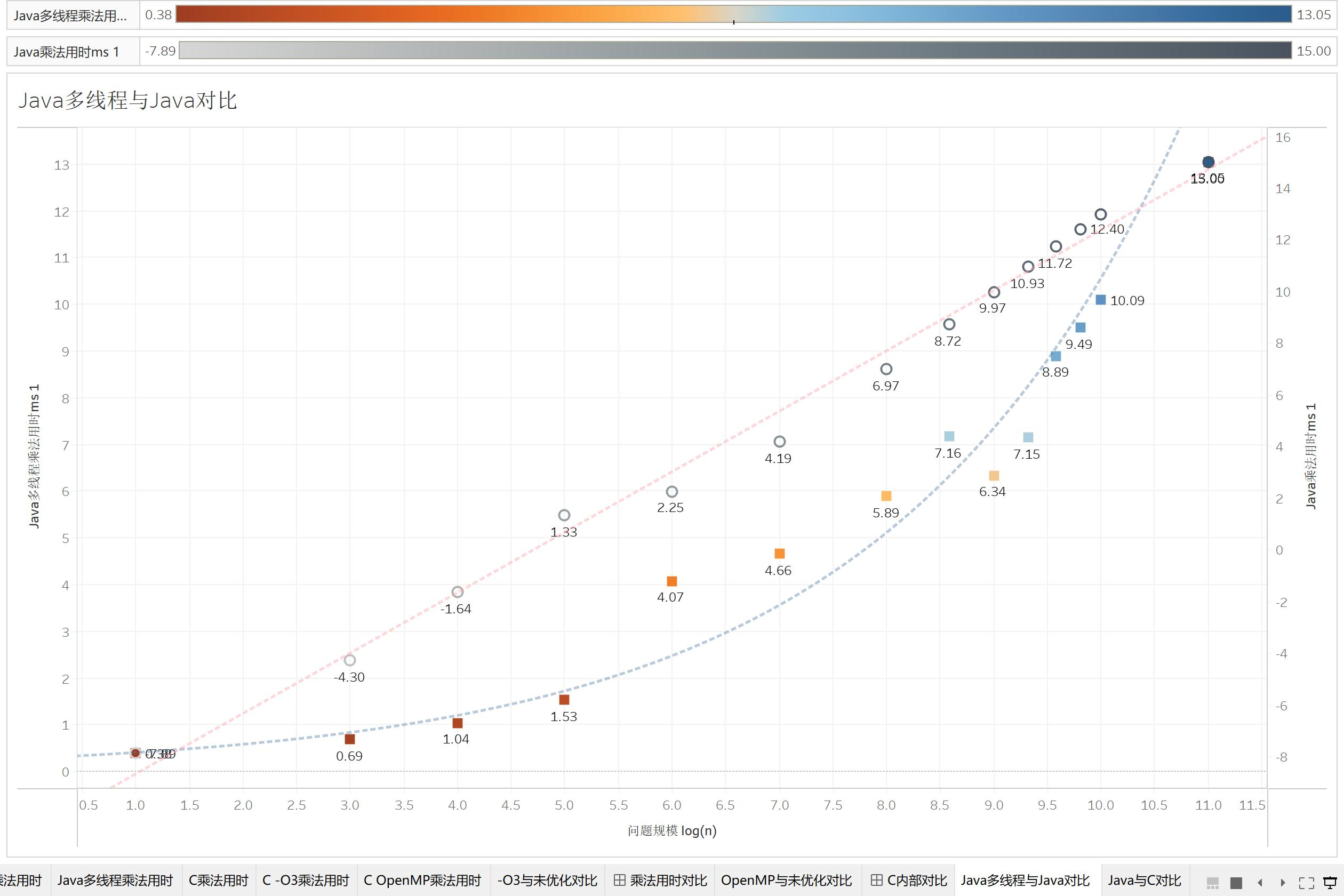
\log \left( T\left( N \right) \right) ~-~ \log \left( N \right),这是可以根据刚刚的公式推出来的。但是,我们继续测量出多线程下两者的用时,我们发现,Java多线程在两者log之后,问题规模增加,乘法的用时增长率更大了。
类似的事情也发生在OpenMP上,它也不是一个简单的直线而是一个偏对数偏三次函数的曲线。这说明,在经过并行处理后的程序,他们因为并行,这当中造成的延迟、数据传输,使得最终程序用时不再是一个明显的三次函数曲线。
我们可以看到,执行了4个线程的Java程序,它的计算时间是一定大于原来程序的四分之一的。但是具体大多少,这和通信有关。而我们目前的发现是可以展现出Java语言和C语言在多线程技术下的CPU间通信开销,我们甚至可以使用阿姆达尔定律来计算它们的加速比。(给读者留作练习)
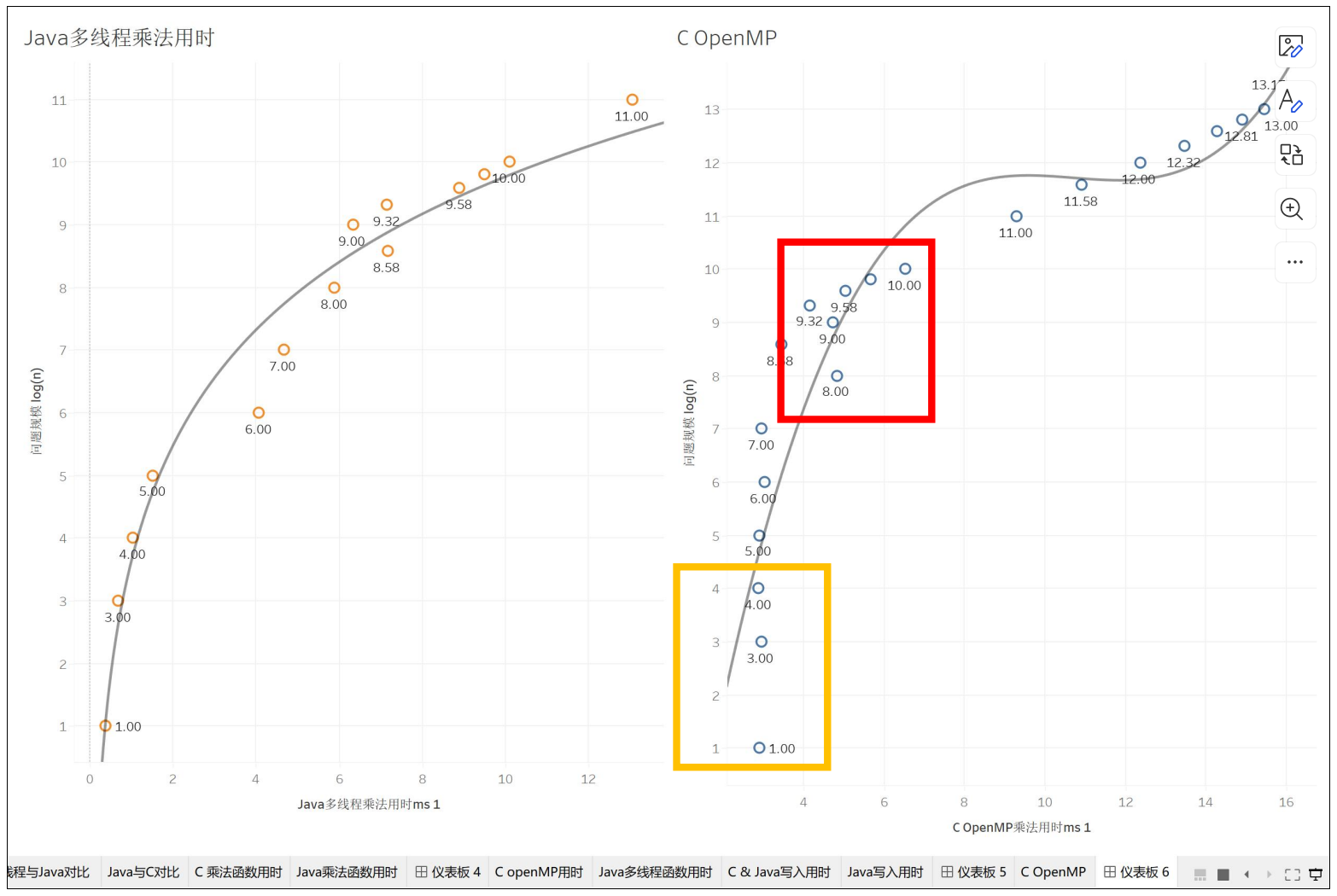
另外值得一提的是我对OpenMP的推测。OpenMP在单核情况下是没有特别多通信阻碍的,但是一旦多核起来就会增加一层L3缓存上的开销,使得程序运行时间发生突变。我认为这是在上图中的橙色方框里发生的过程。而我们的OpenMP是在1号服务器上进行的测试,它有两个CPU构成NUMA节点。当我们的OpenMP需要让CPU0和CPU1在内存上进行通信时,NUMA架构会使程序的运行时间发生第二次突变,而我认为这就是上图中红色方框发生的事情。
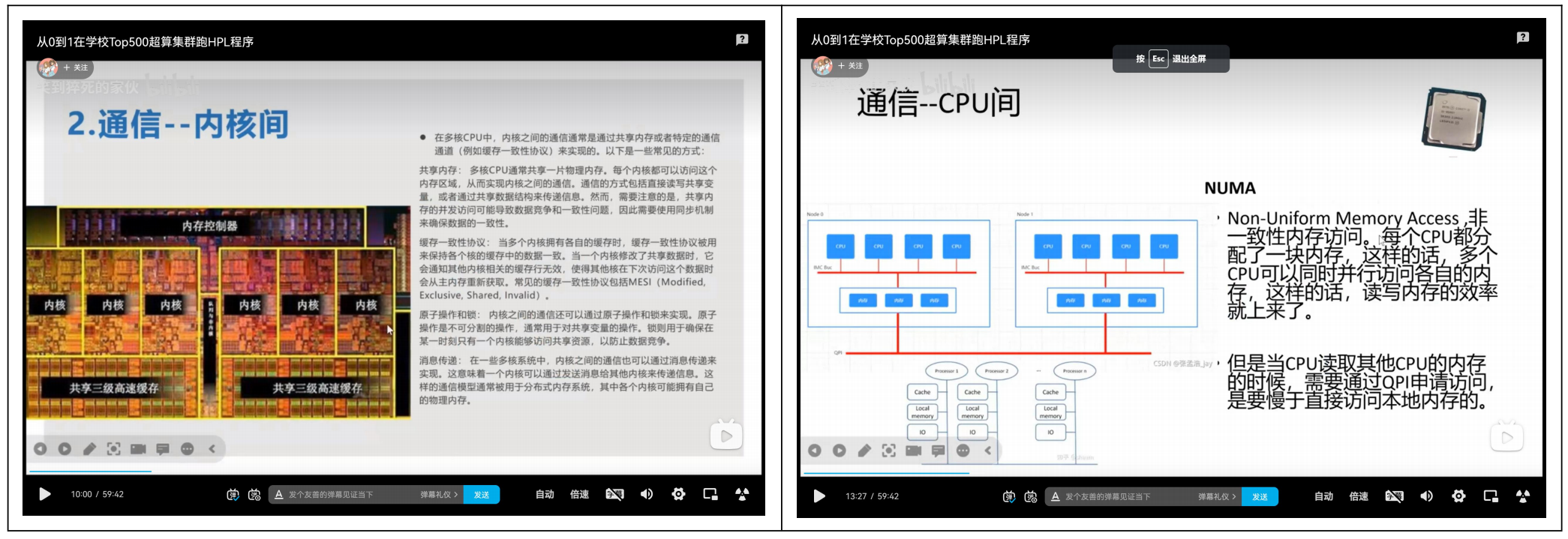
顺带一提,B站上有个UP视频讲这个讲的挺好的:

我们还有更重要的问题没有解决:为什么多线程程序的用时会随着问题规模的增大而增加的更多,从而变成一个 f'\left( x \right) >0,f''\left( x \right) <0 的函数呢?我推测还是通信的问题。
上学期教我数据库的老师告诉我,随着机器数量增加,计算性能并不能像是一条直线往上蹭蹭涨。当系统的通信开销大于我们的计算性能增长时,程序的执行效率就开始下降了。当然,更多的数据研究需要去做,留作给读者的练习。

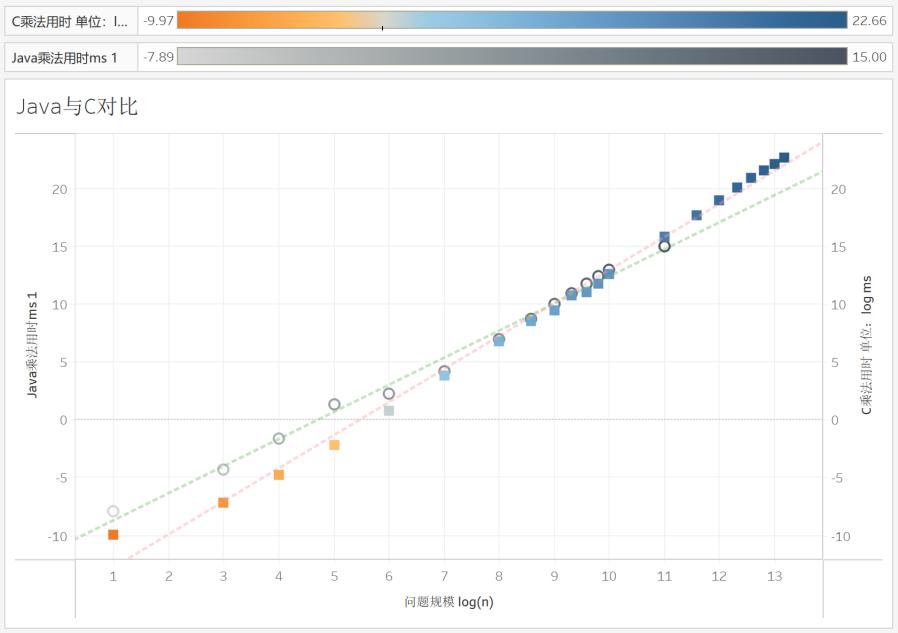
Java & C 矩阵乘法速度对比实验
我们继续来看一些有趣的事情,在试管1号Linux服务器上,Java乘法和C乘法的对比。开始C是占上风的,但是,如果按照我们的趋势线走,似乎Java将战胜C。诶?Java可以更强吗?
诶,但是我们看看试管2号的结果:C还是比Java强大!这是怎么回事?原来在不同的硬件平台,不同的操作系统上结果还能不一样的吗!
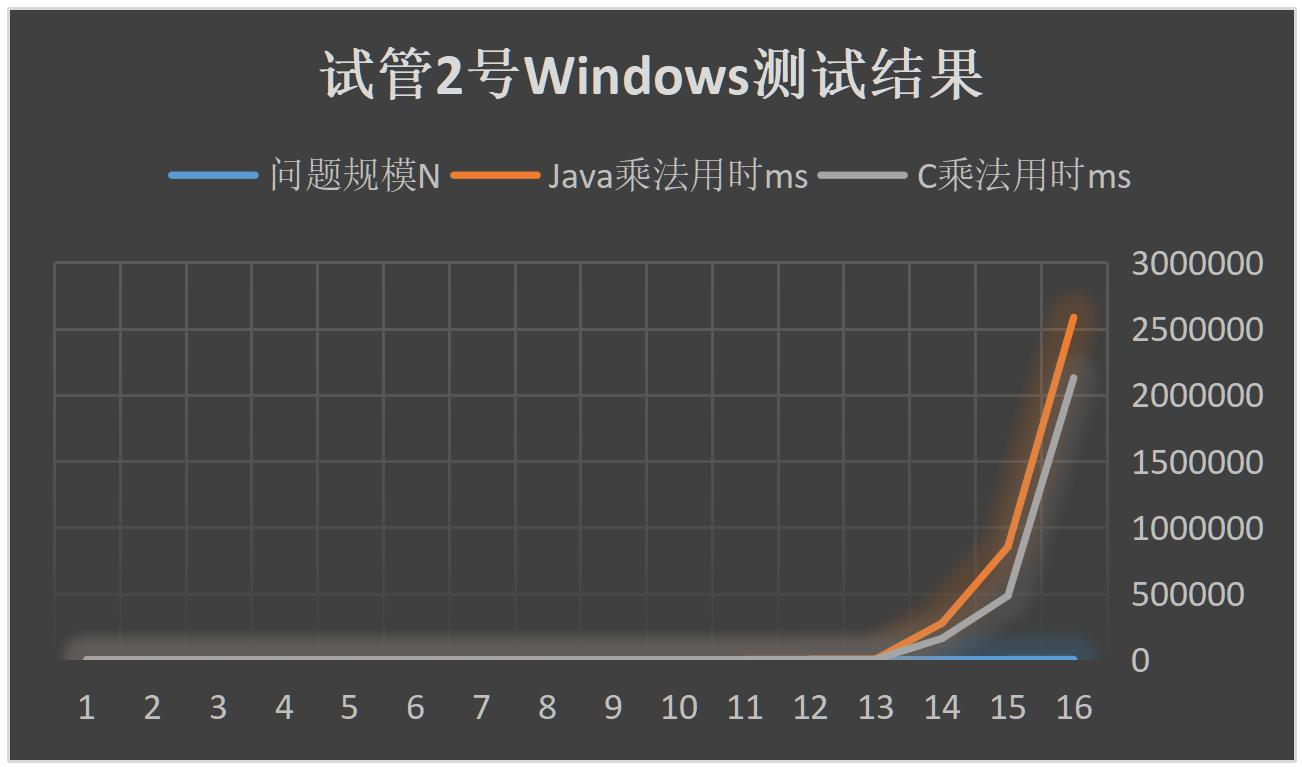
我认为这里的差异跟好几个因素有关:
-
硬件差异:试管1号是AMD CPU,试管2号是Intel CPU,他们执行着不同的指令集,面对不同的程序可能有不同的效果。
-
操作系统差异:Windows的dll库和Linux的动态库可能有差异,操作系统对程序的管理也可能导致程序在CPU运行的idle time,effect time有所不同。
-
环境差异:试管2号上安装了MinGW,Intel HPC Base Toolkit,VS,还有从2008年到2019年全部C++运行环境和400MB的dll补全库,以及最新版Intel MKL,而试管1号服务器上的C环境可能没有试管2号上那么“优秀”(玩太多游戏配的)。
-
编译器差异:两个试管的编译器不同,造成的优化可能也不同。
具体发生了哪个,还需要我们进一步探索,这里就给读者留作一道......
C OpenMP与O3优化速度实验
我们来看C自身的优化:OpenMP方面,前期OpenMP慢于普通C程序,推测是多线程开销所致。而后期在多核处理效果快于多线程开销后,OpenMP就比C程序快了。
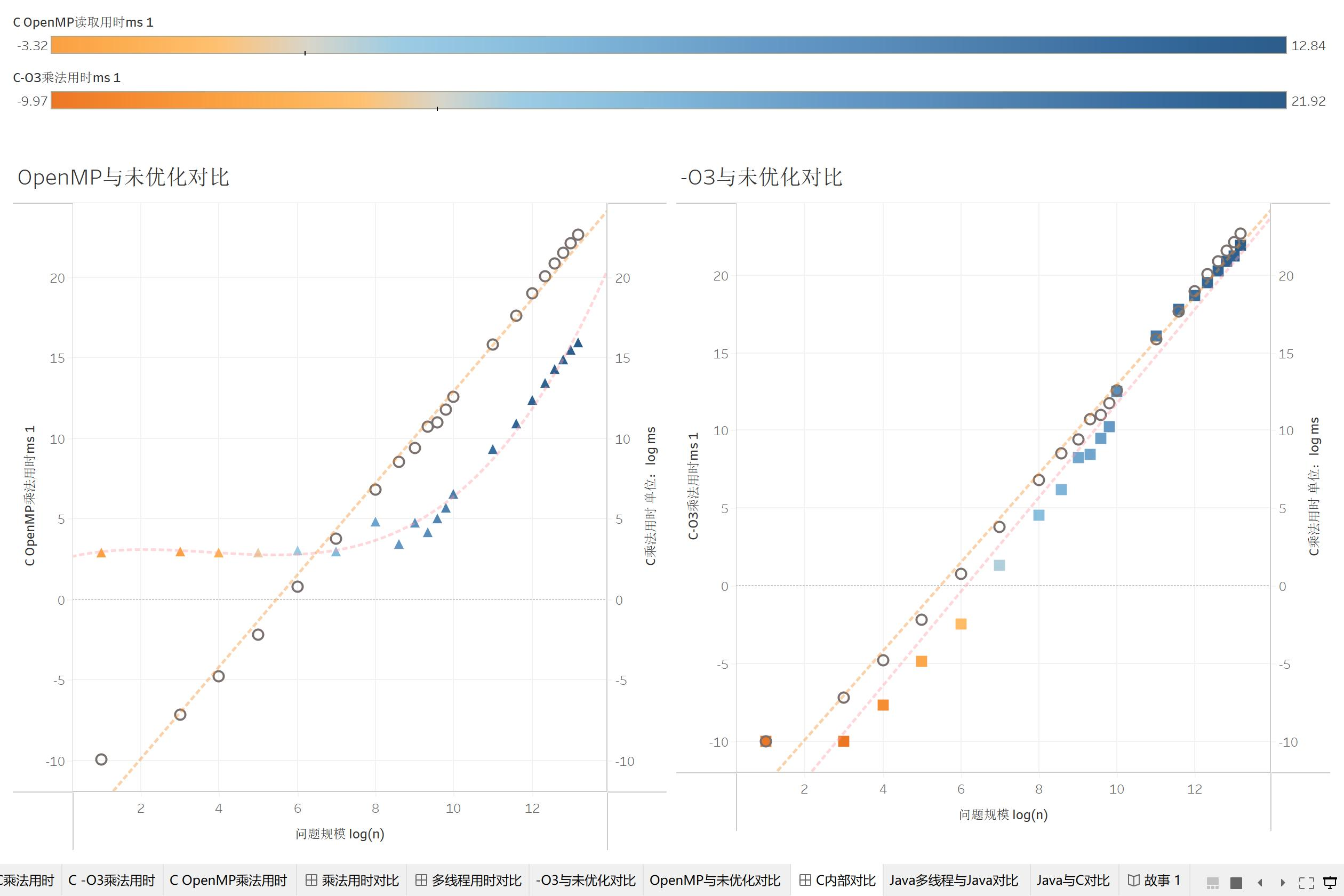
O3的也挺有意思的,一开始O3的执行速度带来的优化是比较明显的,但是随着问题规模指数的上涨,O3的优化逐渐缩小了。这并不代表O3废了,而是比如说一开始O3优化了二分之一,开了log很明显,但是后面优化在指数爆炸下就越来越不明显了。这说明O3的优化是类似于接近常数的优化,它将精简程序,但是这类编译器自动优化最终会随着数据规模的增加而显得疲软。因此,虽然O3可以很好地加速程序,但是随着数据量的增长,O3不能是一个程序的最终优化方案。
Java 多线程实验
最后我们来看看开了log处理的Java多线程和Java。这里我们就让Java最多开4个线程,相当于最多优化到4倍。可以观察到Java多线程的优化效果有点像OpenMP和O3的结合:前期因为创建线程导致速度不如正常Java,中期因为线程优化大于通信和创建线程,优化效果越来越大。然而多线程是类似于常数上的优化,所以像O3一样,多线程Java跟普通Java越来越接近,直到后面通信的成本让普通Java再次成功。
总结
这个实验其实很打破我的想象。首先,我们观测到了Java多线程和C OpenMP里通信对程序执行时间的影响。第二,平台和环境以及编译器不同,Java不一定就比C慢。接着,OpenMP和多线程的优化其实是有个区间的,多线程并不意味着就比单线程的快,我们的目标是要找到这个合理的区间。
5.4 运行时间 & 性能瓶颈实验结果
5.4.1运行时间实验结果
我们选取几个Profiler的结果对我们的程序进行分析。首先我们将分析Java。
我们根据以往我们的Java知识,Java程序在启动后,随即会启动一个JVM进程。JVM会导入字节码文件,这个过程叫类加载,把类放入到方法区中,并且启动程序计数器,JVM堆,JVM栈。随后JVM就像一个小CPU一样,读取指令,执行程序直到Main函数结束。
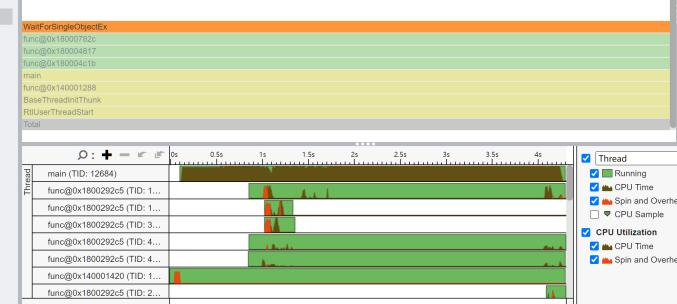
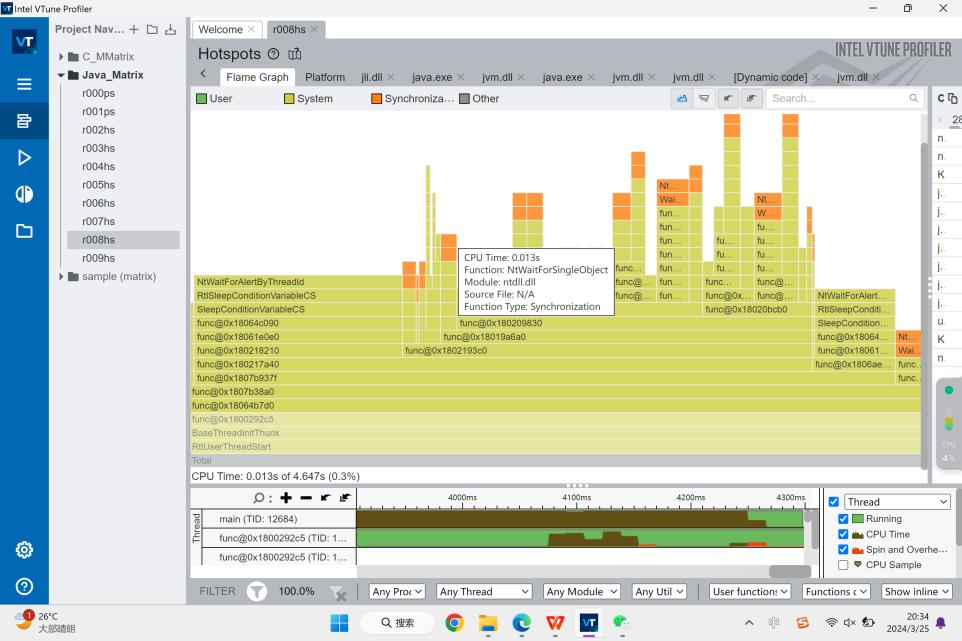
我们看看Profiler里程序的运行情况。发现程序在开始时,JVM并非是直接启动的。反而是WaitForSingleObjectEx函数先开始执行(橙色函数部分)。这似乎是操作系统层面同步的一个函数,我们根据微软的介绍,这个函数函数将检查指定对象的当前状态。https://learn.microsoft.com/zh-cn/windows/win32/api/synchapi/nf-synchapi-waitforsingleobject
并且此时,一个叫main的函数启动,初始化程序。我无法确认main是否就是Java里的main,因为此时JVM还没有启动,由此我推测,假如这个JVM是C写的,这可能是启动JVM的C语言Main函数。
接着是CreateJavaJVM。虽然它用时很长,但是它的汇编指令就那么短短几行。主要的花费在call这条指令上。这个方法我看不到具体的源码,但是根据Profiler里System的标注,我推测是唤起了系统层内的一个函数。
随后JVM开始了编译,具体到汇编层面可能就有点难看,对于每个方法,JVM会动态调用编译方法,将代码编译并存储到相应的地址,随后我们的Program Counter就可以一条一条地找到他们。

我们接下来看程序终止的时刻,这里有一堆程序在做事情,根据橙色的同步函数,我推测他们是JVM在终止自己的虚拟机部分,将不同的类进行终止。这个部分会占用300ms,所以其实和我们的时间占用并不大。
我们打开JVM的日志程序,看看JVM的内部启动了什么线程:
可以看到,JVM执行了我们的熟知的Main线程,连带着Compiler C1,C2,I/O池,GC垃圾回收器,导入的动态系统库,以及各种线程的操作记录。这说明刚刚我们的Vtune分析是正确的。
我们接下来看C的执行过程。可以看到,C执行的比较纯粹,但是我主要想看这个ntdll.dll是什么,它跟我们的程序有什么影响。

根据多方面的信息,ntdll.dll是重要的Windows NT内核级文件。描述了windows本地NTAPI的接口。我接着看到,像strcpy这样的函数都是存在ntdll.dll内的。看来它应该像是一个数学库一样的代码库,我们在执行程序时调用了它的api。那么在Linux里怎么办?我想可能还有别的对应的代码库。
但是Windows是怎么启动我们的C程序的?下面这个链接里的文章是这么提出的。
https://blog.csdn.net/cpp_mybest/article/details/80194158
当我们启动电脑进入桌面时,系统会创建 Explorer.exe 进程。Explorer.exe是Windows程序管理器 或者叫文件资源管理器,用于管理Windows图形壳,删除该程序会导致 Windows 图形界面无法使用。
当双击某个图标时,Explorer.exe进程的一个线程会侦测到这个操作,它根据注册表中的信息取得文件名,然后Explorer.exe 以这个文件名调用 CreateProcess 函数。注册表中有相关的项保存着双击操作的信息,如 exe 文件关联、启动 exe 的 Shell 是哪个。PC中的大多其它的进程都是 Explorer.exe 的子进程,因为它们都是由Explorer.exe 进程创建的。
接下来,我用一张图片大致总结了C程序的流程:Windows操作系统给程序创建进程线程,并将指针指向程序入口。
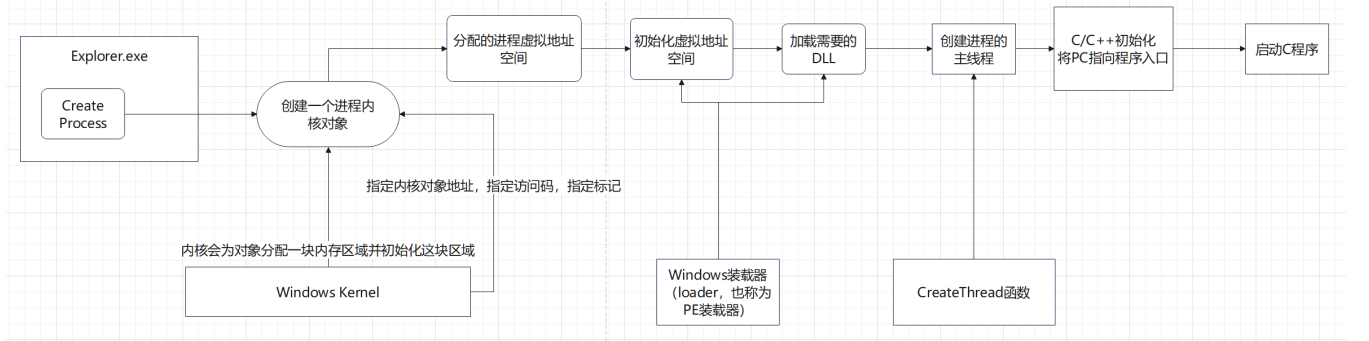
对于一个C程序,它在操作系统重将是一个进程块,有进程信息,线程,内存等资源。
那么,Linux操作系统会怎么做呢?下面这篇文章给出了他的实验结果:http://dbp-consulting.com/tutorials/debugging/linuxProgramStartup.html
在Linux中,每当我们回车输入./Matrix时,shell会让Linux调用execve函数,它将读取shell中的输入参数,把他们放到argc,argv中,然后Linux Kernel会给你像Windows一样配置进程,Loader会给你分配栈。
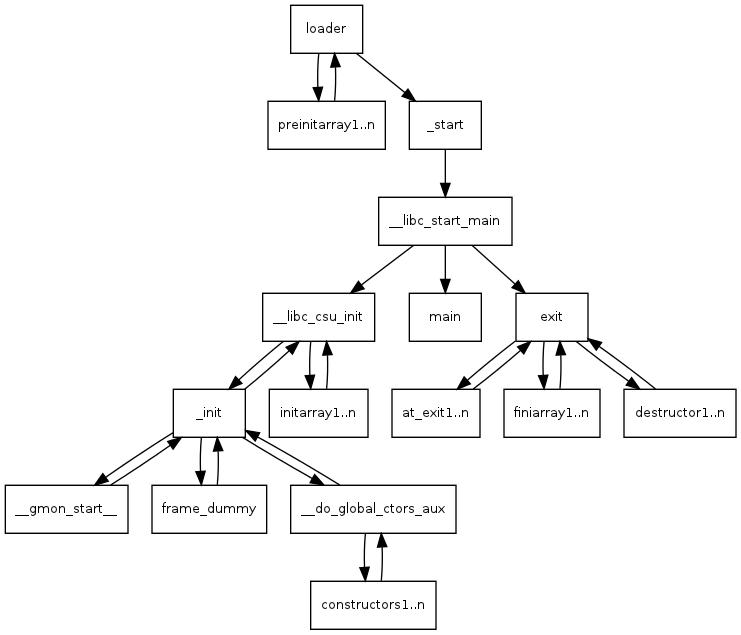

接下来,就来到了_start函数。根据汇编我们可以推测,_start函数会配置好eax,esp,edx以及栈指针,将我们的argv = %ecx等等。接下来,它将执行__libc_start_main。

libc_start_main 程序会在启动程序主线程,传入我们的argc和argv函数,调用glibc(GNU C Library),存储环境变量,根据指针地址启动Main函数。

到这里,我们的C程序就基本上进入到Main函数里了。
我们可以看到,在本次实验中,跟Java相比,C的执行更加地直接和迅速,所涉及的程序也是直接在操作系统层而非虚拟机层上。同时C的代码会被CPU直接执行,而Java代码会在编译中共同进行。
5.4.2程序瓶颈试分析
通过这几个实验,我们现在知道了我们C和Java程序的基本上全部的运行流程。那么,假如我想提高我们的程序的效率,我应该从哪些方面分析我们程序的瓶颈,让我们的程序加速呢?这里我们还是选择1000 * 1000的矩阵进行查看。
传统的分析方法是分析程序的CPU执行情况,分析我们的内存状况,分析IO。我们刚刚通过Profiler查看程序执行也基本上是服从这个传统分析方法。通过实验2我们知道,Java在执行程序上对字节码的优化还有所乏力,那么我们的Java程序瓶颈可能就在CPU方面。在C程序中我们的I/O读取判断逻辑似乎没有Java写的那么优秀,那么我们C程序的I/O读取逻辑可能就需要提升。而如果说我们的矩阵继续变大,大到我们的内存不够用时,矩阵增大将导致内存可能会变成新的瓶颈,操作系统很有可能会开启内存虚拟化技术,将我们的一部分矩阵存储在系统盘中,从而让我们的程序成功执行,并且使得我们的时间增加的系数增加。
对于矩阵范围增大导致的内存瓶颈,在软件上我们似乎没有太多能优化的地方,更直接的解决方案是换更快更宽更大的SSD,插上PCIe4.0。但是,像CPU方面的优化我们就可以动许多手脚。此时我们已经进入比较微观的视角,需要一套新的分析方案。
Top-Down Model
这里我找到了Ahmand Yasin的IEEE论文“A top-down method for performance analysis and counter architercture”。这是 Intel 公司提出的一套方法论叫 Top-Down 模型,它让每个CPU微指令对应不同的系统微资源的利用依赖度。他们建立了4种系统微资源的指令倾向类型,然后用4种类型去评估我们的CPU微指令。最终,我们汇总一个程序所有的微指令,让一个应用程序展现出4种不同的倾向性中的一种。使我们对程序在多核、高频、缓存上的使用有新的理解。
根据论文,这四种分别是:
-
Frontend bound(前端依赖) 首先需要注意的是这里的前端并不是指UI的前端,这里的前端指的是x86指令解码阶段的耗时。
-
Backend bound(后端依赖) 同样不同于其他“后端”的定义,这里指的是传统的CPU负责处理实际事务的能力。由于这一个部分相对其他部分来说,受程序指令的影响更为突出,这一块又划分出了两个分类。core bound(核心依赖)意味着系统将会更多的依赖于微指令的处理能力。memory bound(存储依赖)我这里不把memory翻译成内存的原因在于这里的memory包含了CPU L1~L3缓存的能力和传统的内存性能。
-
Bad speculation(错误的预测) 这一部分指的是由于CPU乱序执行预测错误导致额外的系统开销。
4. Retiring(拆卸) 字面理解是退休的意思,事实上这里指的是指令完成、等待指令切换,模块重新初始化的开销。
在这四种模型上,Intel工程师们将不同的Bound细分到各个模型中,比如分支预测错误归结到Bad speculation, Memory Bound归结到Backend Bound。具体见下图。
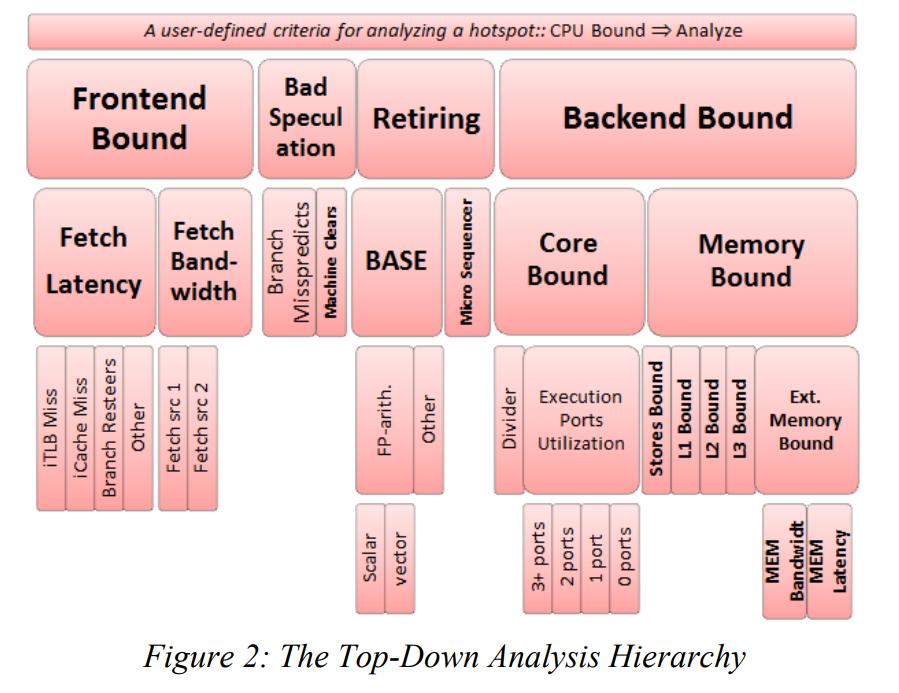
论文认为,我们在寻找程序的最大瓶颈时,可以像树搜索一样,先从4种程序瓶颈里找到最大的,然后再在这一种程序瓶颈里再找到问题最严重的,随后一步一步解决问题。比如在文章中,作者先给出4种瓶颈的判断方法,然后再细分查看各种瓶颈,比如Backend Bound里可能会有L1,L2,L3缓存的Bound,我们在确定分析Backend的情况下分析起来定位问题就会比较高效。
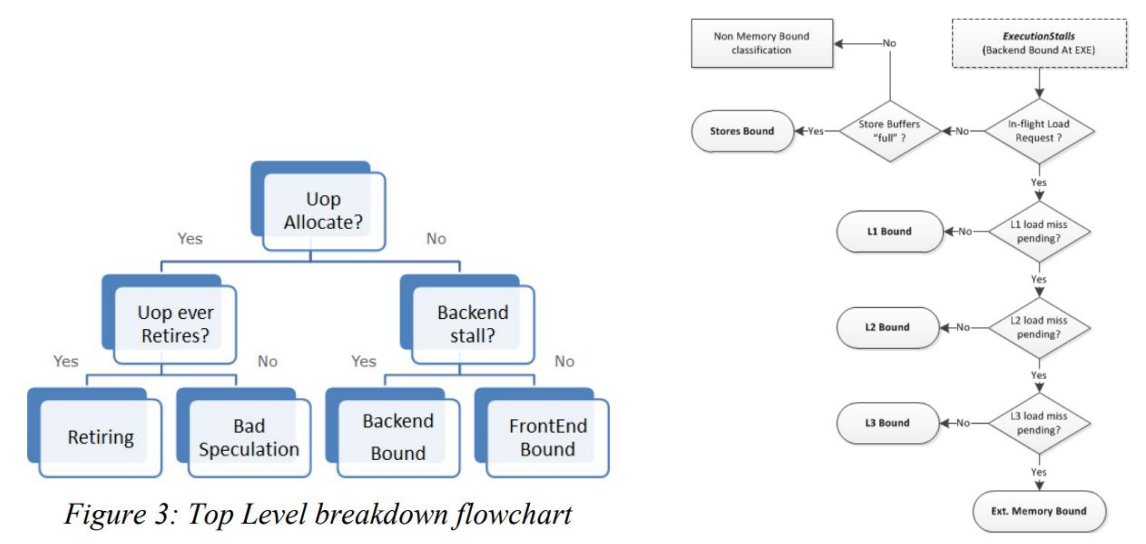
一位在英特尔中国的软件工程师[10]提出他们在Vtune上实现了这一模型。我随后在电脑上安装了完整的OneAPI HPC Toolkit查看我们的程序。
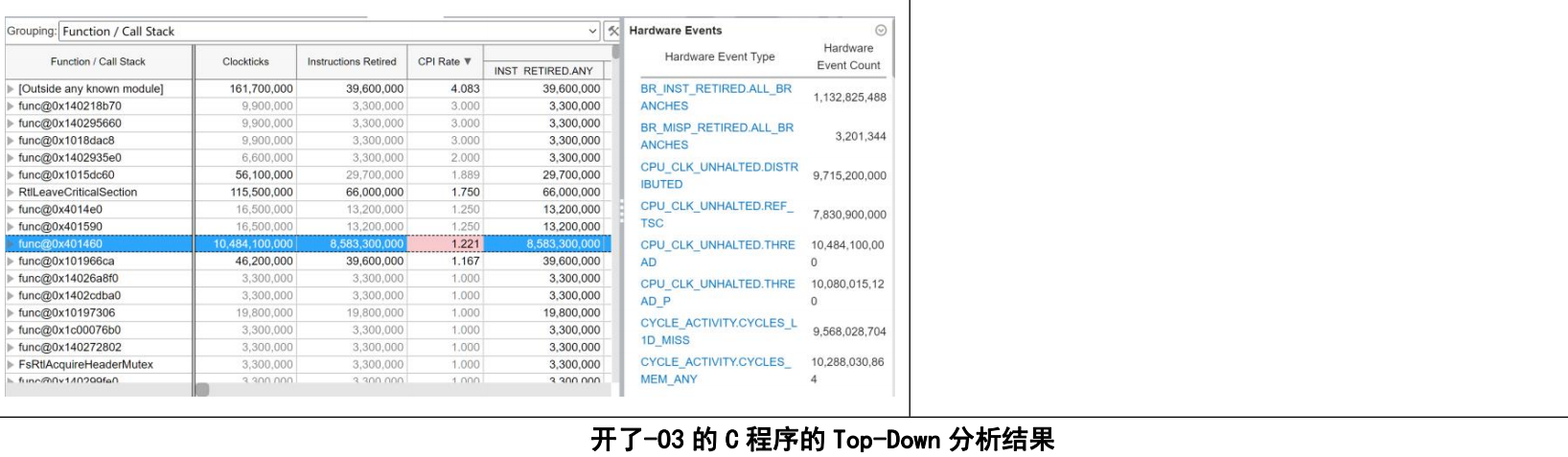
C 程序运行分析
我首先对我们的直接编译的C程序进行查看,Vtune返回了很多结果,从四种模型的Bound,程序的CPI,各种细分的Bound,不同函数的所用时钟数,指令数,CPI,CPU频率。
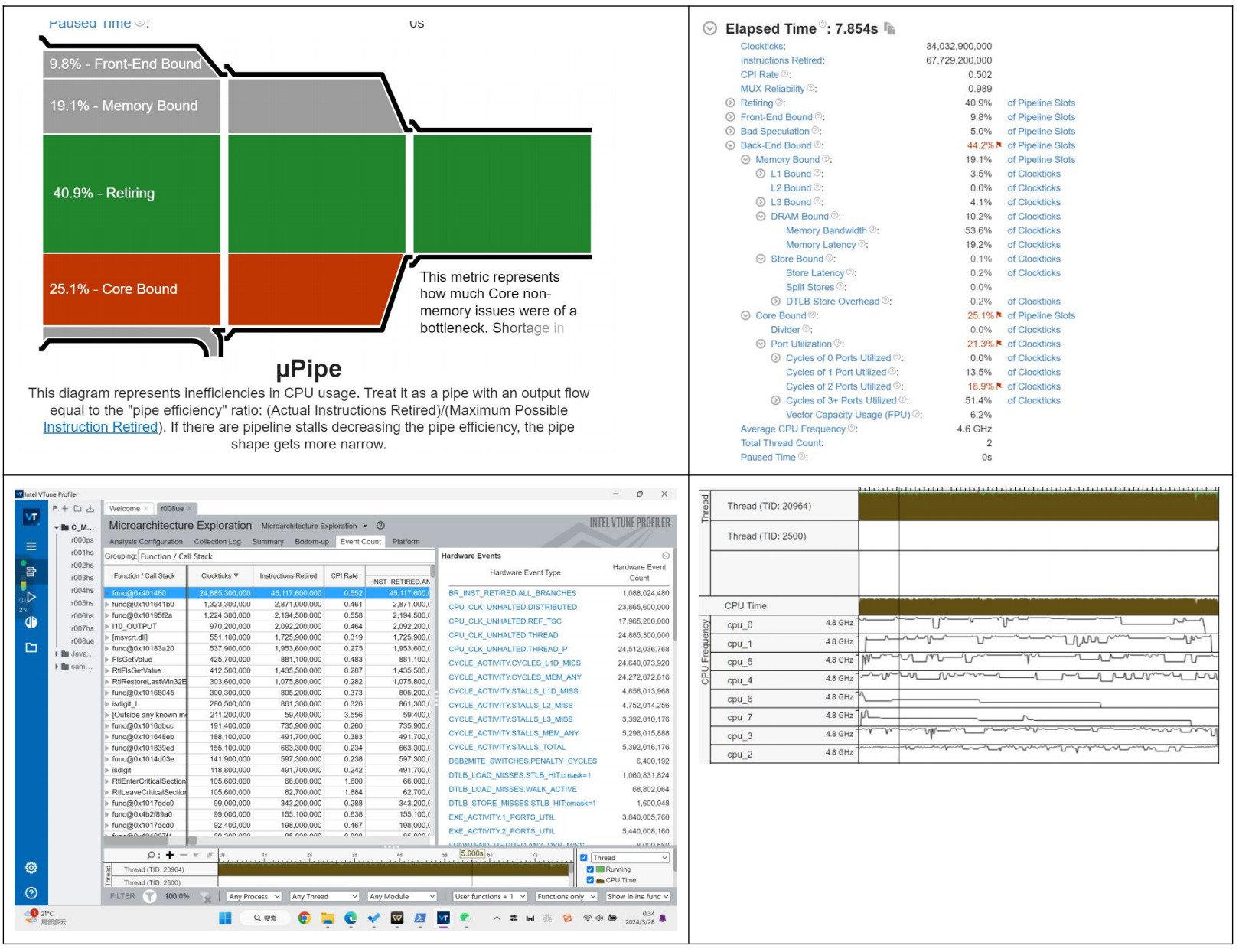
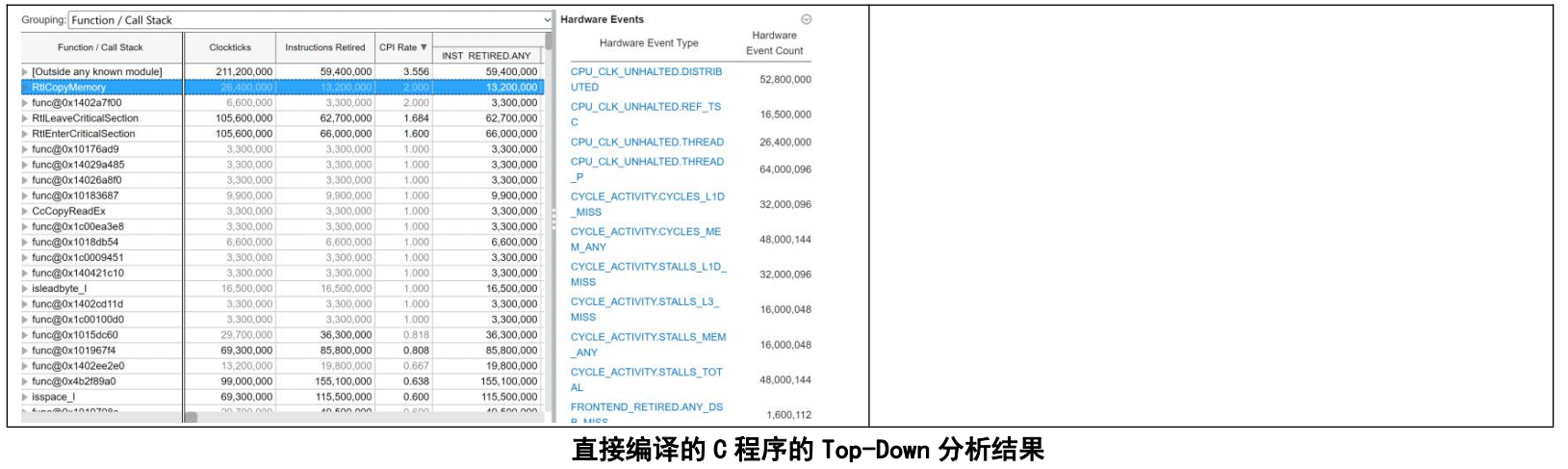
Profiler认为在程序中的最大瓶颈是 Core Bound(红色高亮),这属于Backend Bound。我们查看Backend里的性能瓶颈,比较严重的是Port Utilization,我们可以查看Profiler对这个的解释。它提出我们的端口之所以成为严重的瓶颈,很可能是相邻指令之间存在大量数据依赖性,或者一系列指令过度占用特定端口。接着它还提到一个提示提示:循环向量化 - 如今大多数编译器都具备自动向量化选项 - 可以减少对执行端口的压力,因为多个元素使用相同的uop进行计算。

回忆我们实验2所执行的直接编译的汇编代码,不难想到这部分描述的就是ijk三变量的瓶颈,他们由于存在内存中使得CPU花费很多的时间进行存储和读取。
从四种模型中我们也去查看Retiring的瓶颈,可以发现,程序在取址和内存操作上是比较严重的。他们的完成速度慢,从而拖累了指令的Retiring。根据实验2的汇编代码,我们可以推测因为大部分的取址是发生在ijk上,因而产生了这个瓶颈。

如果分析我们的具体各个函数,我们发现CPI最高的是copyMemory操作,这一点不难想象。而我们的主程序的CPI在0.552。主程序的瓶颈主要是Backend Bound,而这里边一个是Memory Bound的DRAM Bound。不难推测出,这是我们的矩阵存储的地方,CPU与DRAM的I/O自然会成为程序的重要瓶颈,如果我的电脑用了很多程序,使得Intel开启了内存虚拟化技术,我们的程序可能会跑得更慢。综上,I/O使得CPU的端口使用比较紧张。不过想到这里,我想到我的电脑CPU是UMA架构,如果对于服务器里的NUMA架构,CPU的Bound会不会增加呢?时间原因我没有测试。这个问题给读者留作练习(不是)。
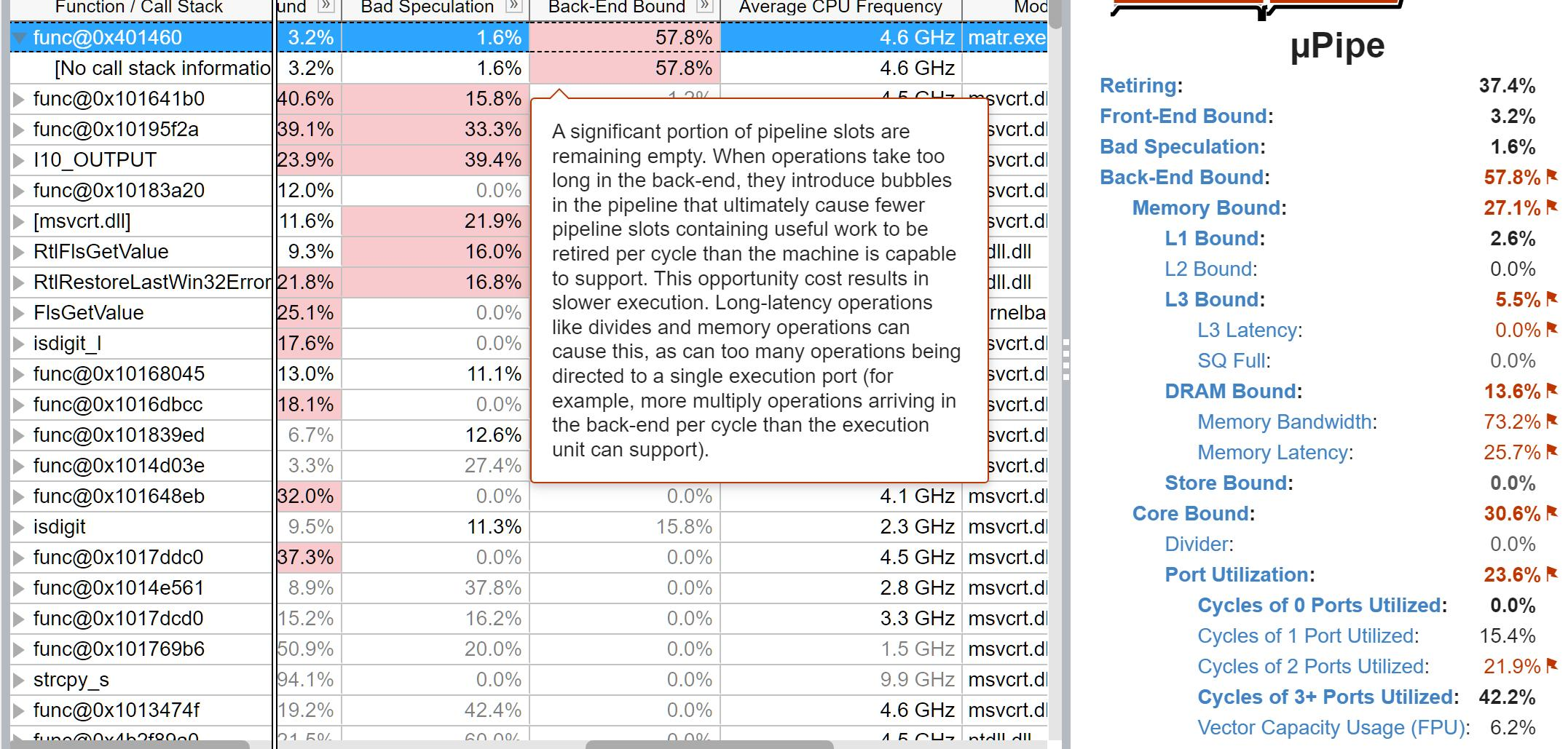
C -O3 程序运行分析
那我们接下来将测试-O3下的程序。
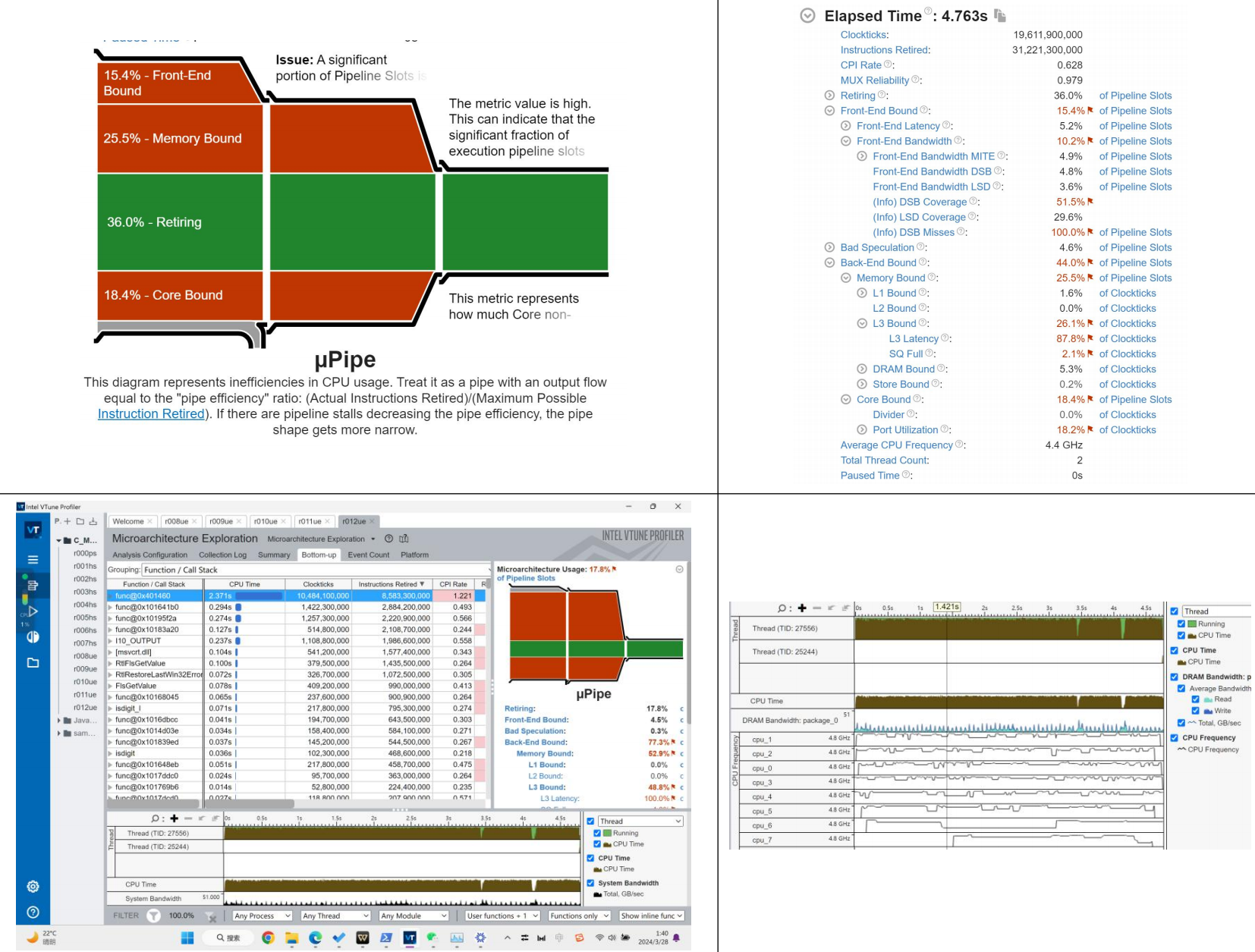
从-O3的结果上看,我们的程序在FrontEnd,MemoryBound,和BackEnd全成了瓶颈。这听起来可能不太妙,不过往另一个角度想,是不是因为优化的很厉害,所以才使得原本不是瓶颈的Bound变成瓶颈呢?
不过,这回MemoryBound里的具体瓶颈不再是DRAM的瓶颈,相反是L3 Cache的瓶颈。我认为这是编译器优化的结果。原本程序将数据存储在DRAM中,但是-O3会改变存储位置,尝试将数据导入到L3中。不过,这应该和我们的矩阵的问题规模有关,因为我们的L3大小只有12MB,如果继续增加N维数,DRAM可能还是会变成一个瓶颈。
FrontEnd的瓶颈似乎出现在各种Cache上。时间原因我就没有分析。
Backend的Core Bound里CPU的端口瓶颈下降了,从21.3%到18.4%。

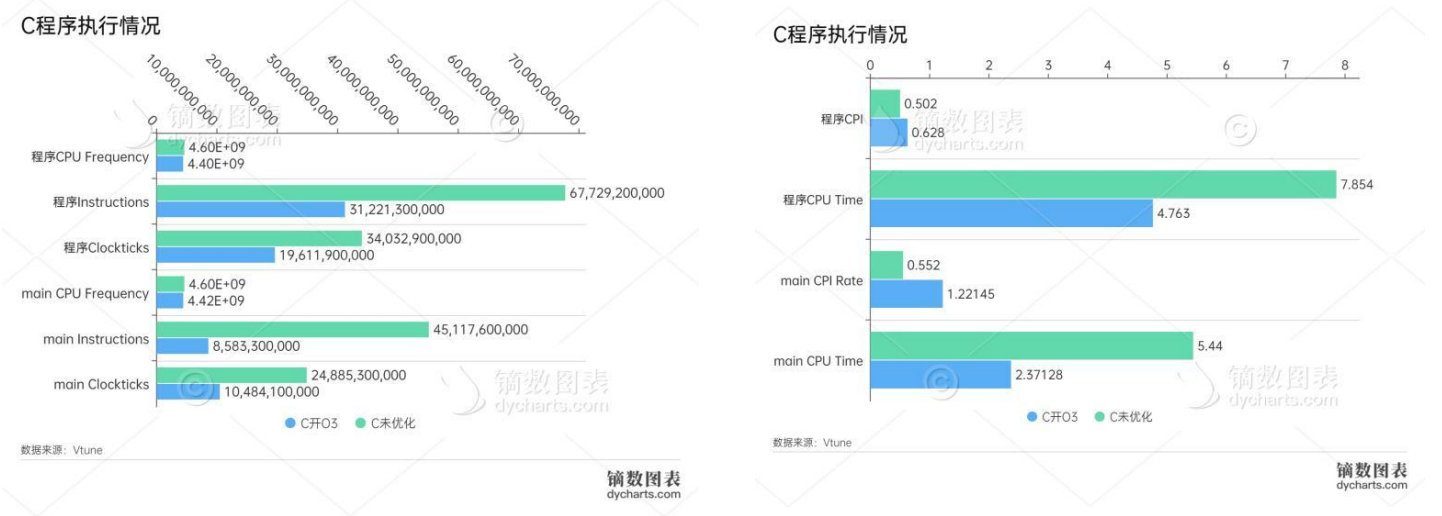
我们比较两个程序的执行情况。可以看到,使用了O3以后程序和main函数的CPI反而增加了,也就是说程序执行一条汇编代码所花的平均时间反而变长了,但是程序的总instructions几乎减少了一半,main函数的instruction几乎减少到原来的20%。这使得最后的CPU时钟花费在未优化的42%。
由此我们可以得出CPI增长的原因:程序的指令数大量减少,使得花费时间减少。但是减少的指令很多执行的速度是小于CPI的,比如我们在实验2中所看到的,在我们操作ijk的时候,我们用了很多add指令。这些指令花费的时间短,并且可以被优化。因而在开启编译器优化后,剩下来的指令所需要的平均时间增加,CPI也就增加了。这说明我在实验2的推测并不完全正确。其实从白老师做的实验也能看到,优化后的程序普遍CPI都发生了增长。
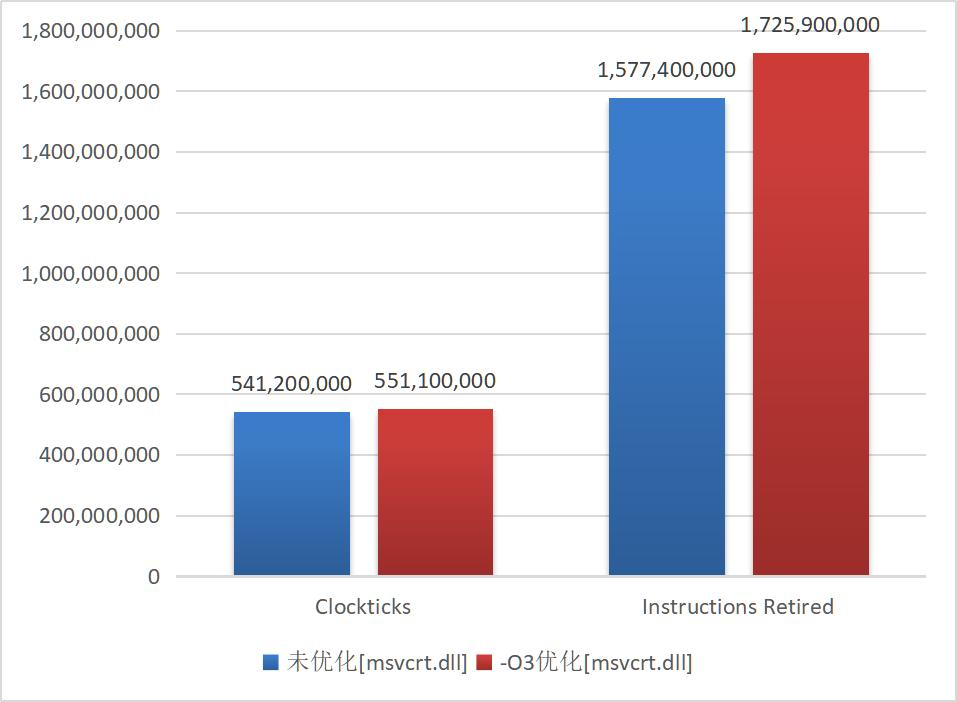
对比在dll库中使用的指令,-O3同样也进行了优化,程序用dll的汇编代码数也下降了。
Java 运行分析
接下来我们查看Java的运行情况。
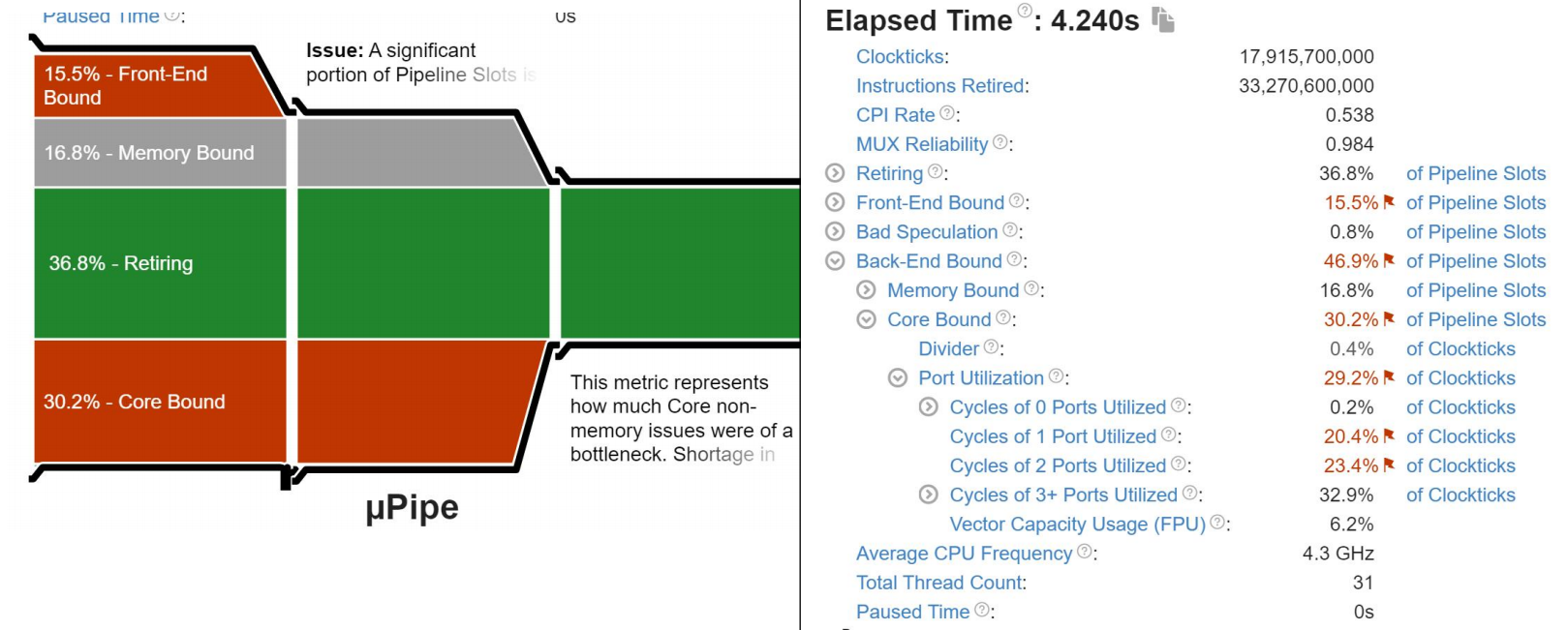
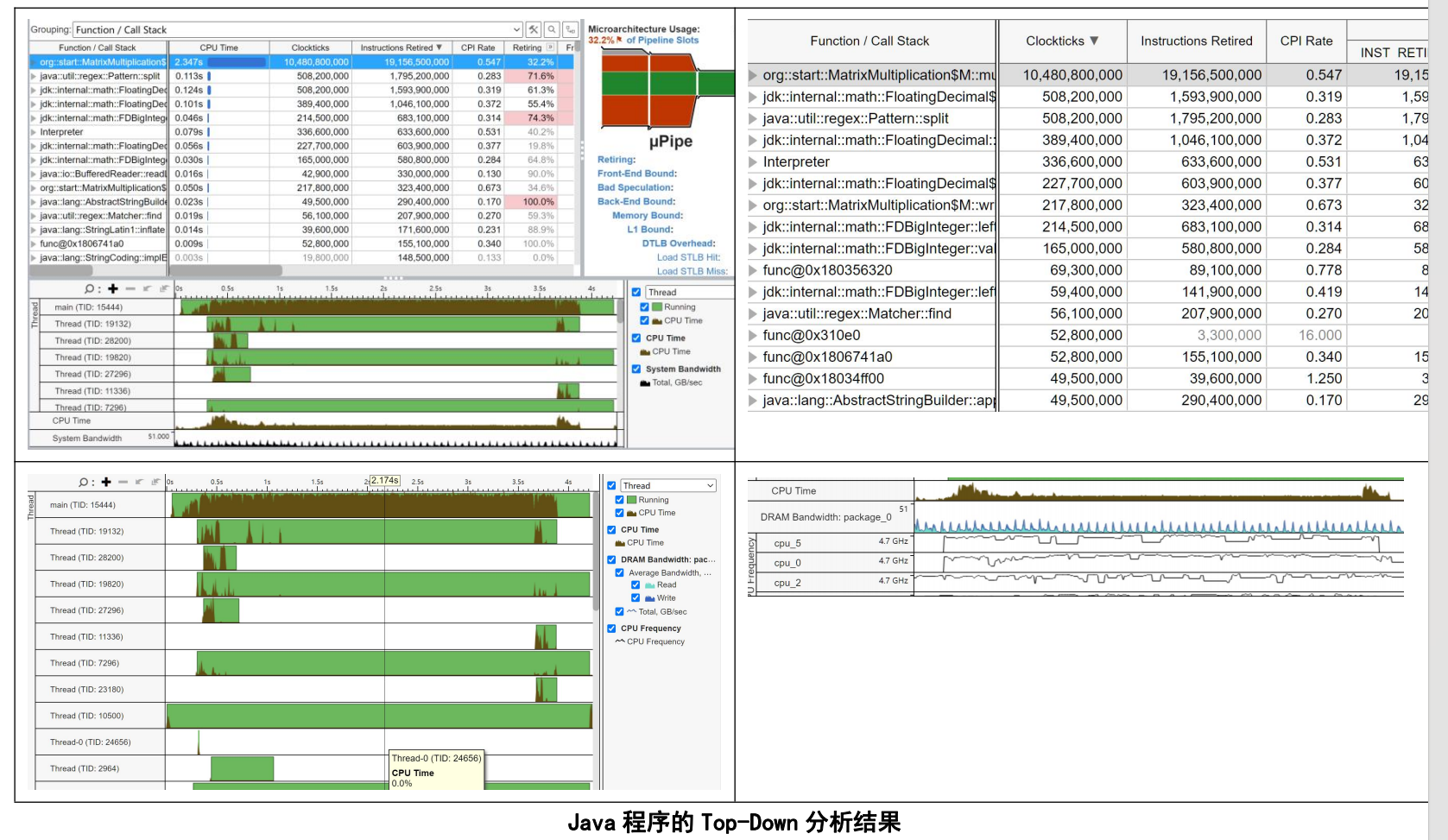
我们可以看到,Java的瓶颈会出现在Core上,并且还是CPU端口的问题,这个问题就跟他汇编代码一样,程序进行了很多次call,并将数据存储在DRAM中,因而出现了性能瓶颈。但是令人惊叹的是,Java程序在I/O上速度比C要好,以至于整个时间是比C程序快的,这可能是因为Java jdk内部的函数被优化的很好,并且比我写的C好。在矩阵乘法函数上Java的CPI似乎就比较低,和C未优化的效果是一样的。我们可以猜测这里Java的编译器就直接像C一样翻译代码,从而效果就比较普通。
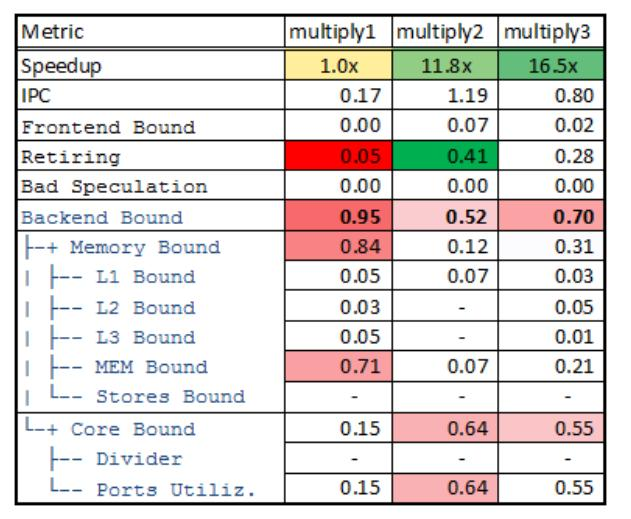
值得一提的是,Intel官方也拿矩阵乘法做了测试,对不同的矩阵算法进行了分析,我们也可以对比他们的结果看看。
小结
所以综上我们看到,未优化的C程序在端口取地址上存在瓶颈,同时未优化程序的汇编指令多,执行的速度就比较慢。而开了O3的C程序将DRAM存储主要改为了L3存储和寄存器存储,性能有了许多优化,但是可能在I/O方面函数写的比较朴素,函数依旧花费了比较多的时间。Java程序和未优化的C程序类似,主要的瓶颈也是在汇编指令数和端口地址上,对汇编和地址的优化没有C编译器那么强大。
Part 6: 实验背后的理论
6.1 矩阵乘法的发展
这部分来源于我自己对各个文章的整理,可以作为我们的研究综述开头。
矩阵乘法是一门近代研究方向。1812年,Binet和Cauchy发现了最初了行列式乘法。1858年,Cayley在他们的基础上,研究出了我们今天线性代数课上所讲的矩阵乘法:result[i][j] += matrix1[i][k] * matrix2[k][j]; 如果你的研究方向不是理论计算机科学或者计算数学,这些知识足够应对现实的各种问题。

随着计算机科学的发展,人们开始思考,能不能从最基础的乘法层面进行加速?
1969年,Volker Strassen发表文章提出一种渐进快于平凡算法的n x n矩阵相乘算法(n为2的幂次方),引起巨大轰动。在此之前,很少人想过能快于平凡算法的方法。矩阵乘法的渐近上界自此被改进了。
矩阵乘法提升速度的关键在于减少乘法步骤的数量,尽可能将指数从 3(传统方法)降低。可能的最低值 n²,就是写出答案所需的时间。计算机科学家把这个指数称为 Ω,或者 ω。nω 是当 n 越来越大时,成功将两个 n×n 矩阵相乘所需的最少步骤。
Strassen算法的大致想法是,我们的传统做法是将大矩阵之间用最朴素地ijk三循环进行相乘。那么对于2x2的矩阵相乘,一共需要23即8次乘法运算。但是Strassen天才地发现,2 x 2的小矩阵之间的计算可以只用7次乘法运算,随后 Shmuel Winograd证明,我们找不到低于7次的运算方法。

1986 年,Strassen 取得了另一项重大突破,他推出了矩阵乘法的激光法。Strassen 用它确定了 ω 的上限值为 2.48。虽然该方法只是大型矩阵乘法的一个步骤,但却是最重要的步骤之一,计算机科学家一直在不断改进它。
激光法的大致工作原理是,将重叠的块标记为垃圾,并安排处理,而其他块被认为有价值并将被保存。
在做Project的这些天,刚好有一个新闻发了出来:清华姚班本科生连发两作,十年来最大改进:矩阵乘法接近理论最优
姚班学长的文章提出,Strassen算法里有一些“hidden loss”。他们是激光法中被程序抛弃的矩阵块,而这些被标记为垃圾的块被发现还是有利用效率的。于是他们修改了激光法的标记方法,将理论复杂度下降到n的2.371552次方,较之前的方法低了0.0001,但已经是这10年最强的进步。
不过,学长并没有在代码层面实现算法。不难理解,这些方法的常数已经让复杂度的降低变得很鸡肋,且算法的长度也杜绝了大部分程序员的尝试。但是,这些突破不断启发我们,哪怕是再寻常,再基础的计算,或许也有更快,更强的方法出现。
6.2 Strassen 矩阵算法详解
这里的原理主要源于https://zhuanlan.zhihu.com/p/268392799。当然,我后来又看了《算法导论》,发现神书已经详细讲解了这个算法,并且还进行了多线程的实现。在读完整个过程后,我跪倒在地,不愧是神书!
首先我们会先将A,B两个大矩阵分成4个小矩阵,用时为O(1) 。我们用C表示A x B的结果:
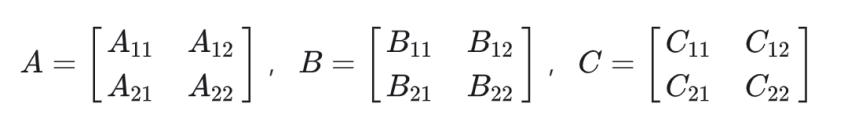
紧接着,计算10个小矩阵之间的加减,存为S花费时间为 O(n^2)。

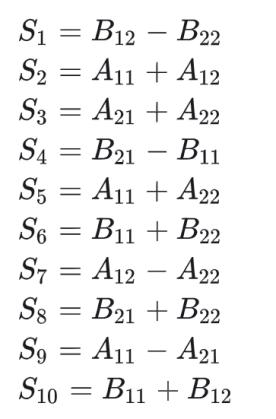
随后计算7次矩阵乘法,得到7个P矩阵:
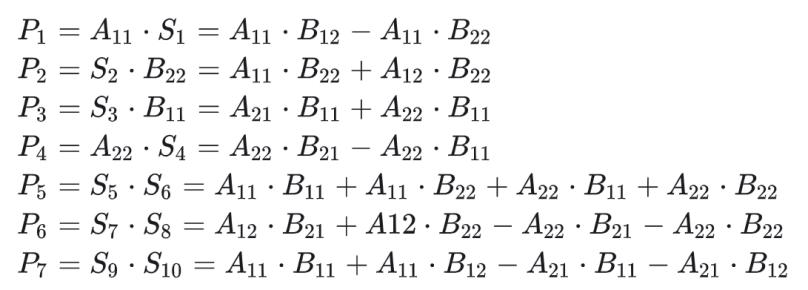
之后我们就可以得到C矩阵:
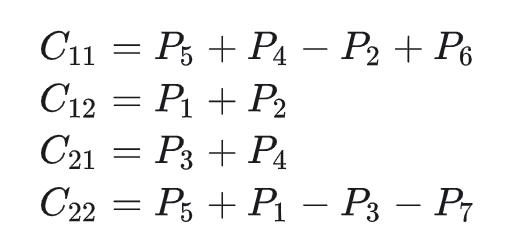
这样我们就计算出A x B的值了。通过上面的计算过程,我们得到算法的时间递归式:
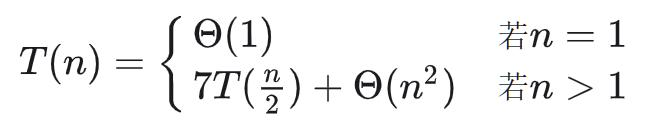
进而我们就可以得到我们的算法时间复杂度:
T\left( n \right) =\varTheta \left( n^{\log 7} \right)
我们把n的三次方和 log7 画图,还是能明显看到两者的区别。
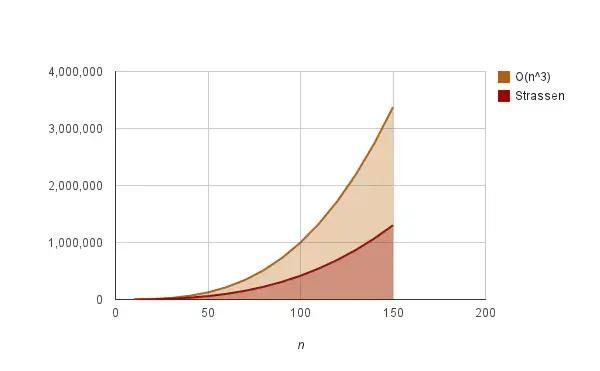
可以看出,Strassen算法确实在一定程度上降低了时间复杂度和运算时间,但是,每次矩阵运算都需要大量的内存用于临时存储P和S矩阵,当问题规模N很大时是非常致命的,这导致同样的集群我们可能算不了更大的矩阵。同时Strassen算法增加了多步加法来换取乘法步骤的减少,这让算法的常数增加,在运用中实际使得算法要在N大到一定程度时才有优势。可是综合来看,在算法有优势时集群没优势,会让这个算法的地位变得有点尴尬。但是,它确实对矩阵计算进行了加速,对于今天的图像处理等操作有着非常重要的意义。
6.3 Intel Top-down性能分析模型 乘法分析
初始代码 multiply1() 极为内存受限,因为它以不利于缓存的方式遍历大型矩阵。在 multiply2() 中应用的循环交换优化大大提高了速度。尽管如此,经过优化的代码仍然是后端受限,但现在它从内存受限转变为核心受限。接下来,在 multiply3() 中尝试了向量化,因为它减少了端口利用率,减少了净指令数,从而实现了另一个加速。
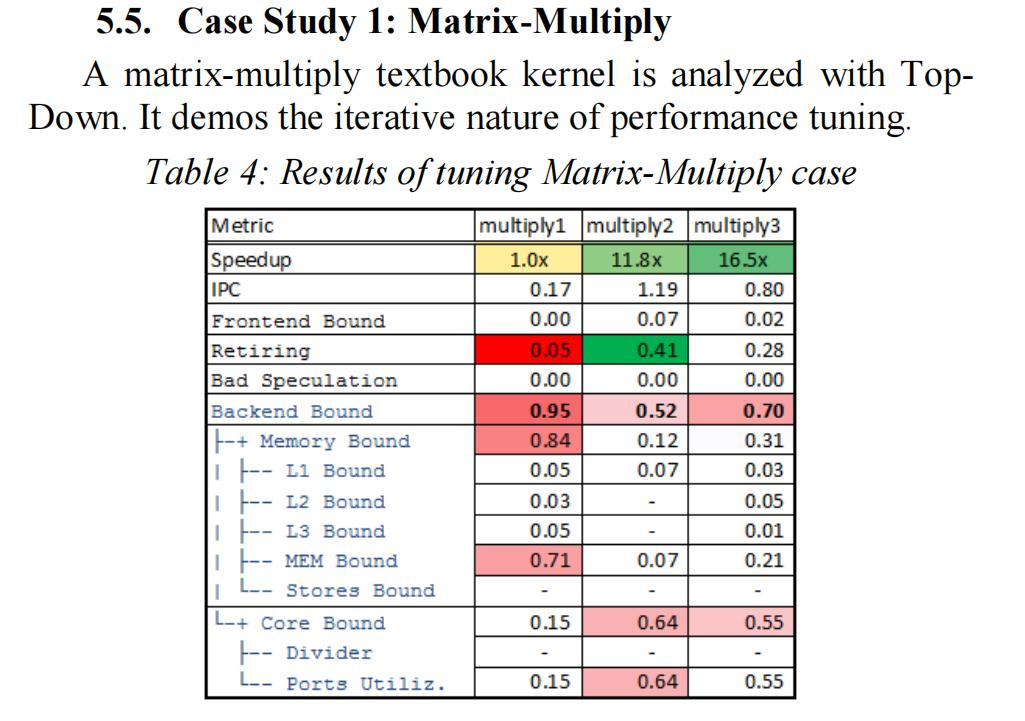
下面是英特尔工程师的分析:

Part 7: More Jobs can be done
1.对于实验1,Java内部代码是如何实现精度的估算的?
2.对于实验2,Java内部各个代码是如何实现的?由于通信的影响,我们的多线程函数什么时候是弊大于利的?
3.对于实验3,能不能换一个更有代表性的矩阵读取和写入函数?不同程序唤起的时间记录函数不同,有没有什么好方法能让程序同时用同一个函数记录时间?
4.对于实验4,让程序CPI上涨的函数为什么要花更多的时钟周期?为什么有的指令就不用那么多时钟周期?CPI在我们这次的测试里是越高越好还是越低越好?
5.GPU版本的测试与探索。GPU里的代码如何执行?
6.随着N的增加,Cache,DRAM,乃至虚拟化的内存会不会成为新的瓶颈?UMA和NUMA跨节点影响我们的程序运行时间的效果怎么样?OpenMP多核时的程序运行时间是否和核的布置有关?
6.所有给读者留作的练习。
Java真的跑的比C慢吗?我们可以看到其实刚刚在多核情况下,Java是可以多线程启动的,而这相比于单线程C程序会有一定弥补。如果在C没优化的状态下,他们之间的差距会更加缩小,可能最后,程序执行我们平时交了这么多次OJ,大家都喜欢C++,但是在真实情况下Java带来的性能牺牲没有我们想象的那么大?
Part 8: 总结
我们在本次Project中共进行了4次实验,分别对C和Java在矩阵乘法程序中的精度、编译效率、运行时间和启动方法进行了观测。
通过实验,我们发现了几个关键的性能差异点:
-
精度判定:Java在执行时会自动判定float精度,而C语言不会,这可能对性能产生一定影响。
-
JVM和编译器的影响:Java的性能受到JVM和JIT编译器的影响。JIT的C1C2编译器效果不明显,而C语言使用-O3编译优化可以将变量优化到寄存器中,减少汇编指令和内存读取指令,从而降低运行时间。
-
平台差异:在不同的软硬件环境和编译器下,Java和C的表现有所差异,这意味着性能也可能受到具体实施环境的影响。
-
多线程和通信瓶颈:Java的多线程和C的OpenMP在通信上可能存在瓶颈,多线程不一定比单线程性能更优。
-
启动方式和操作系统的影响:Java和C的不同启动方式以及Linux和Windows的调用程序方式可能影响程序的性能。
-
性能分析法的应用:通过使用Intel TopDown性能分析法,我们能分析Java和C程序的运行瓶颈,以及CPI变化的原因。
综合来看,通过一系列实验,我认为Java和C在矩阵乘法操作中的性能差异多受编译器优化、运行时环境、编程语言特性以及操作系统等因素的影响。在不同的实现细节和优化水平下,两者的性能表现可能会有很大差异,因此不能简单地断言哪种语言绝对更快。
ChatGLM补充到:我们在选择技术栈时,需要考虑具体的应用场景、性能需求和开发维护的复杂度等因素。
我认为比较开心的一点是,这次Project我学到了很多性能分析操作,想明白了很多没想过的问题,实验都是自己设计自己完成,并且找到了自己想证明的知识,并且还跑通了Intel工程师跑通的实验。我对自己在以后优化程序上更加有信心,并且对整个优化要走的流程有了更系统的经验。我感受到一种探索的乐趣,这也一直让我坚信我确实应该要尝试做做科研。
我在跑时间测试的时候去读了海子的诗
突然觉得 诗歌就是一段段汇编语言
指针跳转,语句走了一行又一行
内存翻了一页又一页
我突然想到
等程序跑完,我会躺在哪片麦地上呢
风扇呼呼 就像海子笔下麦子谦卑的呢喃
终于,我看到
目击众神死亡的草原上野花一片
于是,我写下
远在内存的指针比内存更远
Part 9: Acknowledgement
感谢肖翊成同学和邱俊杰同学在“试管1号”装机和配置系统上的帮助,从底层配置BIOS,IB,学习BMC等等让我受益良多。感谢超算中心的硬件提供和网络支持。感谢马国恒同学,在我Project生病时帮我带饭和录了lab老师的讲解,我很荣幸拥有这样的舍友。感谢白雨卉老师在编译器优化上的实验和在计组课上给我的答疑。
Reference
[1] StrassenMultiplier.java A program that implement Strassen Algorithm: by JinGe Wang. Retrieved from Algorithms/src/matrix/StrassenMultiplier.java at master · jingedawang/Algorithms (github.com)
[2] Duan, R., Wu, H., & Zhou, R. (2022). Faster Matrix Multiplication via Asymmetric Hashing. 2023 IEEE 64th Annual Symposium on Foundations of Computer Science (FOCS), 2129-2138.
[3] New Breakthrough Brings Matrix Multiplication Closer to Ideal New Breakthrough Brings Matrix Multiplication Closer to Ideal | Quanta Magazine
[4] History of Matrix Multiplication When was Matrix Multiplication invented? (harvard.edu)
[5] 南方科技大学2023Fall数据库(H)Project1 DBMS赖海斌.pdf (sustech.edu.cn)(哈哈,怎么还王婆卖瓜引用起自己来了)
[6] WaitForSingleObjectEx方法解释_https://learn.microsoft.com/zh-cn/windows/win32/api/synchapi/nf-synchapi-waitforsingleobject
[8] Gunther, N. J. (2008). A General Theory of Computational Scalability Based on Rational Functions. arXiv, https://doi.org/10.48550/arXiv.0808.1431
[9] Yasin, A. (2014, March). A top-down method for performance analysis and counters architecture. In 2014 IEEE International Symposium on Performance Analysis of Systems and Software (ISPASS) (pp. 35-44). IEEE. https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=6844459
[10] Top-down性能分析模型 https://zhuanlan.zhihu.com/p/34688930
[11] 从0到1在学校Top500超算集群跑HPL程序_哔哩哔哩_bilibili
