CPP Project1 A “Simple” Calculator
- CPP
- 2024-08-27
- 2012 Views
- 1 Comments
CS205 · C/C++ Programming
Project1 Report: A "Simple" Calculator
PDF 版本:Project1赖海斌
Github: https://github.com/HaibinLai/CS205-CPP-Programing-Project
摘要
在本次 Project 中,我初步用C 实现了一个简单的计算器,可以简单地完成项目需求。 在计算器的输入有效数字小于 8 位时,我阅读了 IEEE 754 标准,使用 double 的加减法进行 运算。在计算器输入数字大于 8 位时,我借鉴了 Postgresql 数据库中 numeric 的实现方法, 使用数组进行精确计算。我注意到内存泄露的问题,并构建了一个内存控制检测系统,可以 减少我的内存泄露。另外,我学习了解了 OpenMP 与 CUDA 编程上,各自写了一个乘法方 法,可惜由于身体原因没能测试性能。除此之外,我了解了大整数乘法等计算器在现代的应 用,比如在密码学中的加密,科学计算等。我也了解了算法,比如 Karatsuba 乘法算法。
关键词:IEEE754 Standard; Postgresql Source Code; Memory Leak; OpenMP; CUDA;
Contents

Part 1: 需求分析
基本需求: 处理输入字符串,加减乘除,大数运算和指数运算。初看会觉得很简单,
但是其实里边涵盖了 C 中的字符,数据类型的了解,要应用条件与分支语句,初步探索
指针和 C 特有的内存泄露。除此之外,还有一些算法设计。
本质: 了解 C 的基本语法,C 中对字符串及各种数据类型的处理,学习 C 指针,学习用
C 写简单的算法。了解精确计算、科学计算以及大整数乘法的应用,要求我
去了解数值计算领域。
Part 2: 环境配置/编译
硬件使用南科大科学与工程计算中心的计算工作站一台,拥有 2CPU 128 核,总内存约
为 500GB。工作站共装配三台 NVIDIA A100 GPU。详见表 2.1,表 2.2。
| CPU Architecture | x86_64 |
|---|---|
| Model name | AMD EPYC 7773X 64-Core Processor |
| CPU family | 25 |
| Thread(s) per core | 1 |
| CPU(s) | 128 |
| Core(s) per socket | 64 |
| CPU max MHz | 3527.7339 |
| CPU min MHz | 1500.0000 |
表2.1 硬件CPU环境
| GPU name | A100-SXM4-80GB |
|---|---|
| GPU amount | 3 |
| CUDA Version | 12.4 |
| Driver Version | 550.54.14 |
| Memory | 98304MiB |
表2.2 硬件GPU环境
服务器内操作系统为最新版Ubuntu 23.04,gcc编译器版本为12.3.0,CUDA版本为12.4,CUDA编译器nvcc版本11.8。详细软件配置见表2.3。
| Software | Version |
|---|---|
| Operating System | Ubuntu 23.04 |
| OS Kernel | Linux H3C1 6.2.0-39-generic |
| gcc | (Ubuntu 12.3.0-1ubuntu1~23.04) 12.3.0 |
| nvcc: NVIDIA (R) Cuda compiler driver | release 11.8, V11.8.89 |
| Vim | Vi IMproved 9.0 (2022 Jun 28) |
| VScode Server | 1.87.1 |
| Math Library | ISO C99 |
| btop | V1.2.13 |
| nvitop | 1.3.2 |
表2.3 软件环境
本次Project使用了以下几个C语言库,下表2.4展示了他们的版本和用途。
| Library | Version | Usage |
|---|---|---|
| stdio.h | 跟随gcc | 使用标准输入输出函数 |
| stdlib.h | 跟随gcc | 使用malloc,free函数 |
| string.h | 跟随gcc | 判断字符串长度,比较 |
| unistd.h | 跟随gcc | 打开本地txt文件进行计算 |
| math.h | 跟随gcc | -lm调用本地C99数学库。仅作为计算器拓展功能使用,本次Project没有详细使用该功能 |
| omp.h | 跟随gcc | 使用OpenMP实现乘法的并行计算 |
| gmp.h | 6.3.0 | 快速计算大整数乘法库。作为与我写的乘法库的比较,也可作为计算器的辅助功能。 |
| sodium.h | 1.0.18 | 一个大数计算、随机数生成及多种加解密算法生成库。仅作为学习大数乘除法在密码学中的应用,对计算器没有过多作用。 |
| pbc.h | 0.5.14 | 基于GMP数学库的密码学库,在本次Project中仅作为全同态加密方面的了解学习而使用,对计算器没有过多作用。 |
表2.4 相关库配置
这几个额外安装的库只是作为学习使用,当然也可以作为计算器的一个插件。具体安装都比较简单:
在Linux中安装GMP库可以使用如下命令(测试计算器性能用,可有可无):
wget https://gmplib.org/download/gmp/gmp-6.3.0.tar.xz
tar -xvzf gmp-6.3.0.tar.xz
cd gmp-6.3.0
./configure
make # 编译
make check # 检验
sudo make install # 安装 在Linux中安装Sodium库:
wget https://download.libsodium.org/libsodium/releases/libsodium-1.0.18.tar.gz
tar -xvzf libsodium-1.0.18.tar.gz
cd libsodium-1.0.18
./configure
make # 编译
make check # 检验
sudo make install # 安装 在Linux中安装PBC库(仅作为学习):
wget https://crypto.stanford.edu/pbc/files/pbc-0.5.14.tar.gz
tar -xvzf pbc-0.5.14.tar.gz
cd pbc-0.5.14
./configure
make # 编译
make check # 检验
sudo make install # 安装
cd /etc/ld.so.conf.d
sudo vi libpbc.conf # 编译好pbc库后,加入libpbc.so.1的路径
cd /etc/ld.so.conf.d && vim libpbc.conf # 将 /usr/local/lib 输入到libpbc.conf文件中
sudo ldconfig # 更新cache
遇到库无法安装的问题,可能是缺少相应的软件,尝试检查g++, m4, flex等软件。
2.2 编译配置
注意:由于我是在Linux上进行开发和编译,虽然后来成功移植到我的Windows电脑上,如果编译出现问题,可能的原因是我的计算器中使用的函数在Windows MinGW上可能不是标准C库的一部分。
计算器标准版编译:
gcc src/haibin_calculator.c -lm -o haibinCalculator -fopenmp -lgmp全部使用了我自己写的功能,可以做到普通加减乘除,大整数加减法和乘法,指数运算。lm表示使用数学库,进行开根号等运算。
更多编译选项:

Part 3: 功能演示
1. 小数字加减乘除
当输入的两个数字有效位数小于8位时,此时计算器会将数字转换为double进行运算。double的精度在 8.85 × 10-15 时,满足我们的精度需求。同时,在计算除法时,除不尽的结果将保留8位小数。
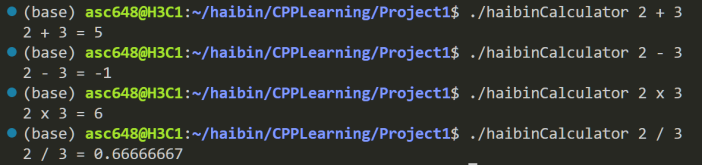
图3.1 基本加减乘除
2. 大整数加减法,乘法
当两个数字的有效位数超过 8 位且没有小数和指数 e 时,计算器将自动转换为大整数模
式。计算器将数字转换为 char*并进行类似于数组的加减法,从而实现大整数的加减法和乘
法。大整数除法的实现过于复杂,由于时间紧凑,我就花更多时间放在了自己更想探索的地
方,没有实现除法。
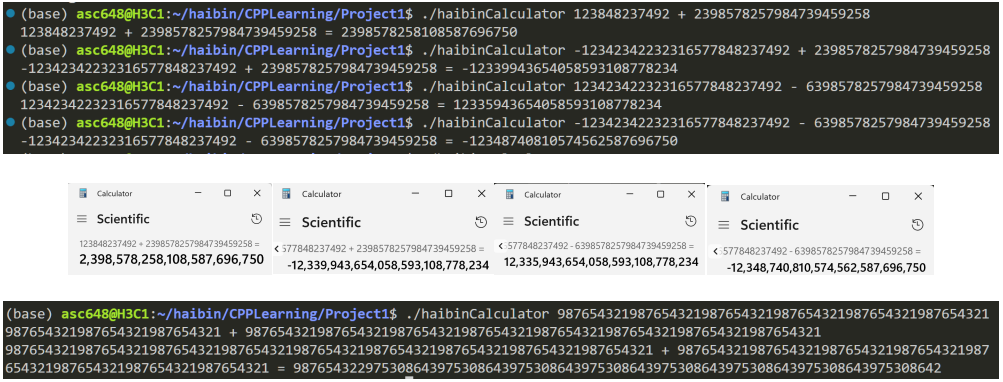
组图3.2 大整数加减及校验
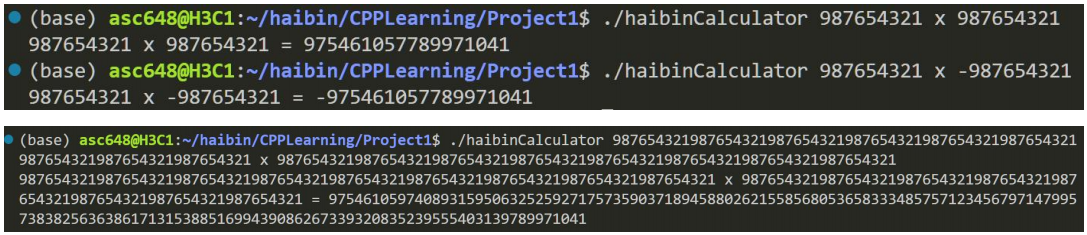
组图 3.3 大整数乘法
由于大整数加减实现时采用的是指针的形式,因此只要内存足够,就可以对超长位数进行加减。这里由于微软计算器已经超限,就没有验证数值。
3. 指数运算
当两个数字都是指数时,将进行指数运算。对于指数乘法,在 e 前的参数采用double
运算,在 e 后的参数使用 double 相加减。除法类似,核心基于 double 的除法。对于加减法,
先将两个数字的指数大小保持一致,e 前的参数采用大整数加减法。

4. 提高性能:CUDA 和 OpenMP
我们的大整数乘法是用大整数加法和移位实现的,计算复杂度为 O(N ∙ M), M,N 为两个数字
的位数。幸运的是,我们可以使用CUDA与OpenMP,将乘法过程并行化,我们将在后面演示。


5. Human Computer Interaction:人机交互
支持 Mode2:等待输入模式
如果我们的计算器在调用时没有输入任何参数,计算器将进入另一种模式,它将等待用户的
输入并进行计算。计算的效果与直接调用模式相同。
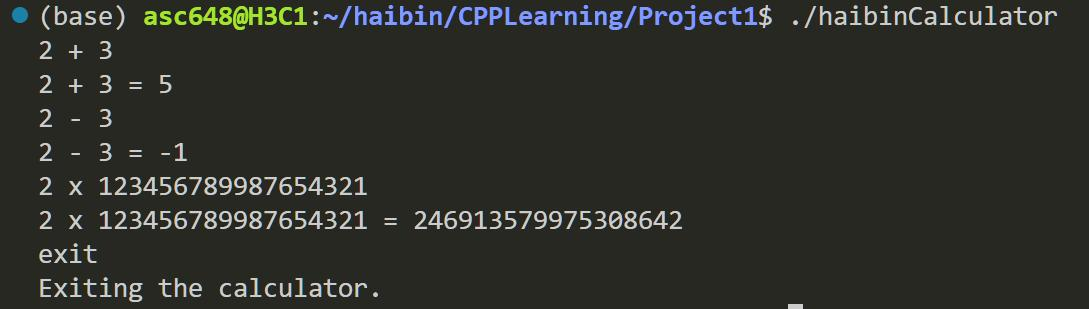
-v / --version
打印计算器版本,显示计算器编译时间,并打印世界线常数设定。
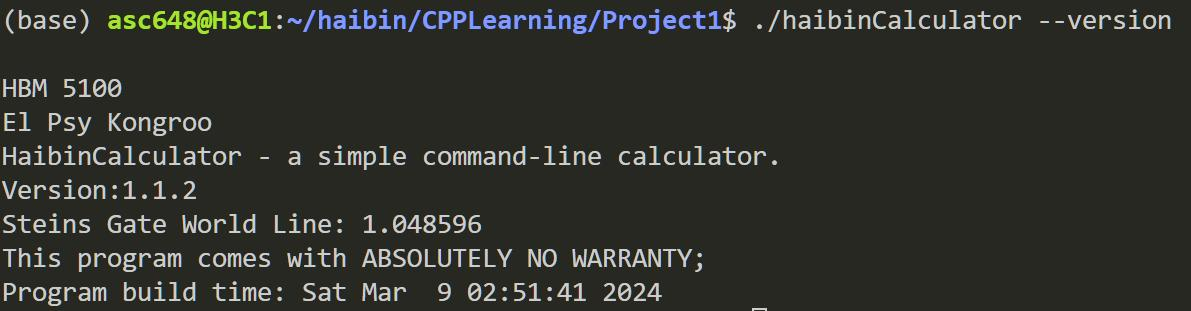
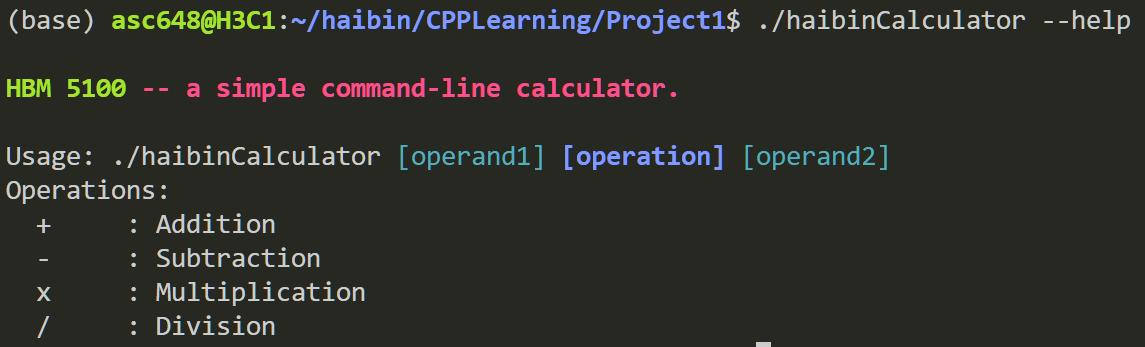
-h / --help 打印五彩斑斓的帮助
-l / --mathlib 打印计算器使用的数学库

cls / clear 调用 system(“clear”) 清空屏幕
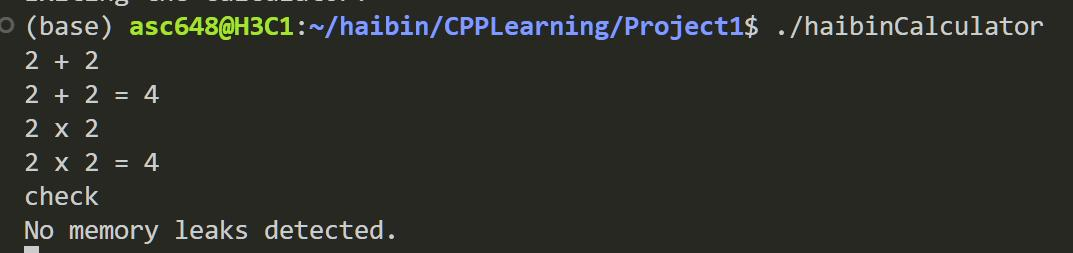
check 检测计算器内存泄露
cmatrix 调用一个好玩的软件包(sudo apt install cmatrix),变成黑客帝国,ctrl-c 退出。
Part 4: 需求实现:路上的困难
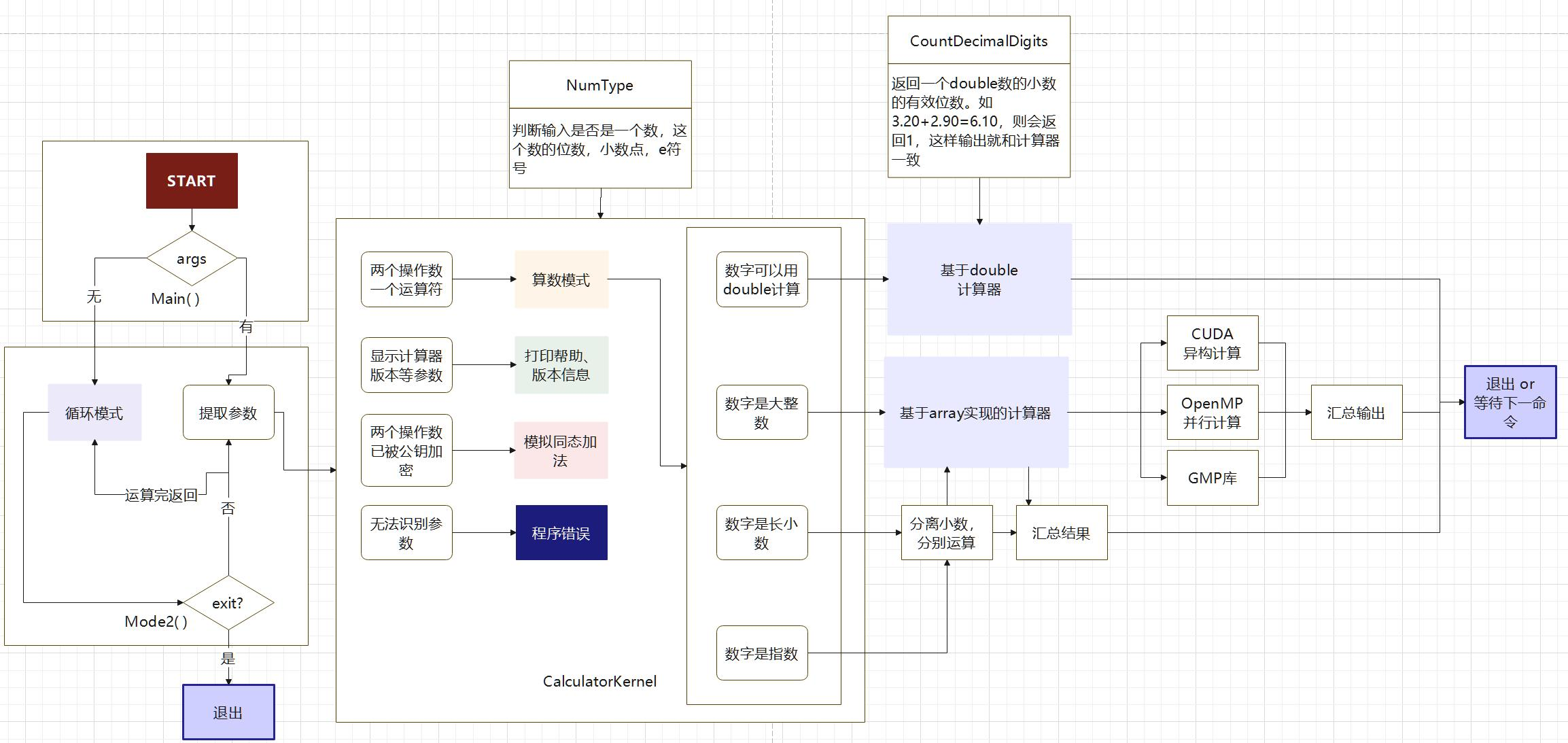
本次 Project 项目结构如下,从 main 函数启动后,根据参数判断模式,判断执行命令。
如果是计算命令,就会凭借数字类型进行具体计算。
4.1 输入 x 还是 * ?
我的 Project 开始于对输入的处理。main 函数会根据空格分隔出几个字符串,随后计算
器将判断输入的字符串数量。
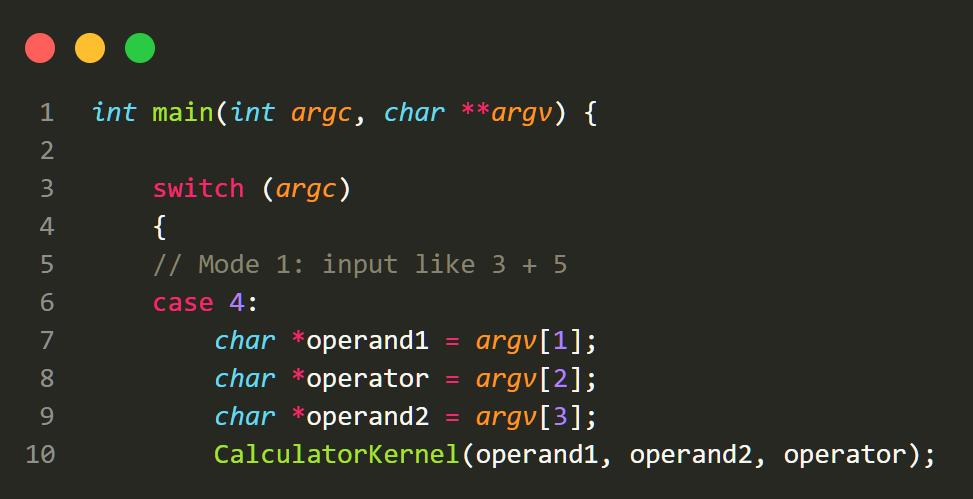
图 4.1 main 输入判断
但是当我输入 3 * 5 时,我发现 argc 变量并不是我想的 4 个。随后进行测试,发现”*”号
会读取当前文件夹下所有的文件作为字符串输入。原来,代表乘法的 ’*’ 号 在 Linux 系统中
会被识别为通配符。

图 4.2 判断 * 输入
在经过讨论后,且在老师的同意下,我认为使用 x号相比使用*号然后做各种处理会
更好:
第一,只有输入3 ‘*’ 5才能被专门识别为乘号,但是为了乘号多打两个单引号很麻
烦。如果单纯忽略,只读取最前面的 3 和最后的 5,也感觉非常不妥。
第二,这个问题跟安全有关:不同的用户有不同的目录,如果有人依靠我的计算器输入读取了他文件夹下的所有文件,说不定别人就能通过攻击我的计算器查看到他的文件。
我后来也去查找如何修改这一配置,我们可以去修改 shell 的配置文件,进入~/.bashrc
文件,并用命令: set -o noglob 禁止通配符展开。然而这样的修改变动太大,为了一个计算器得不偿失。
因此使用”x”符号作为乘号。
4.2 Mode2 的输入
在 mode2 下,我们要等待用户输入,然后执行相应的计算指令。

我一开始用的是 getline 函数,这个函数在 stdio.h 中。但是,当我把这个函数移植到
Windows 的 minGW 时,它显示 Windows 上编译器没有这个函数。我随后用了 fget 函数。
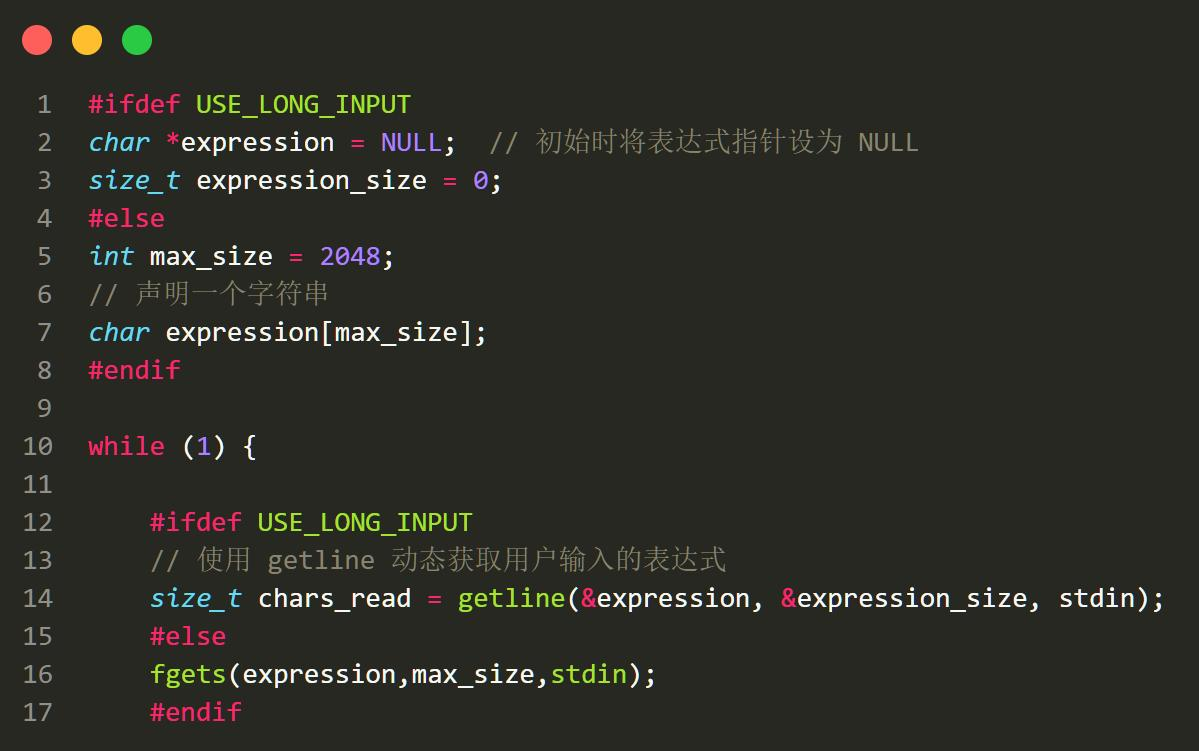
采用 fget 函数的代价便是会有长度输入的限制,不过这也让我好奇不同函数他们是怎
么处理输入的。
简书一篇博客 C中读入一行字符串的方法讲的挺好的,它对比了scanf,gets和fget三种函数的区别。scanf是非常邪恶的,我们给他长度为6的char数组,然后输入8个char,结果它会在数组后继续填写数字。也就是说,会覆盖我们的内存。而gets的 原理
和 scanf 相同,只有 fget 函数才能保证内存上的安全,并且能读 stdin 和文件。
4.3 IEEE754: 深入了解浮点数
刚开始实现计算器时,我发现 matlab 和我的 CASIO 计算器在正常情况下用的都是 double
进行计算。double 真的够精确吗?抱着这个疑惑,我阅读了 double 的标准:IEEE754 。

在 IEEE754 标准中,正如我们学习的那样,double 是使用 1 位表示正负,另外的位数表示如下图。

在此之外,我还发现了一些关于浮点数里有趣的事情。比如浮点数里的 NaNs 是用
1111...11 表示的,当我们使用 0/0 时,会出现这个结果。我想跟除法的运算性质有关。不过,
跟 Infinities 比起来,无限这个数的 N-1 bits of Significand 是 0。另一个有趣的点是浮点数是
区分正零和负零的,跟我们在数字逻辑里的二进制表示整数的方法并不一致。
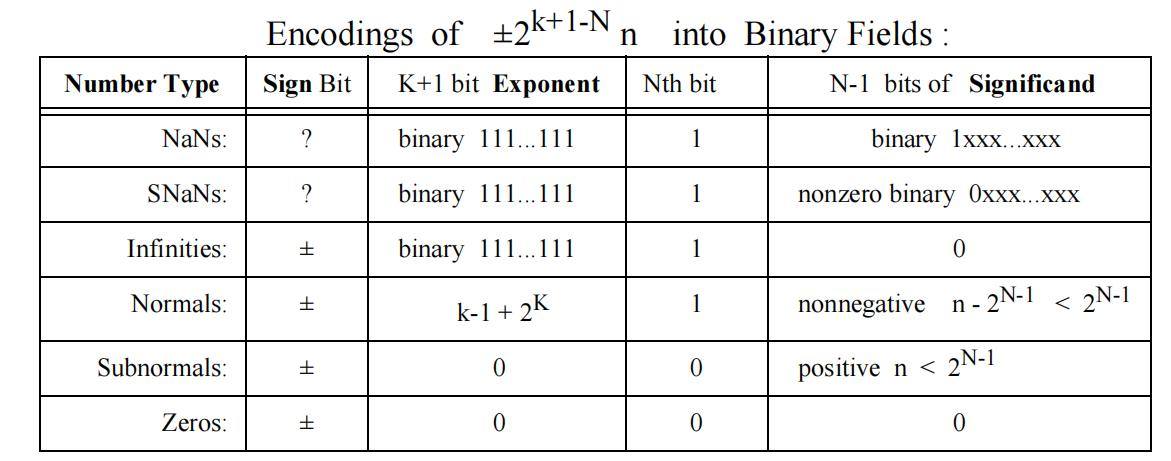
这里还有几个有趣的运算,比如 1 的无穷次方不是 1 而最好是 NaN,但是 0 的 0 次方却
是 1 而不是 NaN。为了引入这个诡异的 Not a Number,标准对待它就像数据库对待 NULL 一
样谨慎。

看过标准后,我们这里主要处理的,就是 0/0。在 8 位有效数字下,最大的两者相乘也
是 16 位,我们就可以都用 double 表示。
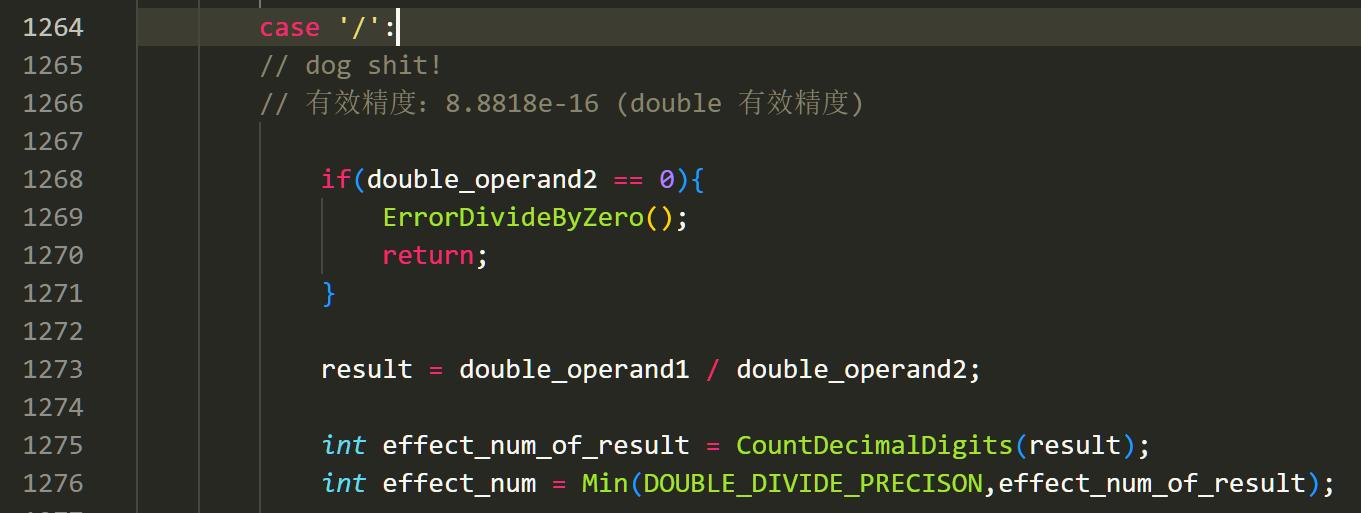
在此以后,面对小运算,我们就可以“偷个懒”,用计算机自带的 double 计算完成运
算。但是,怎么打印出来,成为了我下一个问题。
4.4 如何精确打印浮点数?
是的,浮点数其实并不是很好打印。0.1+0.2 = 0.300000004,这本质上涉及到进制的问
题。我们在 10 进制下十分之一是一个有限小数,但是 2 进制下十分之一和五分之一都是无
限不循环小数,而用 double 相加后,自然会产生一个误差。但是,如果我直接打印,
0.1+0.2=0.30000004 很明显是不对的。并且,如果我们直接使用 printf(“%s”,Number),我们
得到的是保留小数点后 6 位的 double 输出。比如 2.8+3.2 = 6,但是我们的浮点数计算器会
输出 6.000000。

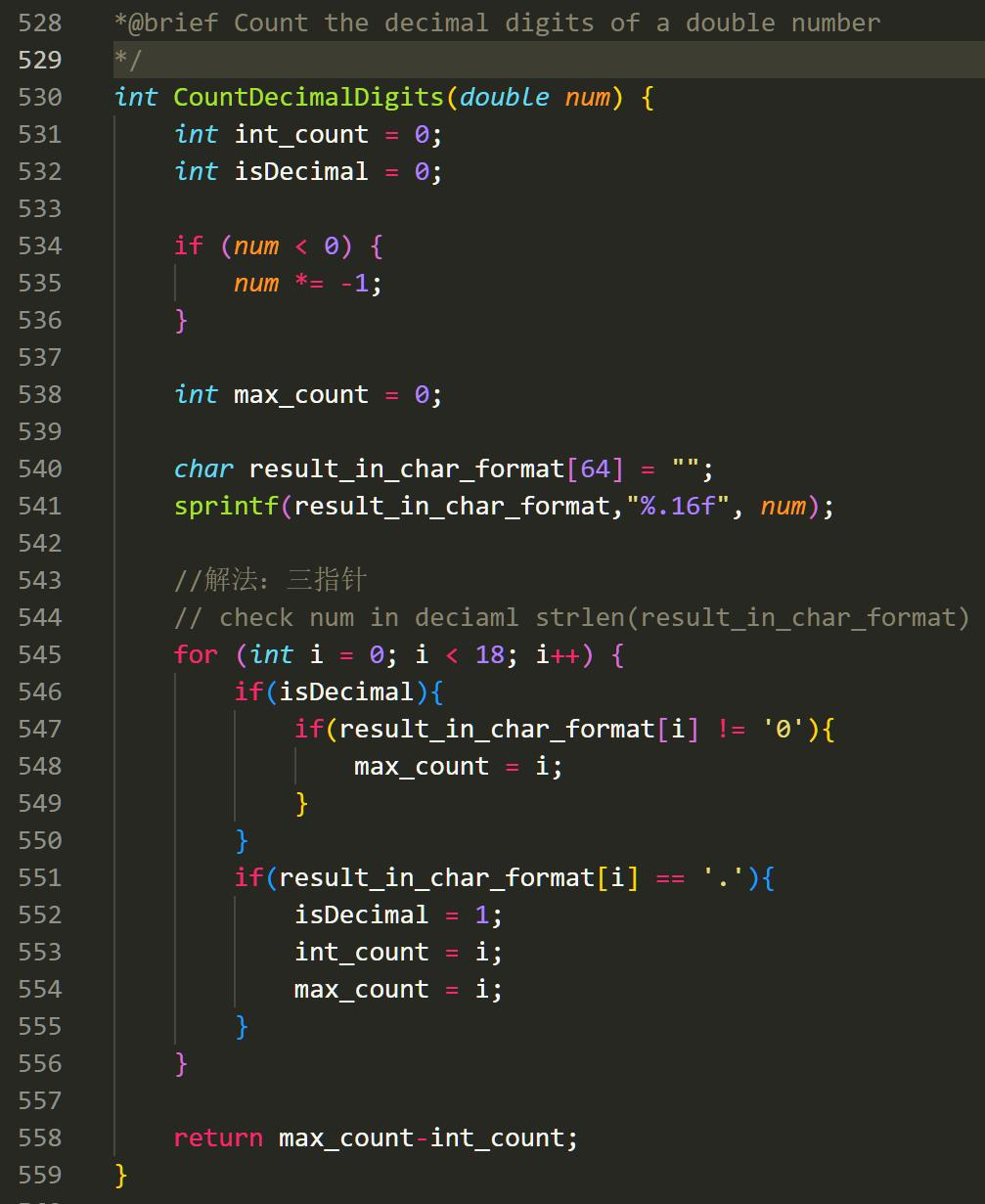
那么这应该怎么做呢?我设计了一个方法 CountDecimalDigits,使用三指针判断一个数
的有效位数。这个方法将返回 double 的小数里最后一个不是 0 的数的位置。在处理过程中,
我会将 double 临时转换成 char 数组,然后在数组内进行操作。使用了这个方法后,就可以
打印浮点数了。
不过,假如我们算出来的数字与我们的 double 表示方法不一致,printf 是如何快速转换
和打印浮点数的呢?就比如说 2/3=0.66666667,假如保留不同的位数,输出的结尾都会四舍
五入一个 7,这是怎么做到的呢?我去看了文章[5]《如何快速打印浮点数》,大概发现了一
些答案。

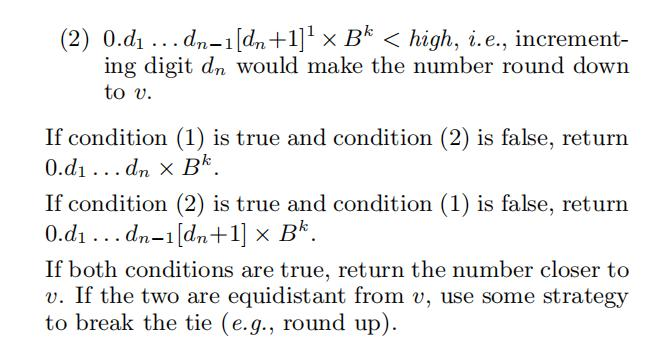
在这篇文章里作者提出了一个打印算法,它的操作有点像数学里的牛顿法,每一位都尽
可能贪心地逐步逼近我们的真实值,直到用完 double 里的所有可表示位。文章还进行了有
效性的数学证明与伪代码,我就看了最后的数学证明就溜了。
这项知识很有意思,因为在 java 的时候,我从没有考虑计算机的底层会怎么实现这些打印,我们所度过的每个平凡的算法,也许就是连续发生的奇迹。[[如何精确打印浮点数 文章导读]]
4.5 Numeric Implementation: 仿 Postgresql 的 numeric.c 实现的大数计算器
使用 double 时,无法计算大位数的乘法如987654321 x 987654321 。为了计算大数,必须采用新方法。
但是新方法如何完成?我在构思是否可以用数组实现。这时,老师提示我在数据库里,刚好有人实现了这样的精确大数计算。于是,我去查找了 Postgresql 的 source code,专门去研究了它 numeric.c 的实现。不看不知道,一看吓一跳,这 numeric.c 的加减乘除,还有类型转换,Postgresql 竟然写有 12000 行!
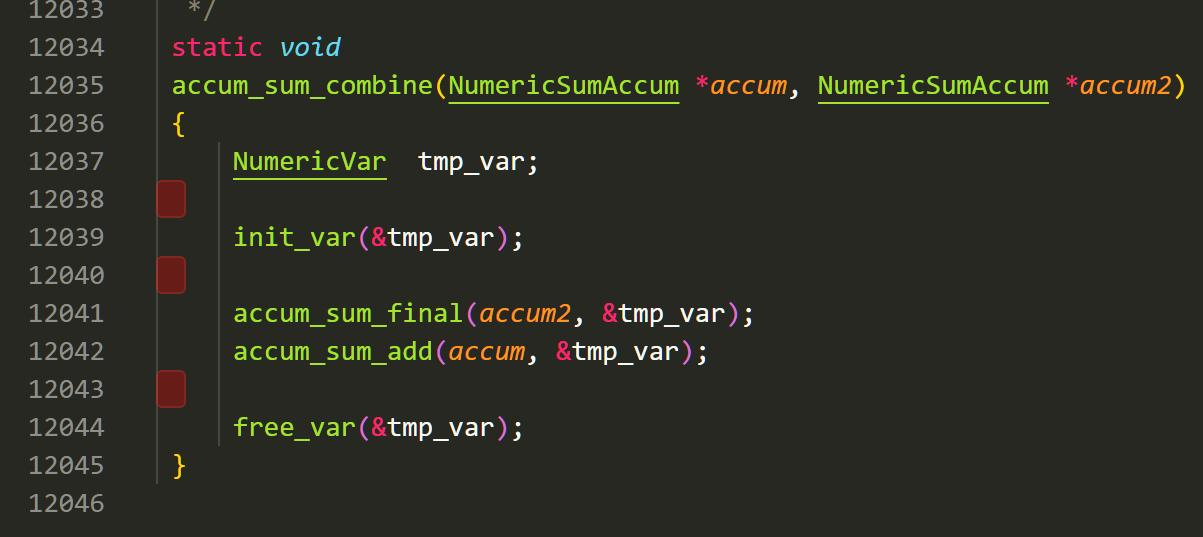
我将代码复制了下来,顺便把零零散散各种定义,结构体,宏文件也复制下来,看了三
天三夜......我估计总代码量就已经超过 2 万行了。比起我自己的“计算器”,那是真的简单又幼稚啊,“朝菌不知晦朔,蟪蛄不知春秋”,可能说的就是如此吧。
但是幸运的是,在这之中,我找到了 numeric 的方法 add_var 的实现。仔细研究后,我大概明白了它的工作原理。
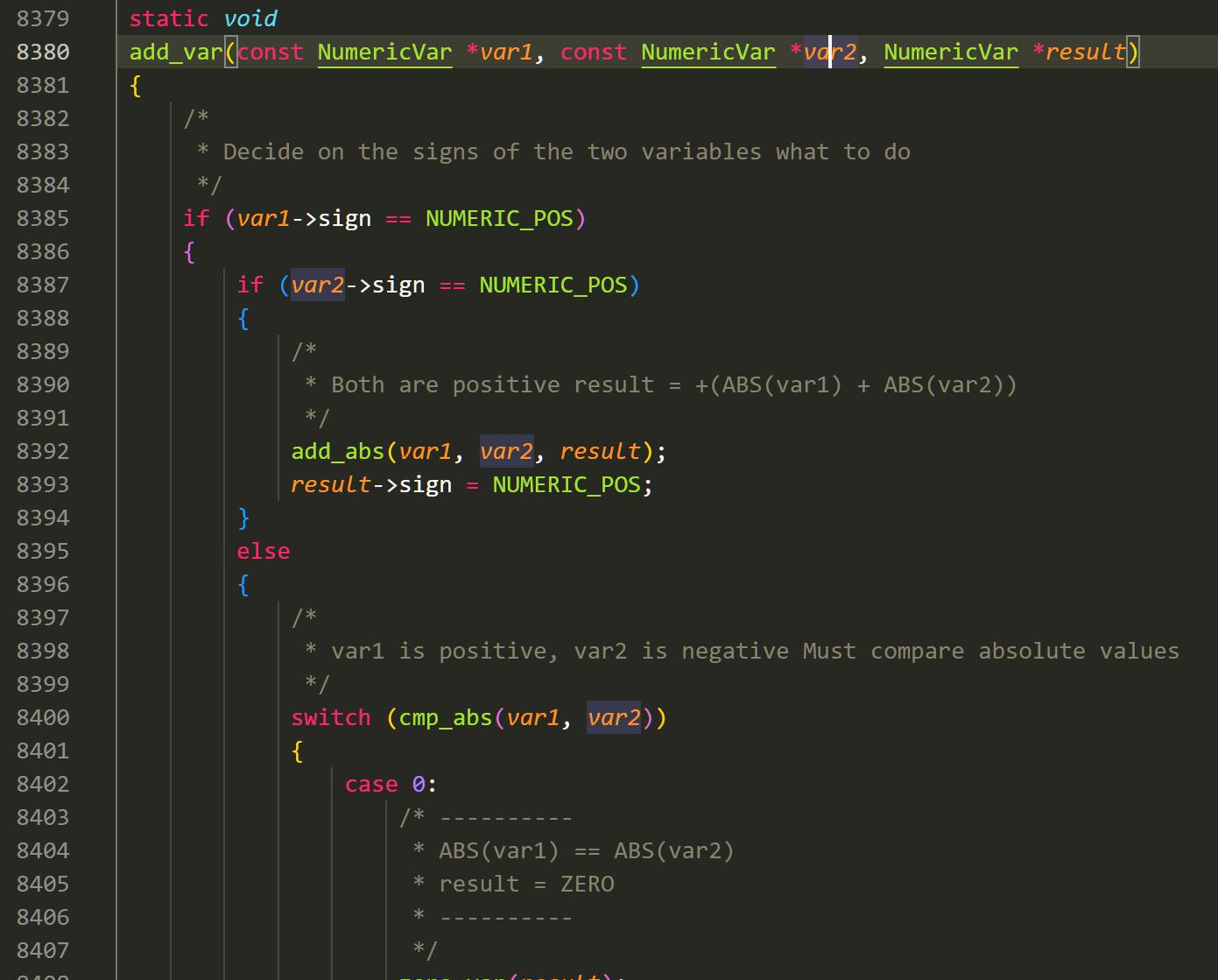
在这里,Postgresql 首先先不管符号,实现了 add_abs 和 sub_abs 方法,在这两个基础方
法内考虑两个正数相加,以及大数剪小数。之后,add 和 sub 分别会考虑正负性,在输出时
加上正负号。另外,在 Postgresql 内所有类型的传输都是依靠结构体进行完成。
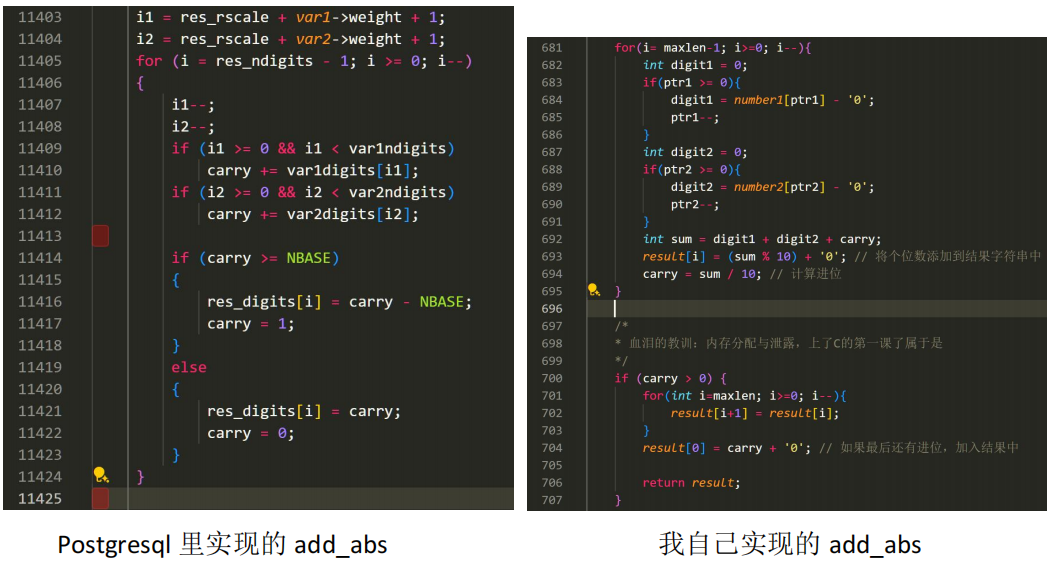
因此,我依照 Postgresql 的方式,顺利完成了大整数加法和减法的设计。但是乘法怎么
做呢?我继续去读了源代码。具体的思想便是,它会将每个数字单独相乘,然后将结果像矩阵一样竖着相加。
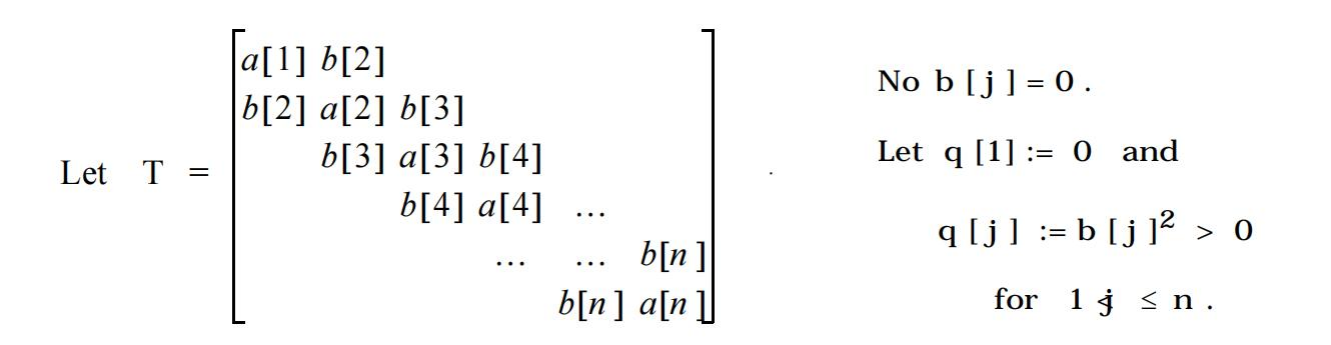
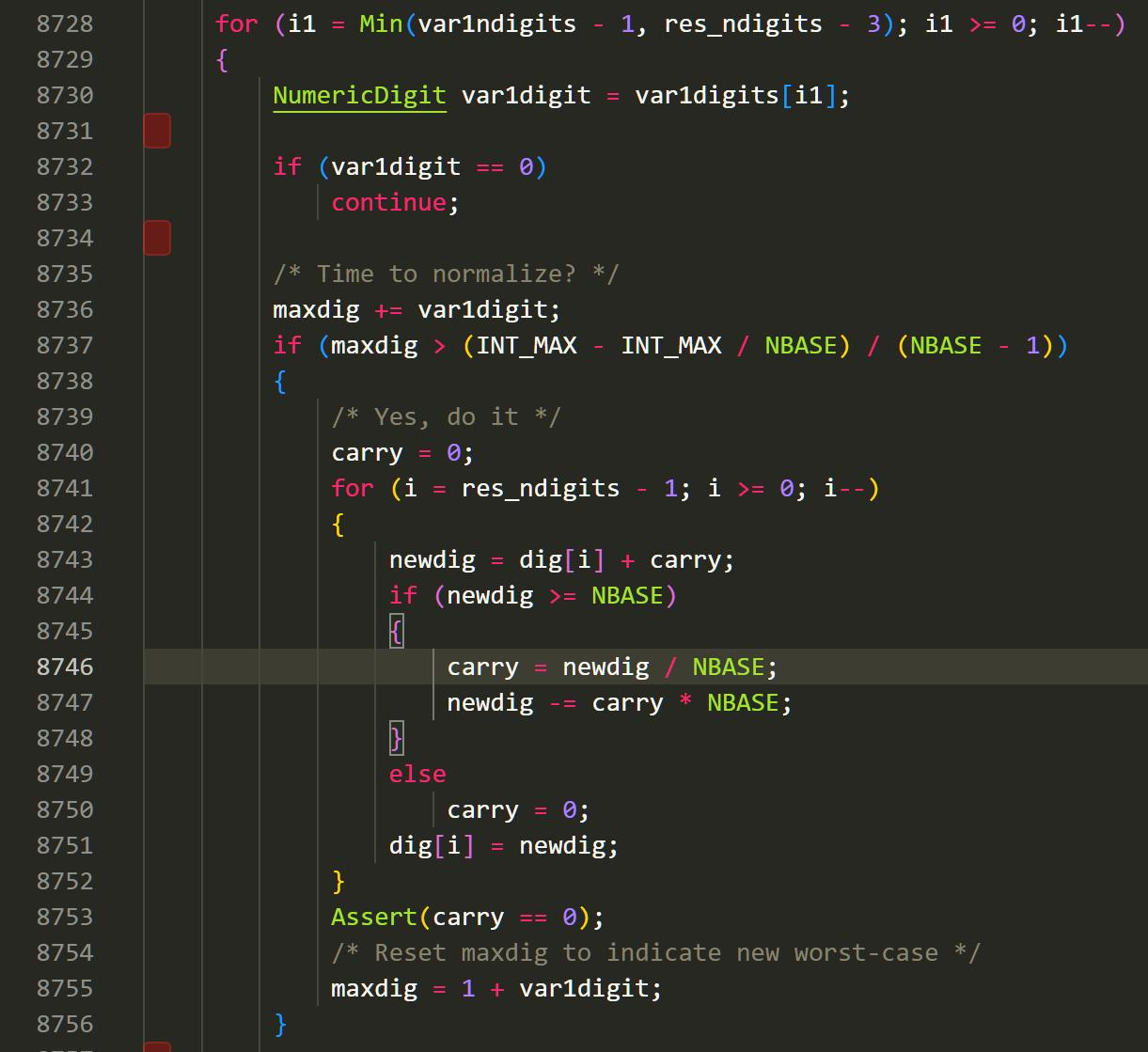

这里边它的计算复杂度是 O(n2),使用了两个 for 循环。在第二个 for 循环里,它将我们的矩阵逐步相加。不过这个 A[i] += B * C[i]的公式我可太熟悉了,这不就是我们的并行计算里最标准的并行化算法吗!看来如果想优化,我们可以从这里入手。当然,我猜测考虑到通信成本的问题,在这个第二层的 for 循环搞并行化一定是得不偿失的。大概看完代码后,我实现乘法决定这么实现:对于数 A x B,我们先用 B 中的一位 var_digit分别去乘上 A,也就是用一个数乘一个数组(multiply array x num),然后我们通过 var_digit所在的位数,将我们的结果进行移位(shift),最后把我们的结果加到我们的 result 数组上。这样的操作是和 Postgresql 里的操作基本一致的。
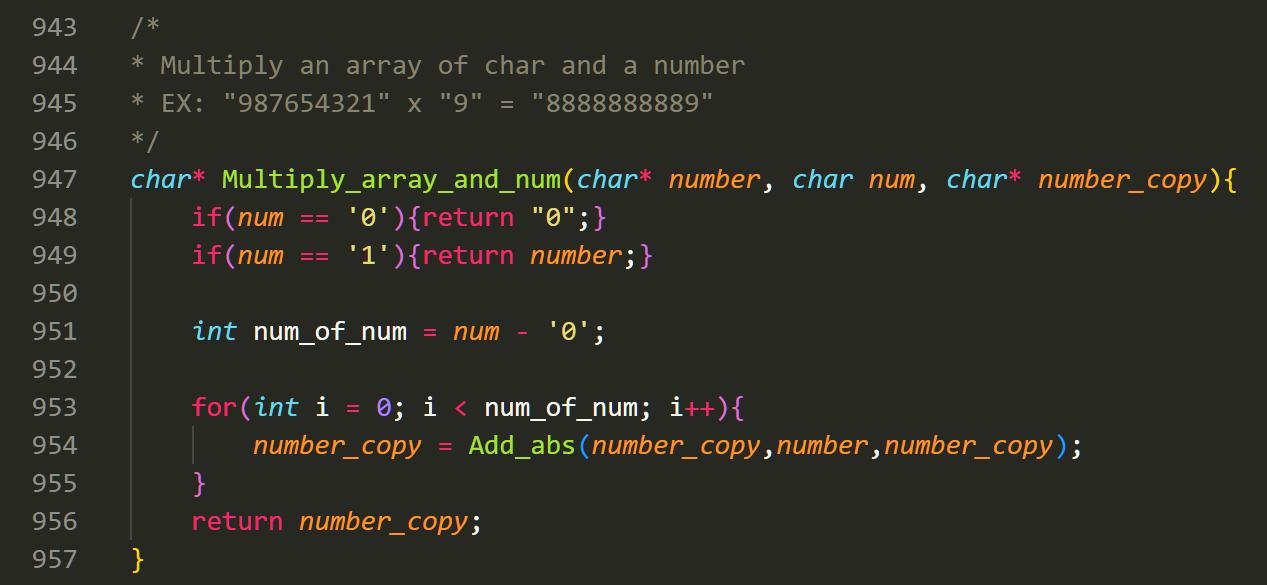
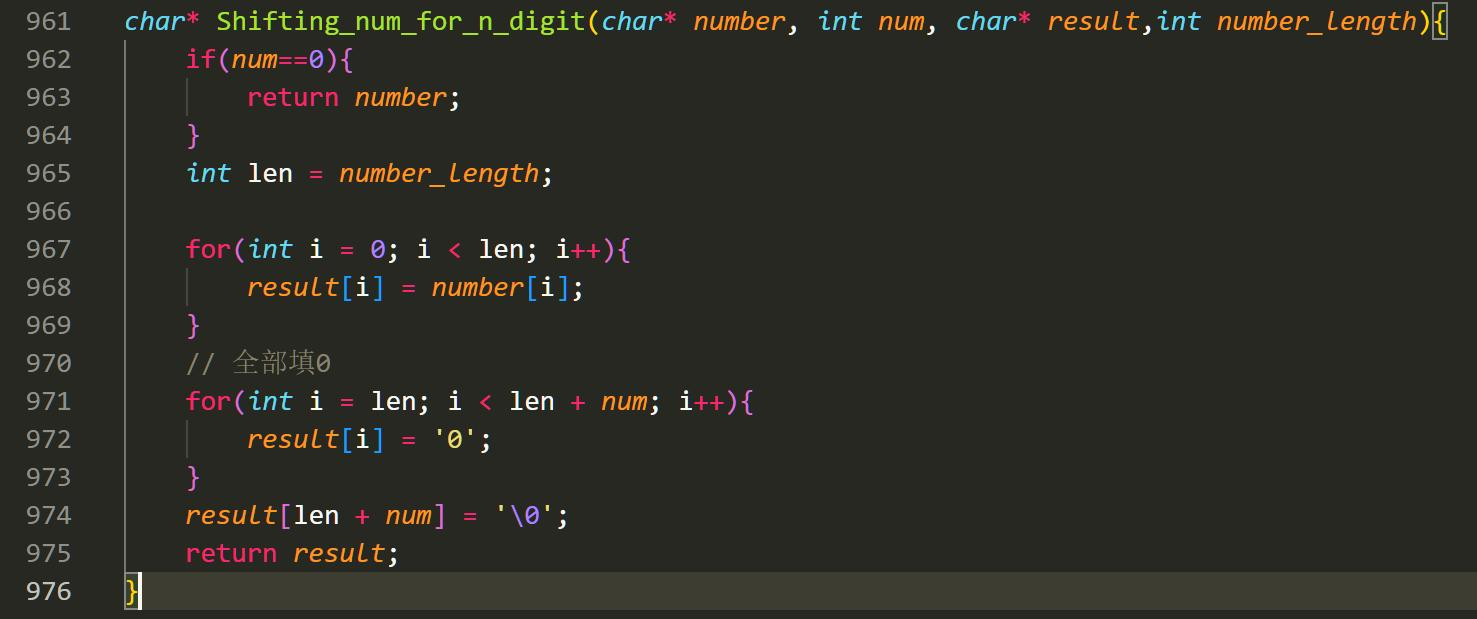
这样,我们就通过 array,实现了大整数的乘法。这里我画了一张实现的图,它阐述了各个
方法之间的关系。
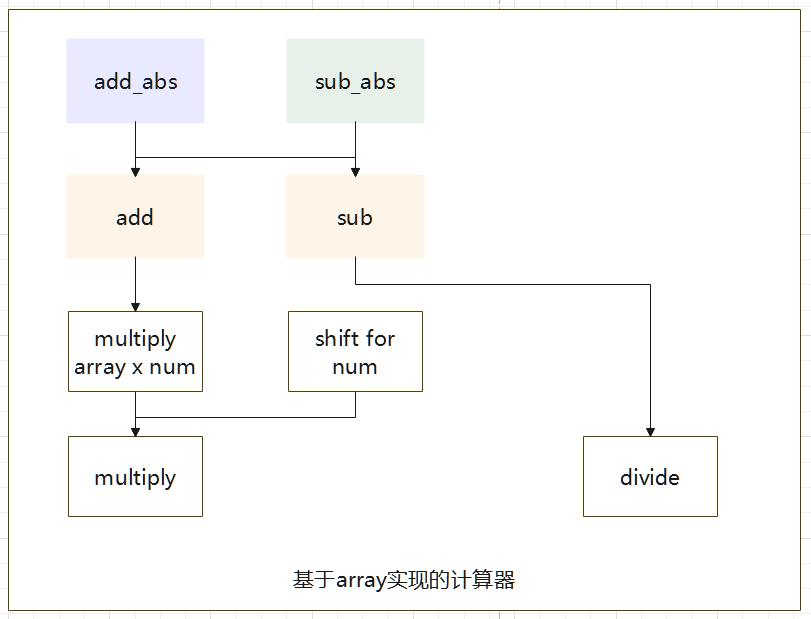
除法我没有实现,针对除法的整数部分,我们可以直接列竖式移位相减。不过我暂时没有想明白,小数点应该怎么处理。
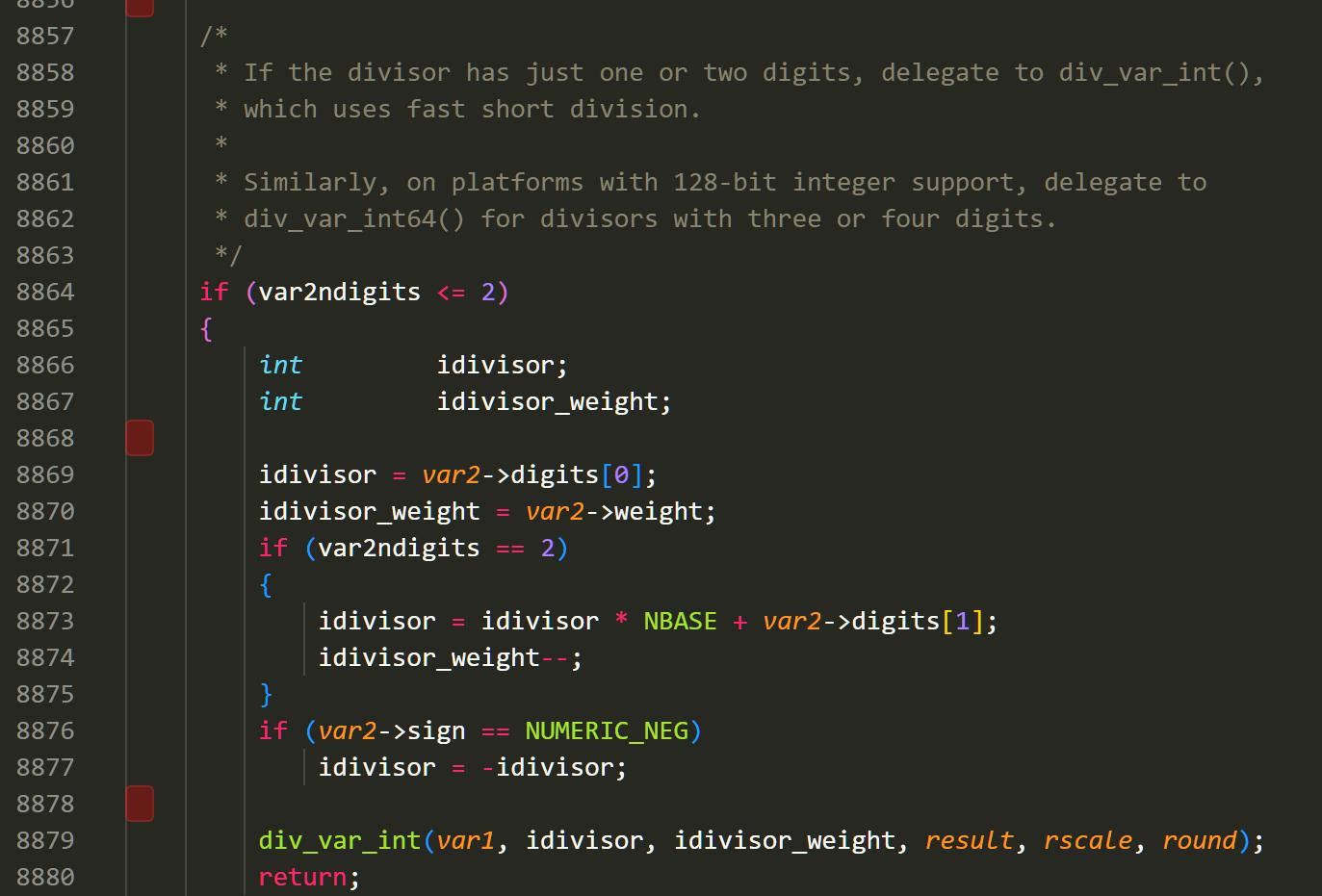
Postgresql 里除法的实现内容
PS: 回过头来看,高精度大整数除法没有想象中的那么困难。我们可以针对我们需求的精度,按照需求精度进行移位。当我们的所需精度都保证在除法的整数部分后,再相除,最后再移位小数点,即可输出对应的结果。因此,在除法中,精度很重要。
有很多的除法算法喜欢分成高精度除以低精度(短除法),高精度除以高精度两种情况并分开实现。两者的区别在于,第一种由于精度较低,在获取完所求的精度后,便可直接退出计算。如300位有效数字除以5位有效数字,其大部分计算算至6-7位即可。
在数值计算除法大致可以分为两类:
慢速算法:每步只能确定一位的算法。长除法属于此类,时间复杂度为O(n2)。
快速算法:每步可以确定多位的算法。牛顿迭代法属于此类,配合用 FFT 实现的乘法,时间复杂度为O(N × log N),其思想为逼近。(FFT的文章:)
大整数的加减法跟 double 的加减法是不一样的。同样是一个加号,两者在最后的实现操作完全不同。我们是不能直接因为在草稿纸上脑子一动,就理所应当地认为他们的加法是一样的。
这让我想起在上学期的离散数学里老师讲的群环域的知识。double 所表示的数跟加法运算构成阿贝尔群,大整数所表示的数跟加法构成另一个阿贝尔群,这两个群的 基数Cardinality 并不相同:大整数群,也就是整数加法群,是个无限群,基数为ℵ_0,而 double 的Cardinality 为232,找不到一个在两群之间的单射函数,因而他们是不同构的。不过,是否存在一个函数 f: G->H ,使得 集合G内元素a,b 有 f(a+b) = f(a) + f(b) ,使得他们构成同态呢?
我们可以用加法群的单位元0来操作,令 f(x) = 0,即可说明。不过,即使他们两者同态,这也不能在算法上说明什么。浮点数中比较致命的事情是精度损失,这是整数加法所没有的。
4.6 Karatsuba 大整数乘法探究
有没有比相加然后移位更快的算法?我专门上网找了一下,还真有。知乎的这篇
Karatsuba大数乘法算法 - 知乎 (zhihu.com),就介绍了多种乘法运算。我们刚刚
使用的,仅仅是小学模拟乘法,列竖式相加。而其中使用 FFT 的 Schönhage–Strassen algorithm,
复杂度可以说是已经很少很少!仅仅 O(n logn loglogn)!

至于 Karatsuba 算法,这算是我目前能够理解的算法了。它的核心要义在于,我们以往
的列竖式相加,我们要分别计算 A x D 和 B x C,随后再相加。而他想到了讲这个数变成
(A+B)(C+D)-AC-BD,这样就能用上两边已经运算了的数字,减少了运算次数。假如一个 4 位
数乘 4 位数,我们用小学生办法算要 16 次乘法,而他只要 9 次,这加快了我们的速度。
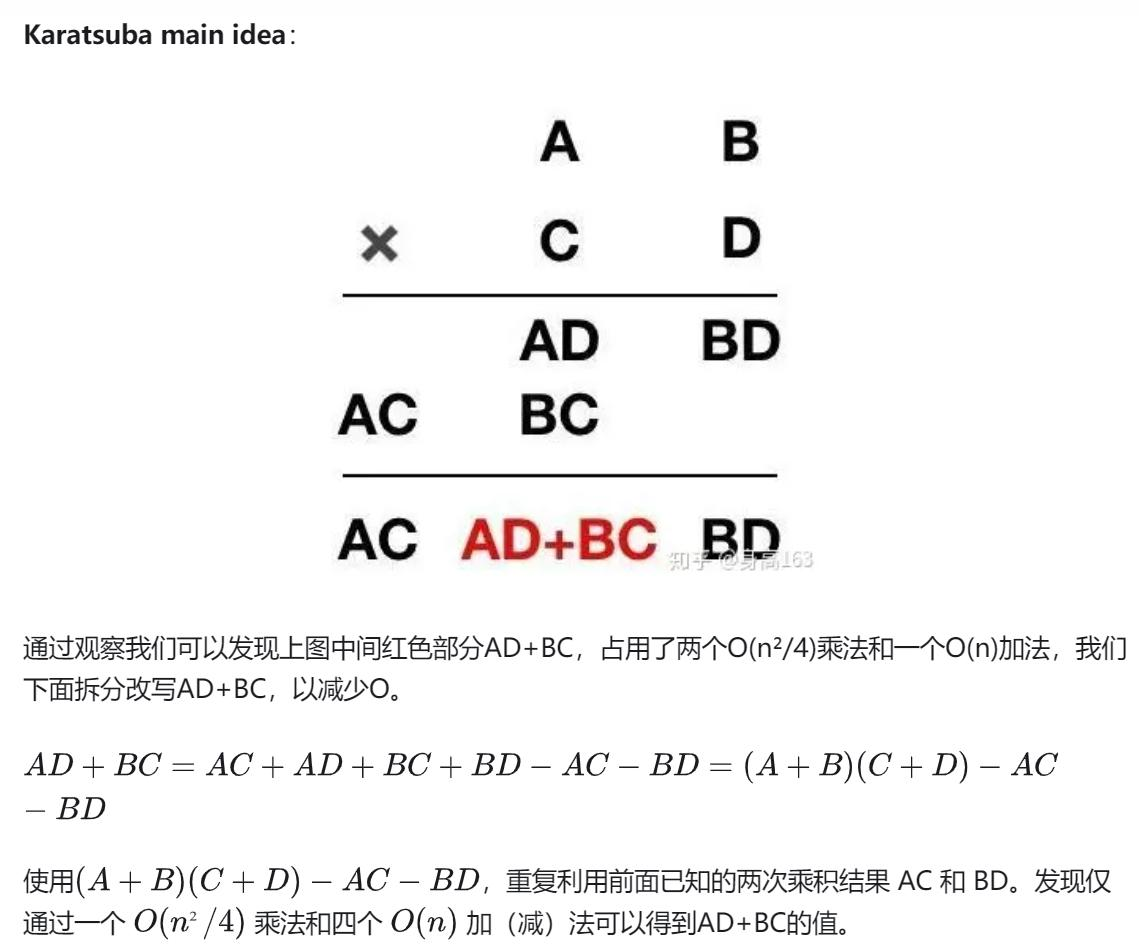
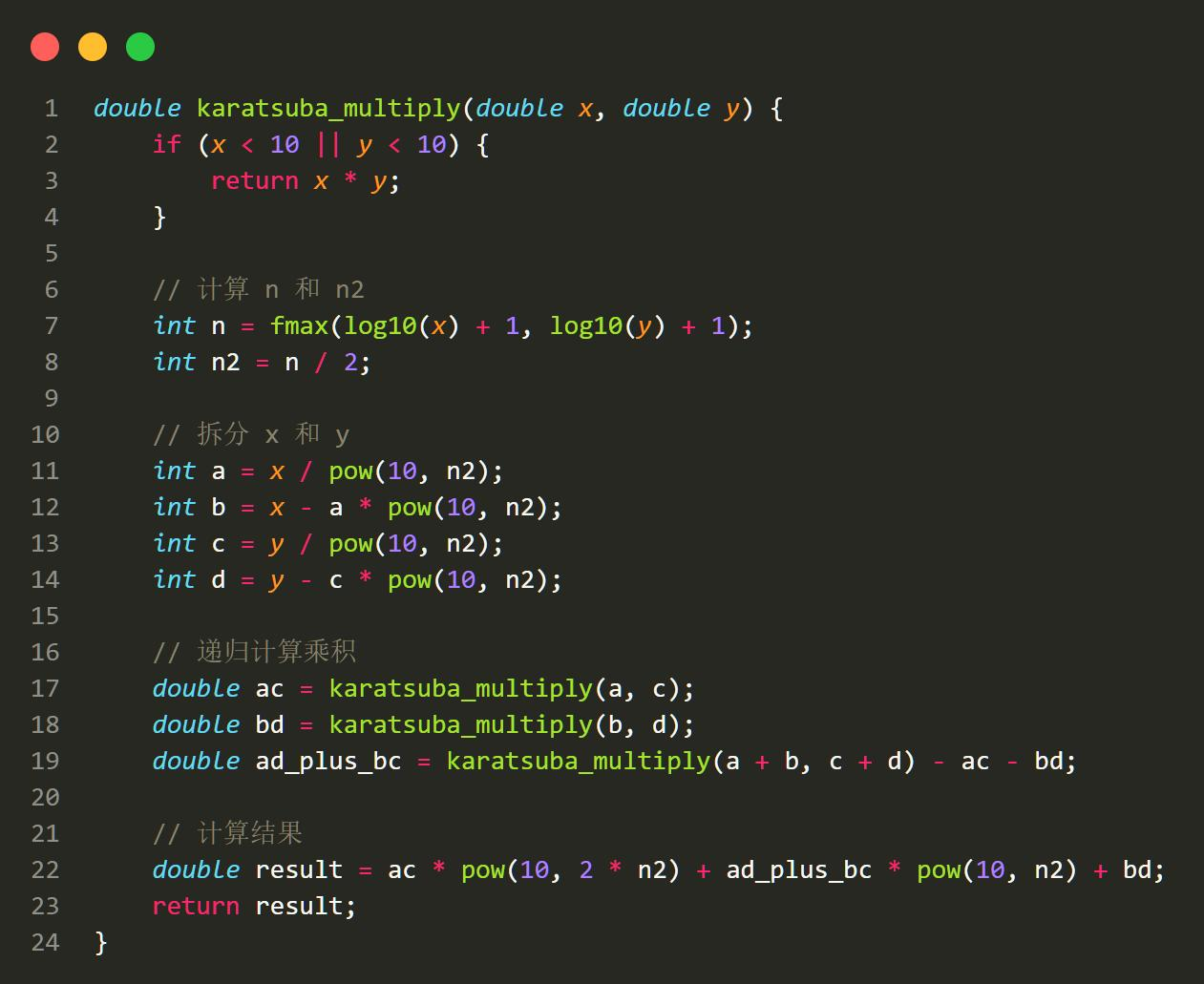
但是,这个算法有个很严重的问题,就是他需要计算对数和指数,这需要新的实现以及
更多的功夫。
Part 5: 内存泄露:Java 最高兴的一集
啊!终于来到了最痛苦的部分。我在这里花费了 4 天 4 夜,也依旧没有解决完这个问题。
这是我有一天看完何泽安学长的 C/C++作业的时候发现的:内存泄露!每当我们在方法里
malloc 时,如果我们不 free 掉这部分内存,那么这部分内存会一直被视为被程序占用,一
直到这个程序终止,这样的话,我们的计算器会随着时间的发展,逐步吃掉我们整个计算机
的内存!
有什么办法可以检测这个问题吗?我找到了一个软件 valgrind,它是一个虚拟 CPU,在
这个虚拟 CPU 上会运行我们的代码,然后检测有没有内存从此消逝了。
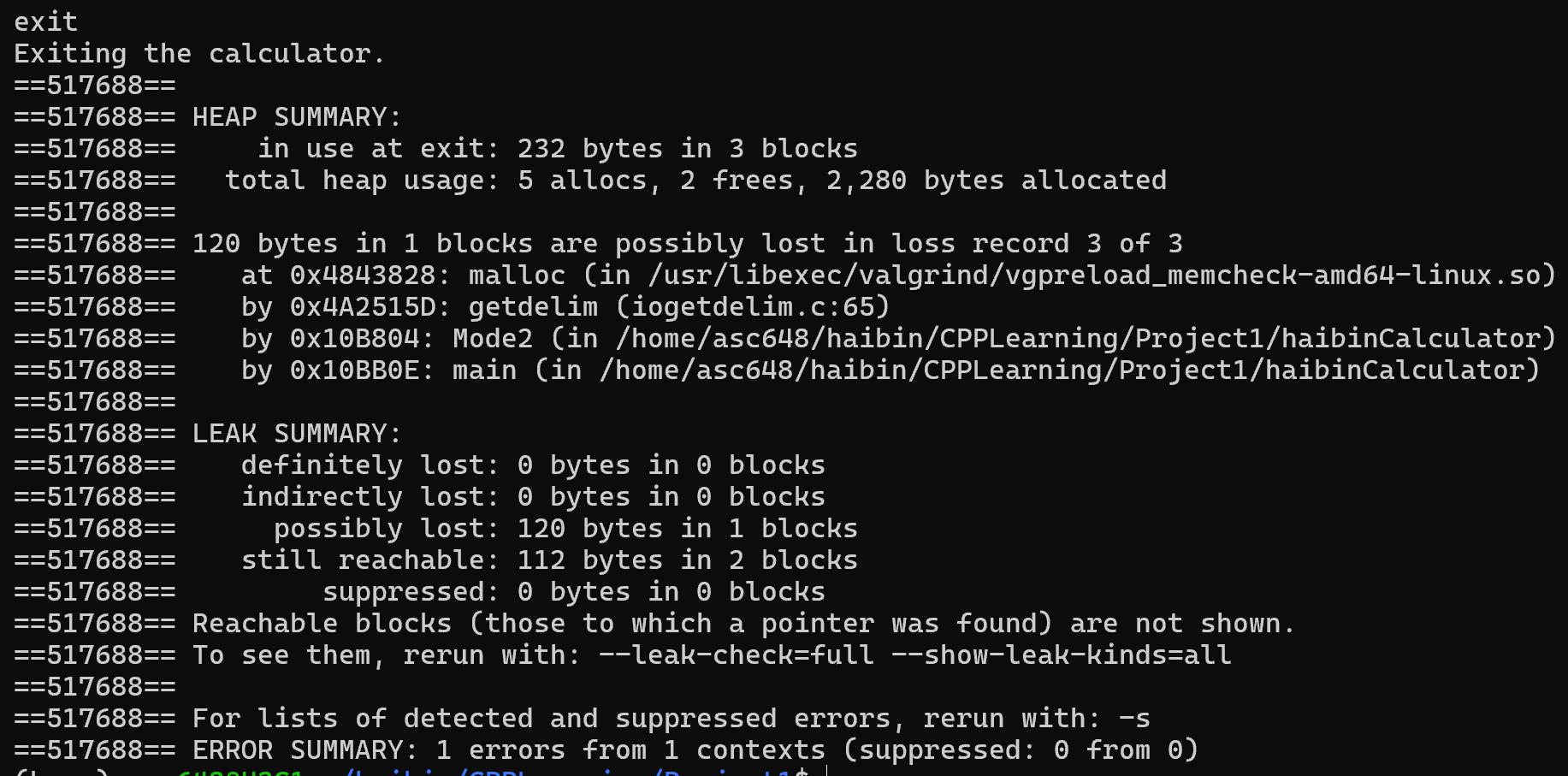
我们用 valgrind ./haibinCalcluator 12345 x 123456,去启动我们的计算器。结果发现,我们的计算器光荣地漏掉了 120byte,可能漏掉了 112byte。
我第一次考虑到这个问题时,前面的方法已经实现完成了,我此时只好去重构。而重构的方法也就借鉴了 Postgresql 里的操作:将代表 result 的字符串也输入进来,在 result 上进行操作,而不是在方法内自己 malloc 一个,不然的话返回的时候是无法 free 掉它的。真是伤脑筋!我瞬间感受到 C/C++的弱点:内存不安全!我又一想到可怕的 Windows 和 Postgresql里有几千万行代码,说不定哪行代码就没有实现内存释放 free。重构花去了我很多的时间去调试和修改,写了一个寒假的 java 后,突然遇到这样的情况,我顿时有一种在屎山里遨游的感觉,我顿时懂得了 Oracle 程序员的心理,太狗屎了!

此时一位明君启发了我。他在他的博客里写明了一种管理内存分配的方法:我们每次要分配一个内存的时候,我们就往一个链表里塞上我们分配内存的指针。在释放时我们将指针从链表中移除。https://blog.csdn.net/weixin_43308899/article/details/135122404
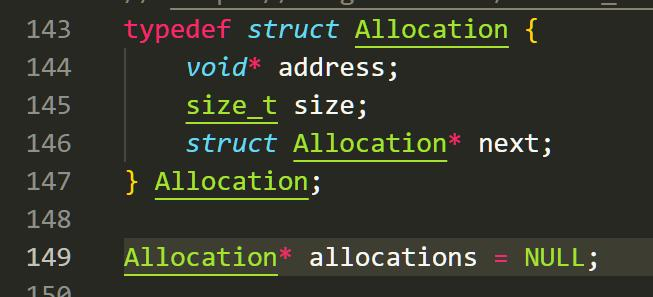
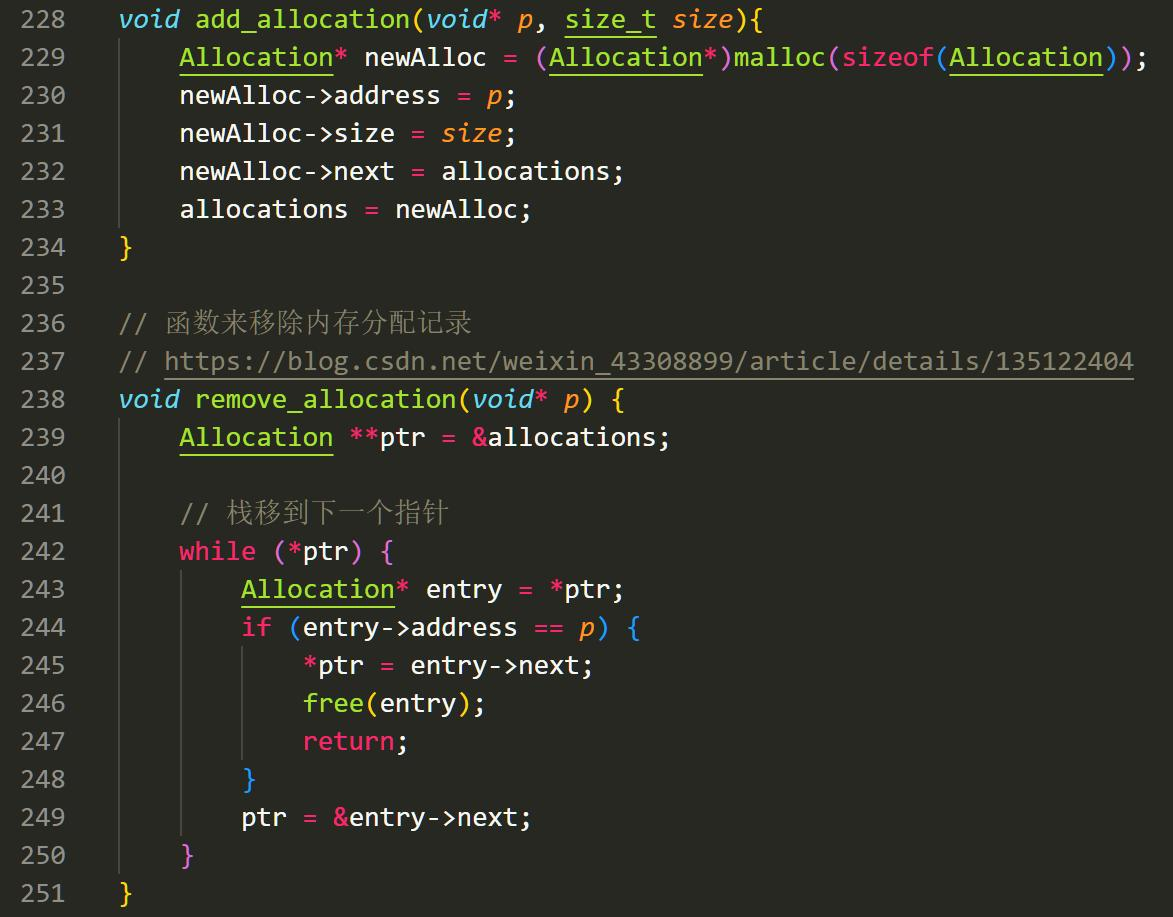
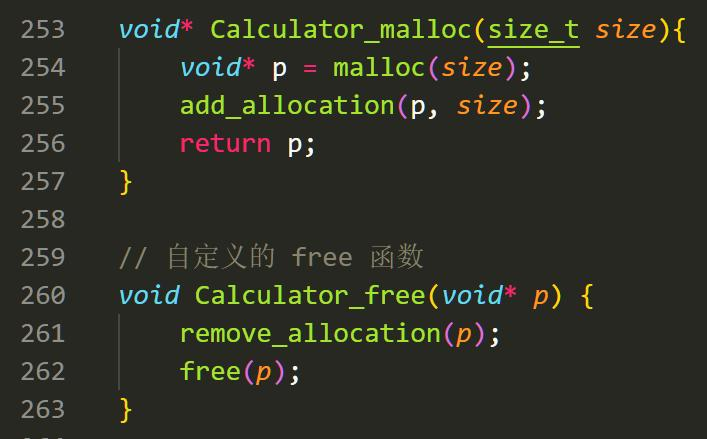
通过这样的方法,我们就可以动态控制我们之前分配的指针。为了方便,我自己写了一个 memcheck 和 clearMem 的函数,他们可以随时监控内存泄露和清空已经分配的内存。
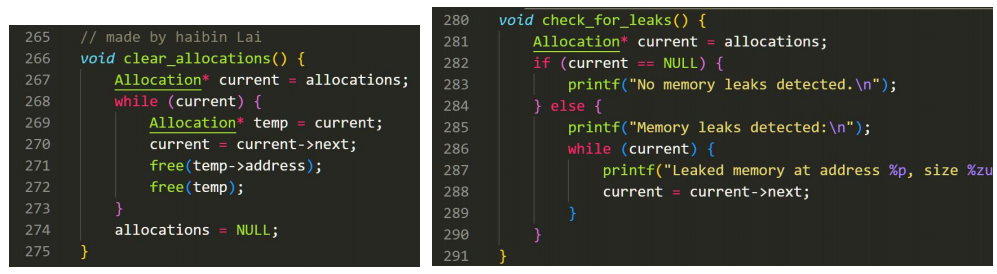
经过我们的一番爆改之后,我们的计算器不会出现内存泄露了。
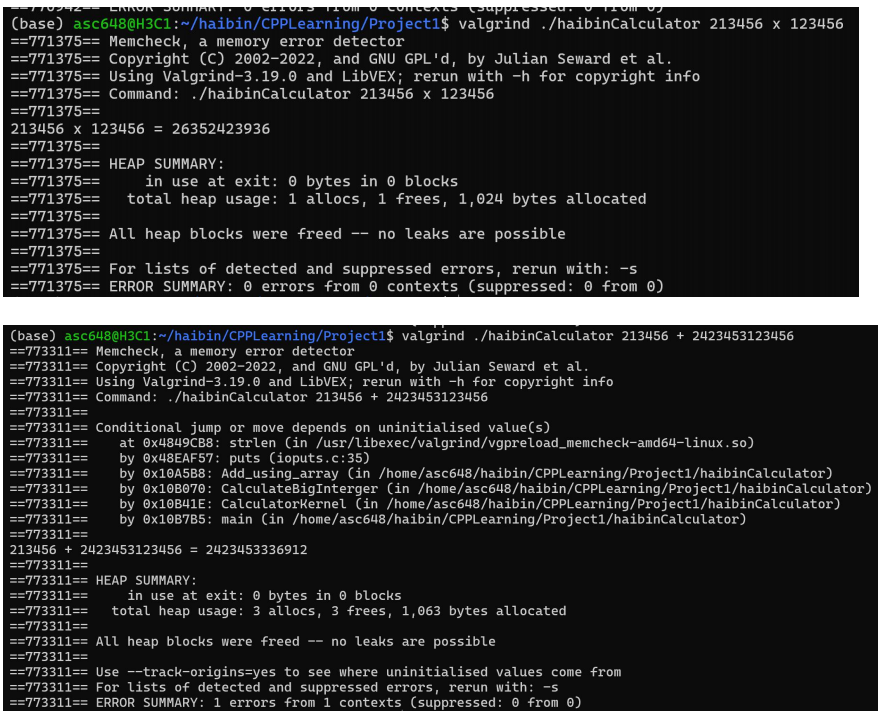
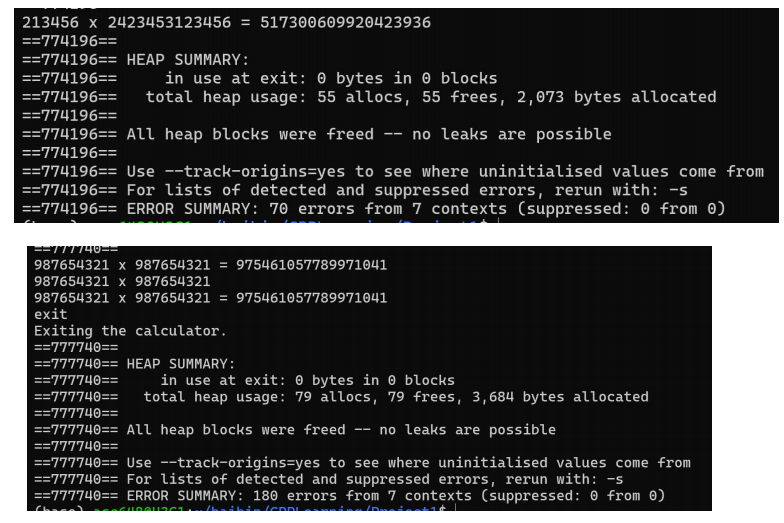
当然,就算是内存泄露了,也没什么问题,我们用 htop 查看我们的计算器占用内存,发现它的占用非常之少,我们可以不管这个内存的泄露。
Part 6: 并行计算
6.1 应用 OpenMP
我简单使用了一下 OpenMp 来完成乘法的并行化。在这里,我学习了 omp 的基本语法。
omp parallel for: 这段 for 循环可以在多核上并行完成
shared: 在循环时,本质上每个核会自己有一份参数的 copy。那么为了保证 copy 的一致性,我们就要将它们设为 shared。其实按照道理 default 状态下 result 和 carry 就都是共享状态了。如果想要每个 for 循环的参数都是独立的,我们要加 private。
reduction: 规约。我们的计算当中,如果想汇总各个计算核心的结果,我们就要加一个reduction 操作。
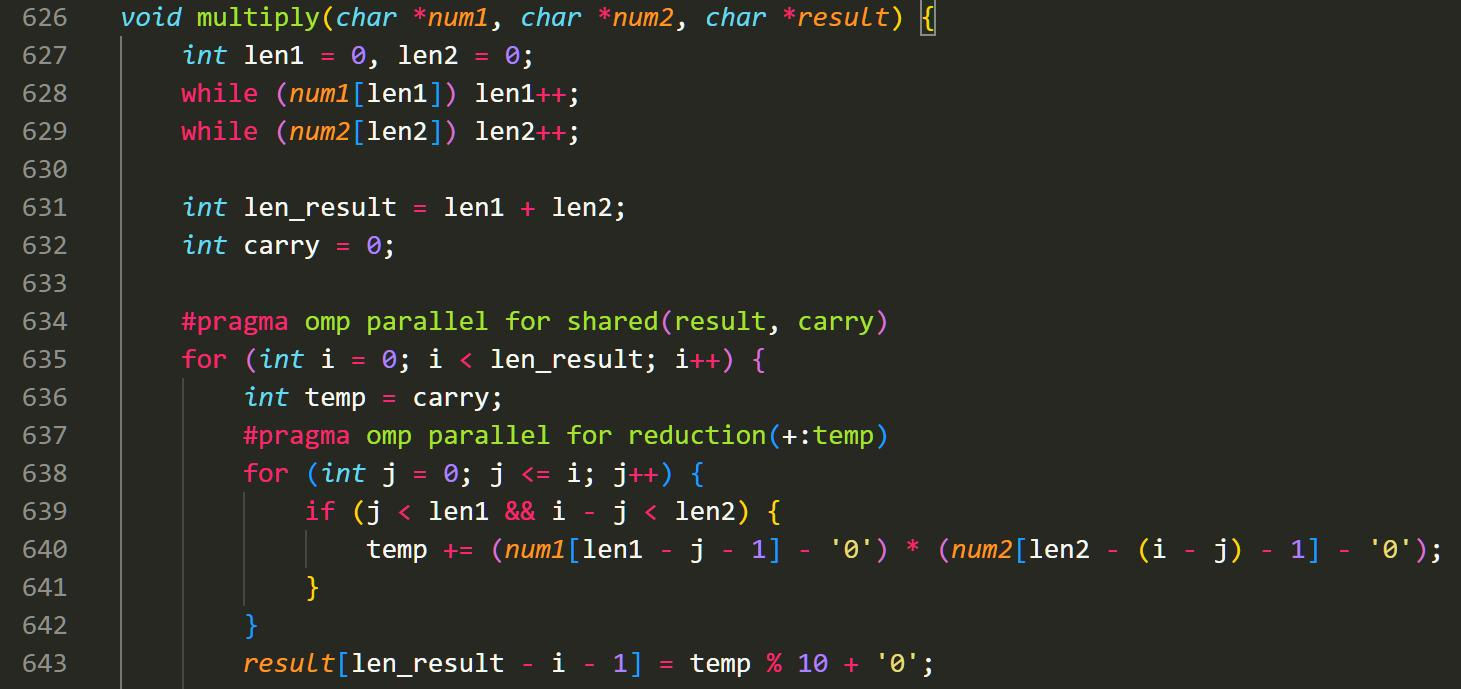
6.2 GPU 编程:将浮点计算移植到 CUDA 架构
在 CUDA 编程中,我们的计算器主要包含两个部分:CPU 上的函数和 GPU 的核函数。GPU 的核函数用 global 表示入口,然后在内部写下函数。只要满足 A = B + C*D 这种矩阵形式,nvcc 在编译时将自动把算法分配到各个核中去执行。
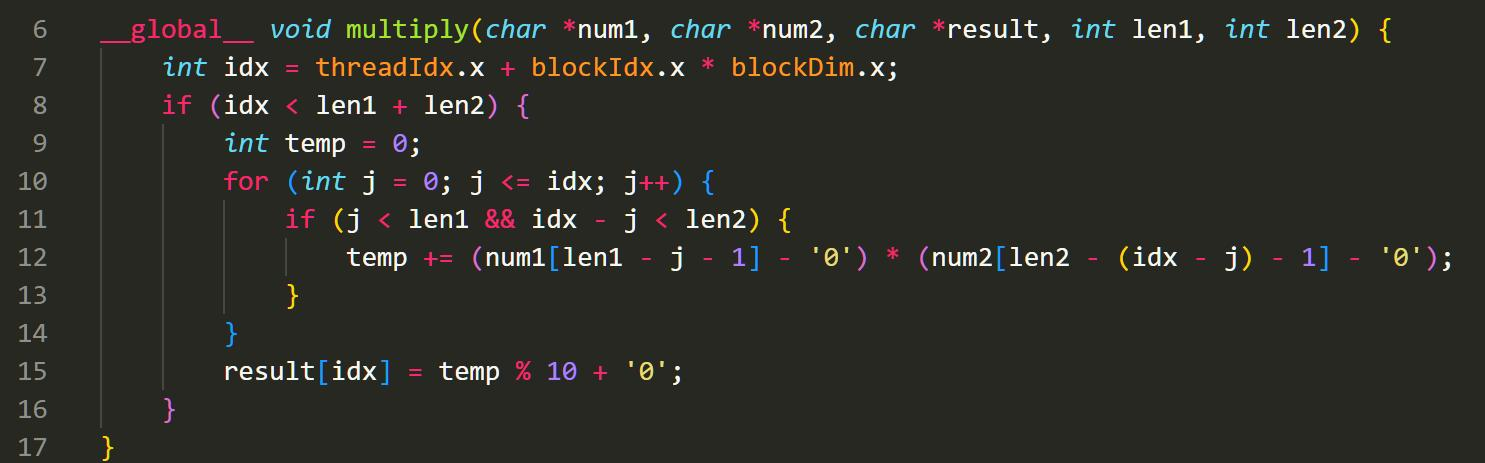
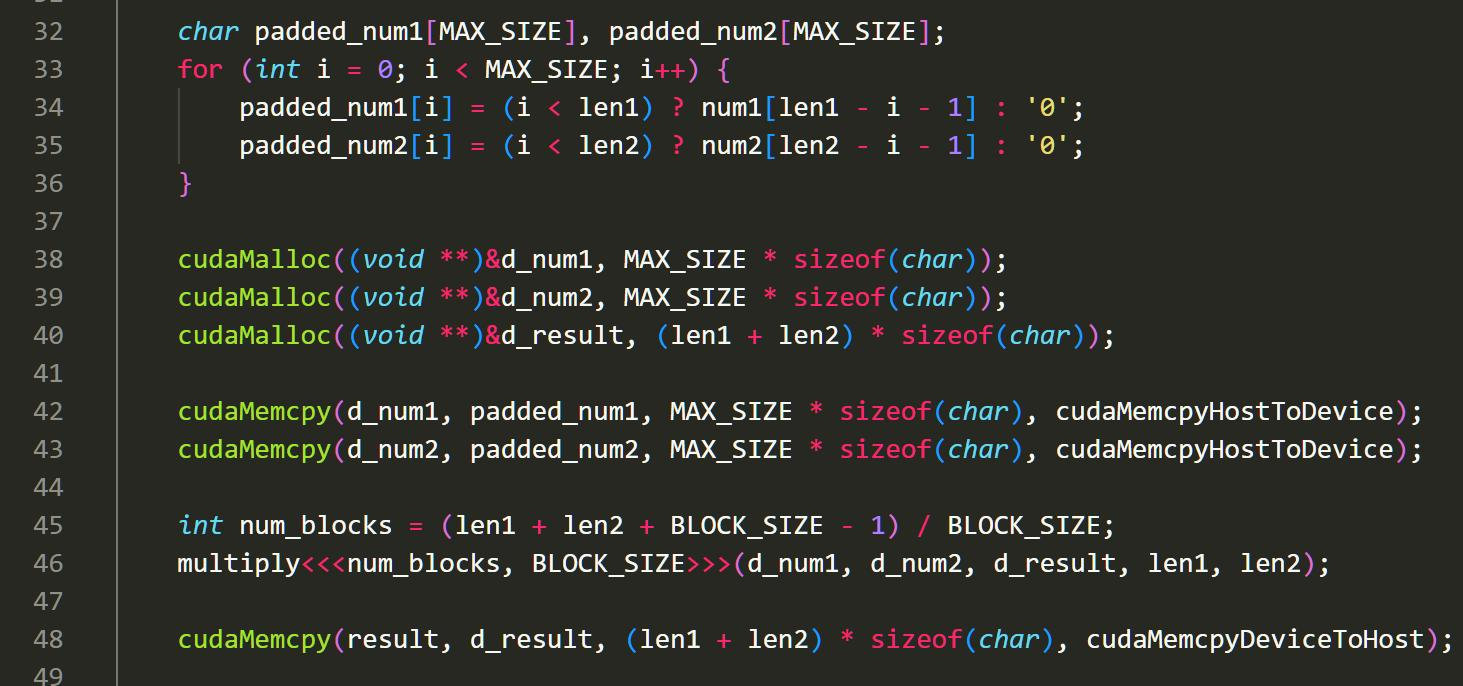
而此时 CPU 由于计算的任务主要有 CUDA 负责了,CPU 任务主要就是将我们的参数搬运到 GPU 的内存中去。我们用 cudaMalloc 函数就能完成了。之后,我们再用 NVCC 编译器去编译我们的 haibinCalculator.cu 文件,就能获得我们的大整数乘法计算器了。
nvcc -o GPUCalculator src/haibin_calculator_cuda.cu
Part 7: Project中的发现
7.1 快速平方根算法背后的秘密
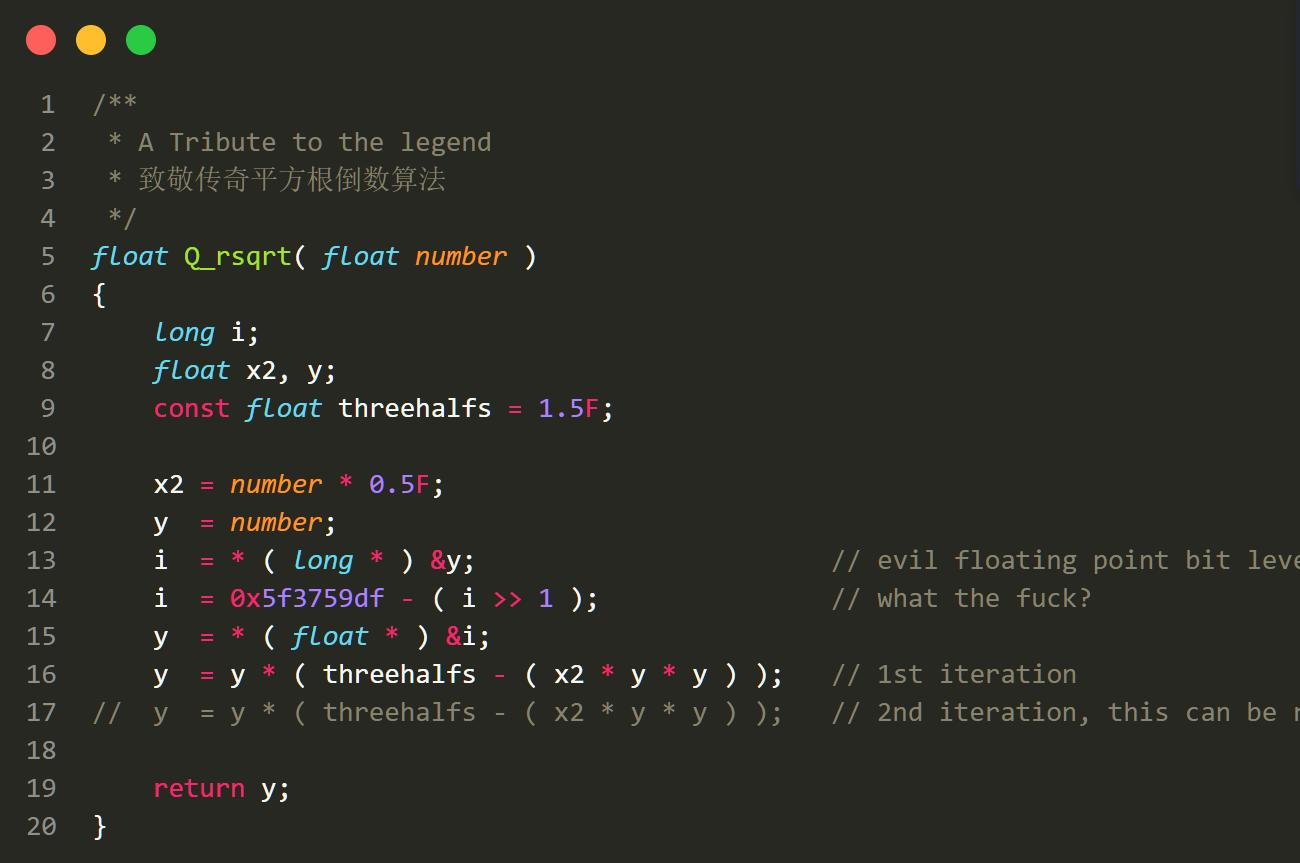
这个算法是一种快速计算浮点数倒数平方根的近似方法,通常被称为"快速平方根"算法。它的起源可以追溯到 Quake III Arena 游戏的源代码,由程序员 John Carmack 在 1999年设计。这个算法以其非常高的性能和相对简单的实现而闻名。
其核心操作为,取出浮点数进行操作,随后使用y=x+b对平方根函数进行近似求解,之后使用牛顿迭代法逼近。
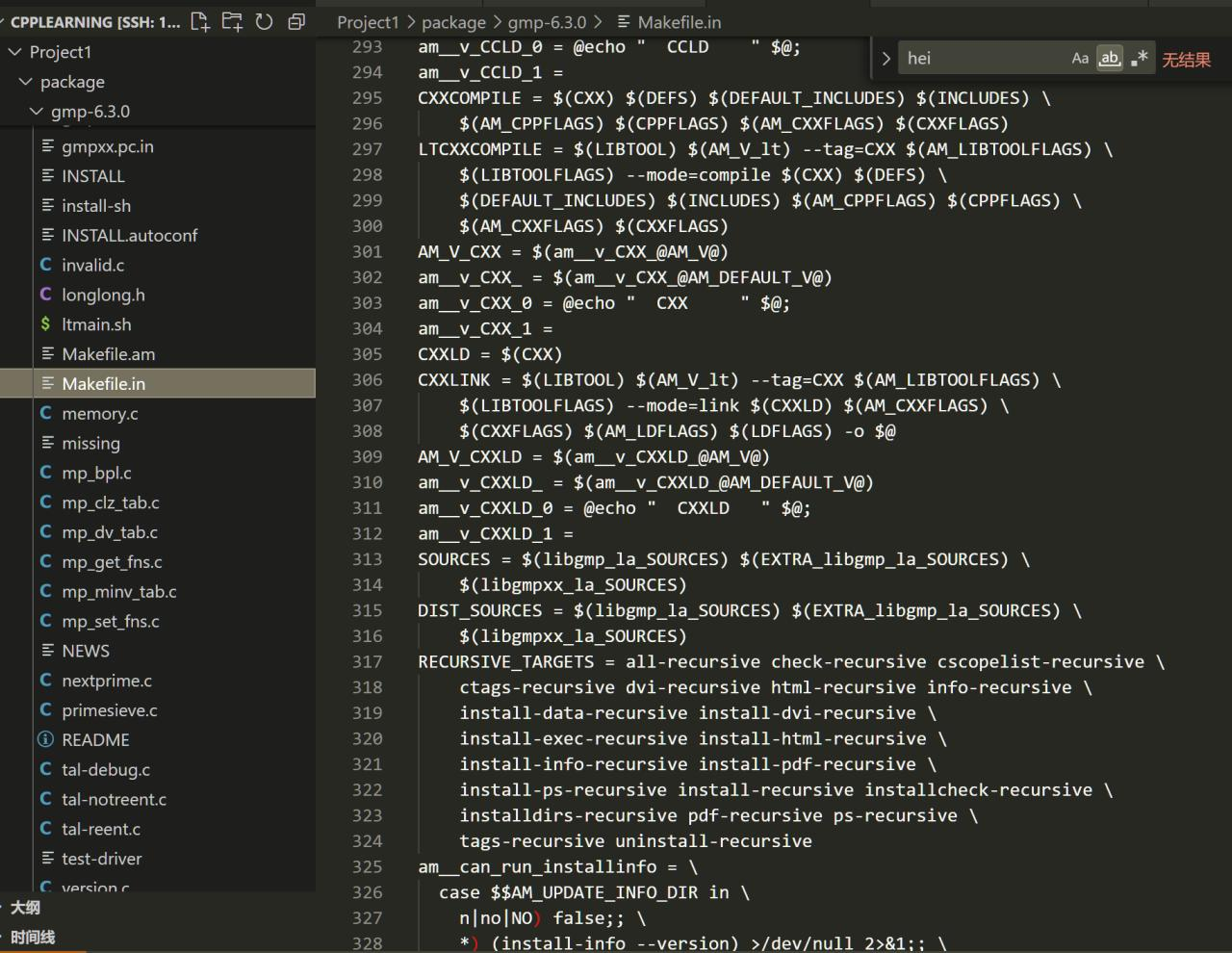
7.2 大整数乘法 GMP 数学库
GMP 大数库是 GUN 项目的一部分,它诞生于 1991 年,作为一个任意精度的大整数运算库,它包含了任意精度的整数、浮点数的各种基础运算操作。它是一个 C 语言库,主要应用于密码学应用和研究、互联网安全应用、代数系统、计算代数研究等。
GMP 库运行速度非常快,有网友测试它算 1000!结果不到一秒钟就已经算好,这还包括了输入输出的时间。
GMP 非常的恐怖,里边的历史日志真的从 1991 年开始记录,一直记录到 2023 年。单单是编译安装我都用了 5 分钟,而里边几百上千个文件,就连 Makefile 都有快千行。我又想到,我的计算器比起 Postgresql 已经是小巫见大巫,而这个 GMP 库的计算器又让 Postgresql显得何其渺小。
结语
这个简单的计算器,让我感受到 C 语言的不简单。虽然才刚刚开始上手,但是指针,内存管理,多线程,优化等等东西都让我感受到这门语言独有的魅力。我认为语言的学习不是学个语法和单词就结束的,也不是学到分支、循环就结束了。学一门语言,就要学它的优势之处,学它的核心要义,这才是最重要的。
而我的这次体验,让我感受到 C 的基础与重要性。我们现在的各种工具,操作系统,最底层里原来也就是这么简单的事务组合而成。想到这里,我又冒出了那个熟悉的词汇:敬畏。这些代码一点一点的累加,才有了今天的高楼大厦。
另外,这次我的研究其实涉及的范围挺广的,主要是因为我单纯抱着第一步认识的兴趣去研究。为什么我想研究这些?其实也没有什么特别的原因。但是我此时想起了朱光潜《谈美》里的一段话:
“科学和哲学穷到极境,都是要满足求知的欲望。每个哲学家和科学家对于他自己所见到的一点真理(无论它究竟是不是真理)都觉得有趣味,都用一股热忱去欣赏它。“地球绕日运行”,“勾方加股方等于弦方”一类的科学事实,和《密罗斯爱神》或《第九交响曲》一样可以摄魂震魄。科学家去寻求这一类的事实,穷到究竟,也正因为它们可以摄魂震魄。所以科学的活动也还是一种艺术的活动,不但善与美是一体,真与美也并没有隔阂。”
写 C 程序的美感跟 Java 很不一样,但是,我很喜欢。
Acknowledgement
感谢肖翊成、马国恒、杨宇坤同学对本次project的支持。
Reference
[1] PostgreSQL Global Development Group. (2024.3). PostgreSQL: Documentation: Main Page. Retrieved from https://doxygen.postgresql.org/
[2] GMP Project. (2023.7). GMP, Arithmetic without limitations: The GNU Multiple Precision
Arithmetic Library. Retrieved from https://gmplib.org/
[3] "IEEE Standard for Binary Floating-Point Arithmetic," in ANSI/IEEE Std 754-1985 , vol., no., pp.1-20, 12 Oct. 1985, doi: 10.1109/IEEESTD.1985.82928. keywords: {Digital
arithmetic;Standards;binary;Floating-point arithmetic},
[4] IEEE Standard 754 for Binary Floating-Point Arithmetic. (1997.10). Retrieved from
https://people.eecs.berkeley.edu/~wkahan/ieee754status/IEEE754.PDF
[5] Burger, Robert G. and R. Kent Dybvig. “ Printing floating-point numbers quickly and
accurately. ” ACM-SIGPLAN Symposium on Programming Language Design and
Implementation (1996).
[6] CUDA C Programming Guide. Retrived from
https://docs.nvidia.cn/cuda/cuda-c-programming-guide/contents.html
[7] Using OpenMP with C. Retrived from
https://curc.readthedocs.io/en/latest/programming/OpenMP-C.html

I used to be able to find good advice from your articles. http://Boyarka-Inform.com/