现在位置: 首页 / 编译原理 / CFG / 正文

Compiler 4: CFG, Parsing

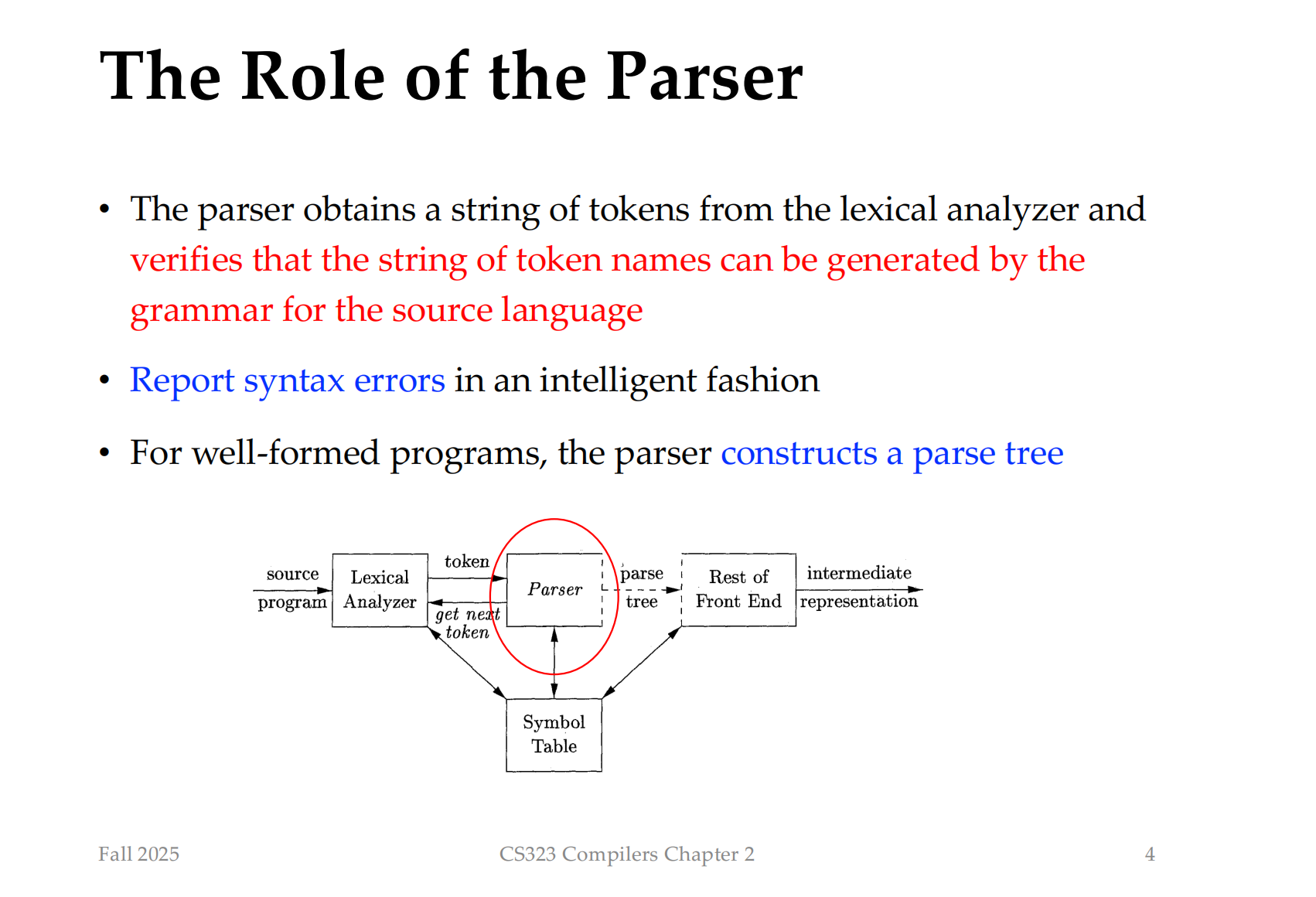
image.png

CFG

image.png

image.png

Terminal: 对应loop，对应if，对应XX

Productions: 产生式

Derivation推导
CFG可以推导很多不同的式子

Notations

Terminologies 文法的句型

这里我们看到，文法

image.png

最左推导 & 最右推导

在编译原理中，最左推导和最右推导都是从文法的开始符号（Start Symbol）出发，通过不断用产生式替换非终结符，逐步推导出一个句子的过程。区别在于：每一步选择替换的非终结符的位置不同。

1. 最左推导（Leftmost Derivation）

  • 规则：在句子中，始终优先替换最左边的非终结符。
  • 意义：生成的过程是“从左到右”逐步展开非终结符。
  • 形式化记号：用 ⇒_lm 表示。

例子：
文法规则：

S → AB
A → a
B → b

推导字符串 ab 的最左推导：

S ⇒_lm AB
  ⇒_lm aB     （替换最左边的非终结符 A）
  ⇒_lm ab     （替换 B）

2. 最右推导（Rightmost Derivation）

  • 规则：在句子中，始终优先替换最右边的非终结符。
  • 意义：生成的过程是“从右到左”逐步展开非终结符。
  • 形式化记号：用 ⇒_rm 表示。

例子：
还是上面的文法，推导字符串 ab 的最右推导：

S ⇒_rm AB
  ⇒_rm Ab     （替换最右边的非终结符 B）
  ⇒_rm ab     （替换 A）

3. 区别与联系

  • 区别：
    • 最左推导：每一步替换最左边的非终结符。
    • 最右推导：每一步替换最右边的非终结符。
  • 联系：
    • 它们推导出的终结串（最终结果）是相同的，只不过推导过程不同。
    • 最左推导对应自顶向下的分析（Top-Down Parsing），常用于递归下降分析。
    • 最右推导的逆过程对应自底向上的分析（Bottom-Up Parsing），尤其是LR分析。

image.png

推导跟分析树是many - one
但是 leftmost / rightmost 跟分析树是 one to one

image.png

模糊的二义性 Ambiguity

如果一个语句，它可以有两个语法分析树，那它就是Ambiguity

image.png

The grammar of a programming language typically needs to be unambiguous

CFGs are more powerful than regexp

CFG are powerful, while regexp are more efficient

Every language that can be described by a regular expression can also be described by a grammar (i.e., every regular language is also a context-free language)

  1. Some context-free languages cannot be described using regular expressions

RegExp = NFA -> CFG 运用构造法证明

Each regular language can be accepted by an NFA. We can construct a CFG to describe the language

对于每个state，我们能做一个nonterminal symbol $A_i$

对于每个跳转/变化，我们能构建 $A_i-> \alpha A_j$

下图里左边是CFG，右边是NFA。

方法：

  1. 根据0，1，2，3，构建：$A_0, A_1, A_2, A_3$
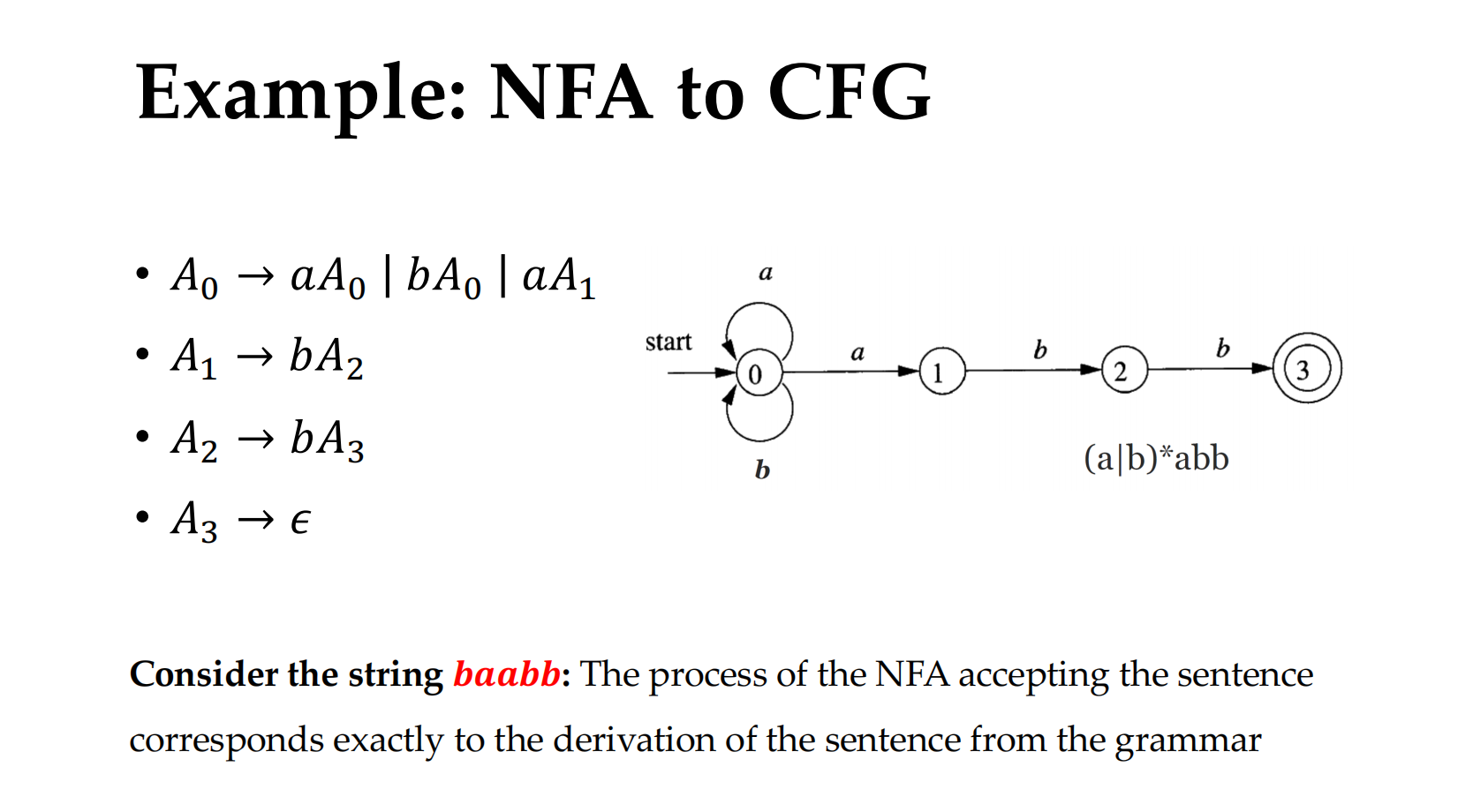
    image.png

So:


Consider the string 𝒃𝒂𝒂𝒃𝒃: The process of the NFA accepting the sentence corresponds exactly to the derivation of the sentence from the grammar

however, CFG > Regular Expression

some Context free languages cannot be described using regulat experssions

ab, aabb, aaabbb，
编程出现：小括号大括号的匹配

你给的文法是：

$$[
S \to aSb \mid ab
]$$

我们来逐步解释它“在说什么”。

1. 推导规律

  • 递归规则：S -> aSb
    表示在一个已经符合规则的串外面，再加一个 a 在最左边、一个 b 在最右边。
  • 基础规则：S -> ab
    表示最基本的串是 "ab"。

2. 能生成的串

从最小的情况出发：

  • S -> ab
  • S -> aSb -> a (ab) b = aabb
  • S -> aSb -> a(aSb)b = aaabb b = aaabbb
  • S -> aSb -> a(a(a b b) b) ... 依次类推

所以生成的串是：

ab, aabb, aaabbb, aaaabbbb, ...

3. 总结规律

这个 CFG 生成的语言是：
$$[
L = { a^n b^n ;\mid; n \geq 1 }
]$$

也就是说：数量相等的 a 和 b，先全是 a，再全是 b。
它表达的是“左右对称、个数匹配”的一种结构。

要不要我帮你画出这个文法的推导树（比如 aaabbb 的最左推导和推导树）
左推导

S
⇒ a S b
⇒ a a S b b
⇒ a a a b b b      （把最左侧的 S 用 ab 代换）
⇒ aaabbb

Parse Tree

S
├── a
├── S
│   ├── a
│   ├── S
│   │   ├── a
│   │   └── b
│   └── b
└── b

image.png
如何证明找不到这个语言？反证法

假设我找到了：

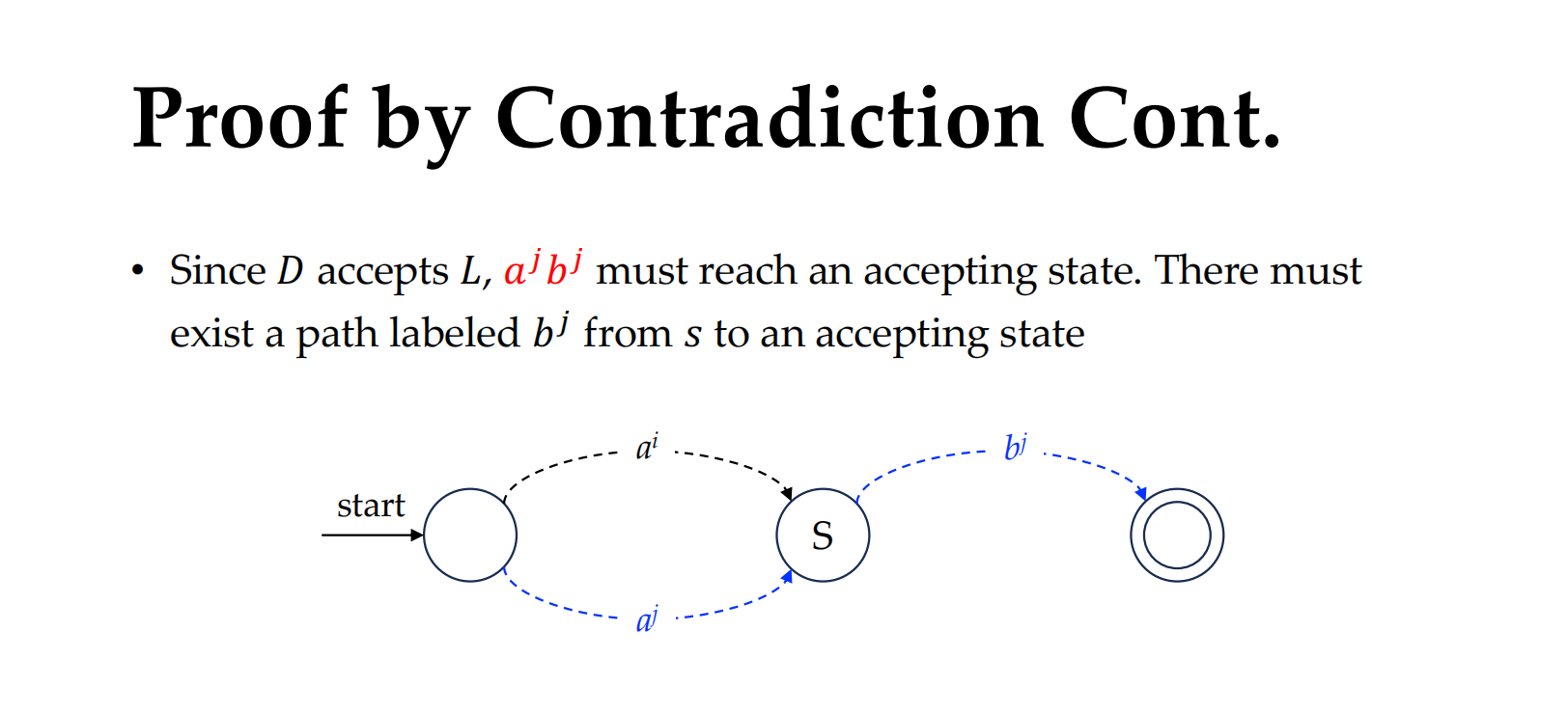
我们中间有一个状态，它是一定会被匹配两次的，分别是字符串 a_i 和 a_j （为什么会被匹配两次呢，因为状态数）

设语言 LLL 是正则的，那么必然存在一个确定有限自动机 (DFA) D 来识别它。
这个 DFA 有 k 个状态。

  1. 处理长串时的状态重复

考虑一个输入串，比如 $s=a^{k+1} b^{k+1} ∈L$。（其实我们可以取 K+2，K+3，K+XXXX状态， 都没关系，说白了就是有限自动机无法表示无限的状态）

  • 当 DFA 读入前 k+1 个 a 的时候，它总共会“走” k+1 步。
  • 但 DFA 只有 k 个状态。

  • 根据鸽巢原理，在这 k+1 步里，必然有两个时刻落在同一个状态。

    • 比如读完前 i 个 a 和读完前 j 个 a（i<j）都到达了状态 s。

形式语言理论里有一个工具叫 抽取引理（Pumping Lemma for Regular Languages），用它能证明 a^n b^n 不是正规语言：

  • 假设 a^n b^n 是正则的。
  • 根据抽取引理，可以把一个足够长的串（比如 a^p b^p）分成三段 xyz，其中中间的 y 可以抽取（重复任意次）而仍然属于语言。
  • 但如果 y 只包含 a，那么多抽几次就会变成 a^(p+|y|) b^p，a 和 b 数量不再相等 → 矛盾。
  • 所以 a^n b^n 不是正则语言。

image.png

那么我们就能匹配上 a_i b_j，但是这不是正则表达式想要的

image.png

Top-Down Parsing

Problem definition: Constructing a parse tree for the input string, starting from the root and creating the nodes of the parse tree in preorder (depth-first)

要根据输入的string，构建一个语法生成树

Two basic actions in top-down parsing:
§ Predict: Determine the production to be applied for the leftmost nonterminal* (of the current parse tree’s frontier)
§ Match: Match the leading terminals in the chosen production’s body with the input string

image.png

Parsing 例子：

用几个语法Grammar Symbol，我们就能匹配 input string

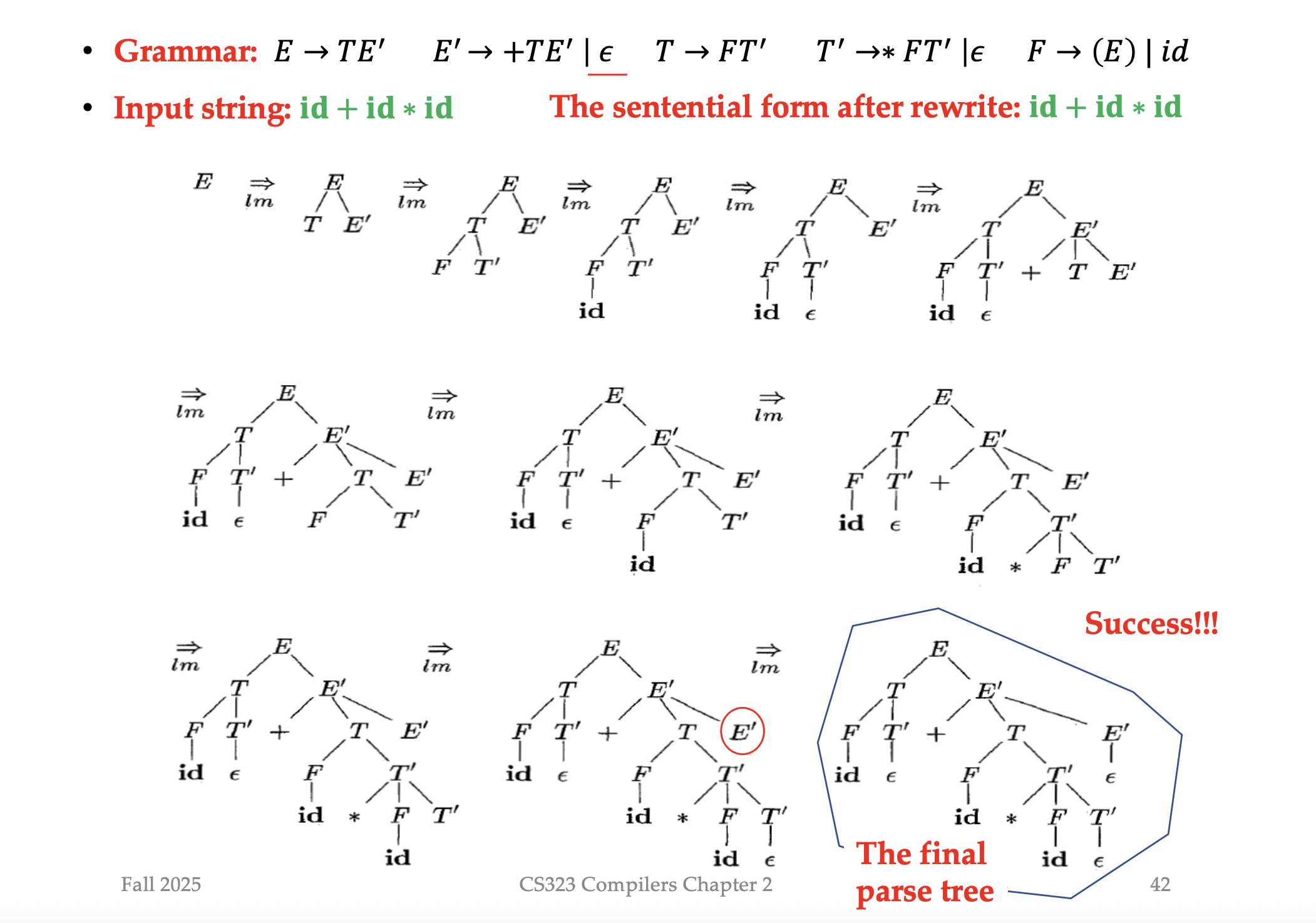
image.png

永远是一个最左的句型（最左推导：每一步替换最左边的非终结符。）
We can make two observations from the example:
• Top-down parsing is equivalent to finding a leftmost derivation.
• At each step, the frontier of the tree is a left-sentential form.

问题：你怎么知道选谁？

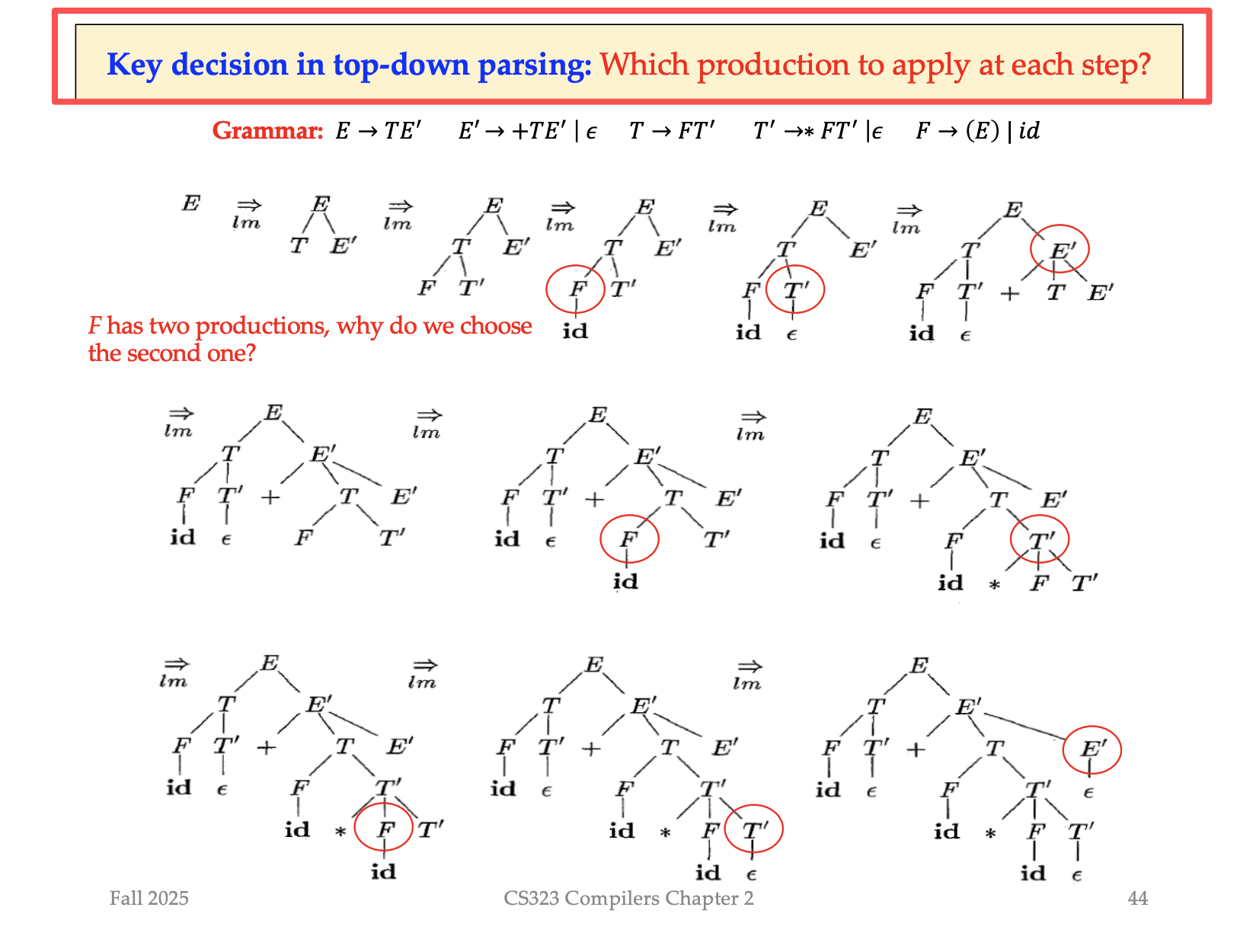
image.png

方法：Recursive-descent parsing

image.png

搜索方法：

  1. 选择一种 A-production 分解方法，将 A分解为 X_1, X_2, ... X_k
  2. 每个X分别的去处理
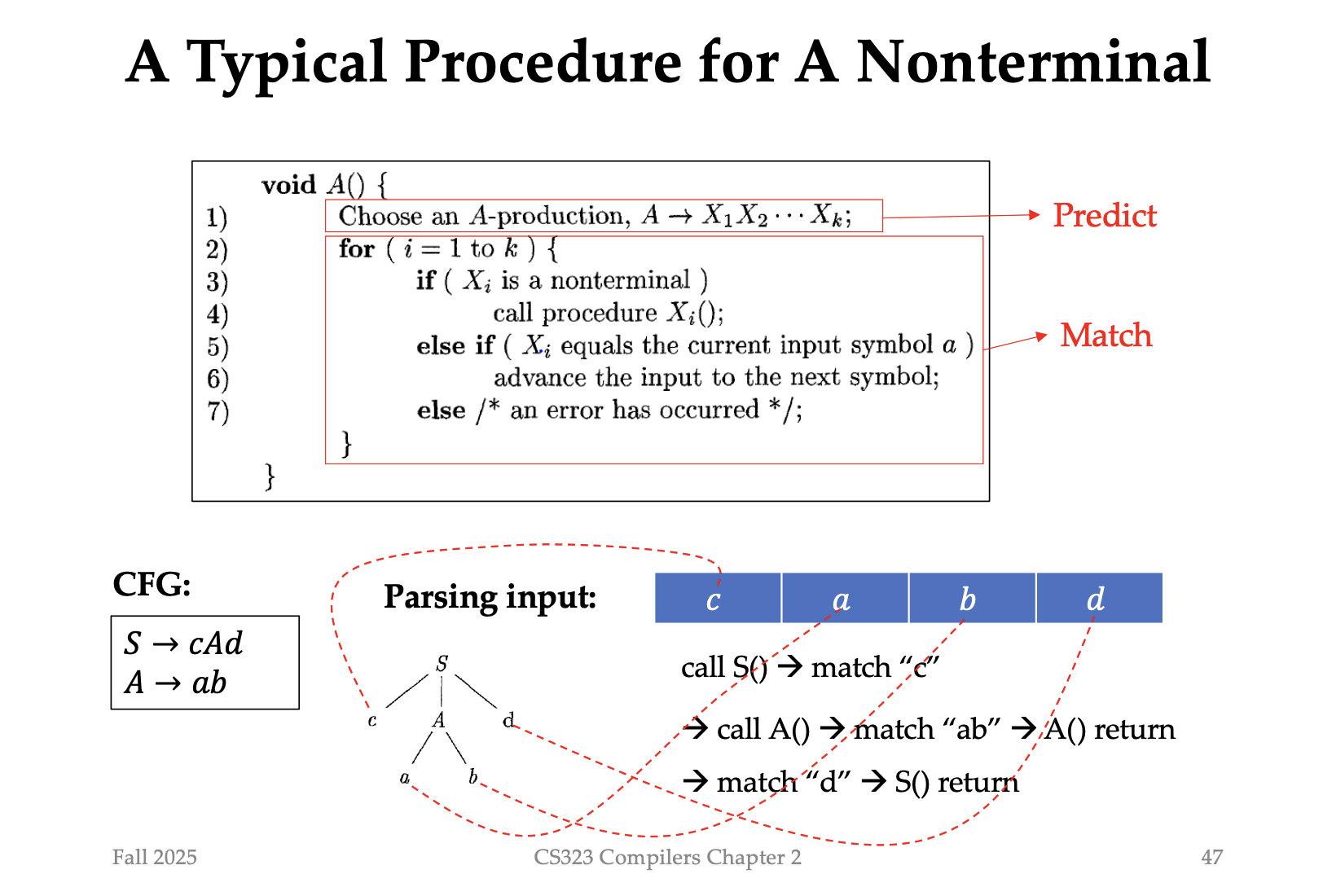
    image.png
    例子：
    A. 先选S，我们选择 S->cAd
    for (c,a,b,d):
    call S() -> match "c"，c是一个terminal
    下一步循环，找到“A”，A不是nonterminal，call A() —— for（a,b） match -> return
    match "d" -> S() return

递归下降：
递归，有可能调用到自己
下降：不断的调方法分解