已弃坑:oneDNN架构解读
- 框架赏析
- 2025-06-17
- 231热度
- 0评论
PS:这玩意已经不更新了,intel 放弃了哈哈哈哈哈哈哈。
https://zhuanlan.zhihu.com/p/20510564015

oneDNN是Intel开源的深度学习加速库,其前身为MKLDNN,对于Intel自家硬件(CPU以及GPU),oneDNN对神经网络算子的计算过程进行了针对性的优化处理,从而显著提升了神经网络算子在Intel硬件下的计算速度。在训练侧,oneDNN已作为第三方工具被目前几乎所有的主流训练框架(TensorFlow、PyTorch、MXNet等)集成;在推理侧,其是OpenVINO的后端,并也经常作为第三方推理加速库被其它工程调用。
学习链接
github
uxlfoundation/oneDNN: oneAPI Deep Neural Network Library (oneDNN)
开发手册
oneAPI Deep Neural Network Library (oneDNN) Developer Guide and Reference — oneDNN v3.9.0 documentation
- oneDNN Developer Guide and Reference explains the programming model, supported functionality, implementation details, and includes annotated examples.
- API Reference provides a comprehensive reference of the library API.
- Release Notes explains the new features, performance optimizations, and improvements implemented in each version of oneDNN.
一些资料
Intel® oneAPI Deep Neural Network Library Documentation
基于oneDNN的ResNet50推理速度优化 - 知乎
在 x86-64 机器上使用 oneDNN Graph 加速推理 | PyTorch - PyTorch 深度学习库
编译搭建
参照Build from Source — oneDNN v3.9.0 documentation
git clone https://github.com/uxlfoundation/oneDNN.git
cd oneDNN
cd build && cmake ..
cmake --build .在编译后你可以在 oneDNN/build/examples 里找到对应的可执行文件。
start from example
oneDNN/examples/tutorials/matmul/cpu_sgemm_and_matmul.cpp at main · uxlfoundation/oneDNN
对应的可执行文件在 oneDNN/build/examples 底下的 cpu-tutorials-matmul-sgemm-and-matmul-cpp
intel的文本是又臭又长,还找不到下手的点。我们还是一样,从例子开始。
我们从sgemm开始学习。
void init_vector(std::vector<float> &v) {
std::mt19937 gen;
std::uniform_real_distribution<float> u(-1, 1);
for (auto &e : v)
e = u(gen);
}
void sgemm_and_matmul_with_params(char transA, char transB, int64_t M,
int64_t N, int64_t K, float alpha, float beta) {
if (beta != fixed_beta)
throw std::logic_error("Run-time beta is not yet supported.");
// Allocate and initialize matrices
std::vector<float> A(M * K);
init_vector(A); // 初始化矩阵A
std::vector<float> B(K * N);
init_vector(B); // 初始化矩阵B
std::vector<float> C_sgemm(M * N);
init_vector(C_sgemm); // 初始化矩阵C
std::vector<float> C_dynamic_matmul = C_sgemm;
// Prepare leading dimensions
int64_t lda = tolower(transA) == 'n' ? K : M;
int64_t ldb = tolower(transB) == 'n' ? N : K;
int64_t ldc = N;
// 1. Execute sgemm
for (int run = 0; run < number_of_runs; ++run)
dnnl_sgemm(transA, transB, M, N, K, alpha, A.data(), lda, B.data(), ldb,
beta, C_sgemm.data(), ldc);
// 2.a Create dynamic MatMul
auto dynamic_matmul = dynamic_matmul_create();
// 2.b Execute
for (int run = 0; run < number_of_runs; ++run)
dynamic_matmul_execute(dynamic_matmul, transA, transB, M, N, K, alpha,
A.data(), lda, B.data(), ldb, beta, C_dynamic_matmul.data(),
ldc);
int rc = 0;
rc |= compare_vectors(
C_sgemm, C_dynamic_matmul, K, "Compare SGEMM vs dynamic MatMul");
if (rc) throw std::logic_error("The resulting matrices diverged too much.");
}
void sgemm_and_matmul() {
sgemm_and_matmul_with_params('N', 'T', 10, 20, 30, 1.1f, fixed_beta);
}
int main(int argc, char **argv) {
return handle_example_errors({engine::kind::cpu}, sgemm_and_matmul);
}我们先看 dnnl_sgemm(transA, transB, M, N, K, alpha, A.data(), lda, B.data(), ldb, beta, C_sgemm.data(), ldc);
oneDNN/src/common/gemm.cpp at 9136964f8cc9e9c8a3ef4e3d38eee1baff68ccc4 · uxlfoundation/oneDNN
dnnl_status_t dnnl_sgemm(char transa, char transb, dim_t M, dim_t N, dim_t K,
float alpha, const float *A, dim_t lda, const float *B, const dim_t ldb,
float beta, float *C, dim_t ldc) {
#if DNNL_CPU_RUNTIME != DNNL_RUNTIME_NONE
status_t status = dnnl_success;
MAYBE_VERBOSE(status, "f32", "f32", "f32",
MAYBE_RUN_STACK_CHECKER(dnnl_sgemm, cpu::extended_sgemm, &transb,
&transa, &N, &M, &K, &alpha, B, &ldb, A, &lda, &beta, C,
&ldc, nullptr, false));
return status;
#else
return dnnl::impl::status::unimplemented;
#endif
}它会调用 cpu::extended_sgemm,在 oneDNN/src/cpu/gemm/gemm.cpp at 9136964f8cc9e9c8a3ef4e3d38eee1baff68ccc4 · uxlfoundation/oneDNN
dnnl_status_t extended_sgemm(const char *transa, const char *transb,
const dim_t *M, const dim_t *N, const dim_t *K, const float *alpha,
const float *A, const dim_t *lda, const float *B, const dim_t *ldb,
const float *beta, float *C, const dim_t *ldc, const float *bias,
const bool force_jit_nocopy_gemm) {
dnnl_status_t status = check_gemm_input(transa, transb, M, N, K, A, lda, B,
ldb, C, ldc, alpha, beta, bias != nullptr);
if (status != dnnl_success) return status;
#ifdef USE_CBLAS
if (!force_jit_nocopy_gemm && utils::one_of(*transa, 'n', 'N', 't', 'T')
&& utils::one_of(*transb, 'n', 'N', 't', 'T')) {
bool trA = *transa == 't' || *transa == 'T';
bool trB = *transb == 't' || *transb == 'T';
CBLAS_TRANSPOSE Cblas_trA = trA ? CblasTrans : CblasNoTrans;
CBLAS_TRANSPOSE Cblas_trB = trB ? CblasTrans : CblasNoTrans;
cblas_sgemm(CblasColMajor, Cblas_trA, Cblas_trB, *M, *N, *K, *alpha, A,
*lda, B, *ldb, *beta, C, *ldc);
if (bias) {
// Add bias if necessary (bias is applied to columns of C)
dim_t incx = 1, incy = 1;
parallel_nd(*N, [&](dim_t n) {
dim_t offset = n * (*ldc);
cblas_saxpy(*M, 1.0, bias, incx, C + offset, incy);
});
}
msan_unpoison_matrix(C, *M, *N, *ldc, sizeof(*C));
return dnnl_success;
}
#endif
#if DNNL_X64 && !__BUILD_GEMM_NONE
if (mayiuse(sse41)) {
float *dummy_ao = nullptr;
float *dummy_bo = nullptr;
auto status = gemm_driver(transa, transb, bias ? "C" : nullptr, M, N, K,
alpha, A, lda, dummy_ao, B, ldb, dummy_bo, beta, C, ldc, bias,
force_jit_nocopy_gemm);
if (status != status::unimplemented) return status;
}
#endif
return ref_gemm<float>(
transa, transb, M, N, K, alpha, A, lda, B, ldb, beta, C, ldc, bias);
}怎么在用cblas .......
那我们对比的呢:
// 2.a Create dynamic MatMul
auto dynamic_matmul = dynamic_matmul_create();
// 2.b Execute
for (int run = 0; run < number_of_runs; ++run)
dynamic_matmul_execute(dynamic_matmul, transA, transB, M, N, K, alpha,
A.data(), lda, B.data(), ldb, beta, C_dynamic_matmul.data(),
ldc);// Create a _dynamic_ MatMul primitive that can work with arbitrary shapes
// and alpha parameters.
// Warning: current limitation is that beta parameter should be known in
// advance (use fixed_beta).
matmul dynamic_matmul_create() {
// We assume that beta is known at the primitive creation time
float beta = fixed_beta;
memory::dims a_shape = {DNNL_RUNTIME_DIM_VAL, DNNL_RUNTIME_DIM_VAL};
memory::dims b_shape = {DNNL_RUNTIME_DIM_VAL, DNNL_RUNTIME_DIM_VAL};
memory::dims c_shape = {DNNL_RUNTIME_DIM_VAL, DNNL_RUNTIME_DIM_VAL};
memory::dims a_strides = {DNNL_RUNTIME_DIM_VAL, DNNL_RUNTIME_DIM_VAL};
memory::dims b_strides = {DNNL_RUNTIME_DIM_VAL, DNNL_RUNTIME_DIM_VAL};
memory::dims c_strides = {DNNL_RUNTIME_DIM_VAL, 1};
memory::desc a_md(a_shape, memory::data_type::f32, a_strides);
memory::desc b_md(b_shape, memory::data_type::f32, b_strides);
memory::desc c_md(c_shape, memory::data_type::f32, c_strides);
// Create attributes (to handle alpha dynamically and beta if necessary)
primitive_attr attr;
attr.set_scales_mask(DNNL_ARG_WEIGHTS, /* mask */ 0);
if (beta != 0.f) {
post_ops po;
po.append_sum(beta);
attr.set_post_ops(po);
}
// Create a MatMul primitive
matmul::primitive_desc matmul_pd(eng(), a_md, b_md, c_md, attr);
return matmul(matmul_pd);
}
// Execute a _dynamic_ MatMul primitive created earlier. All the parameters are
// passed at a run-time (except for beta which has to be specified at the
// primitive creation time due to the current limitation).
void dynamic_matmul_execute(matmul &matmul_p, char transA, char transB,
int64_t M, int64_t N, int64_t K, float alpha, const float *A,
int64_t lda, const float *B, int64_t ldb, float beta, float *C,
int64_t ldc) {
using dims = memory::dims;
if (beta != fixed_beta)
throw std::logic_error("Run-time beta is not yet supported.");
// Translate transA and transB
dims a_strides = tolower(transA) == 'n' ? dims {lda, 1} : dims {1, lda};
dims b_strides = tolower(transB) == 'n' ? dims {ldb, 1} : dims {1, ldb};
// Wrap raw pointers into oneDNN memories (with proper shapes)
memory A_m({{M, K}, memory::data_type::f32, a_strides}, eng(), (void *)A);
memory B_m({{K, N}, memory::data_type::f32, b_strides}, eng(), (void *)B);
memory C_m({{M, N}, memory::data_type::f32, {ldc, 1}}, eng(), (void *)C);
// Prepare oneDNN memory for alpha
memory alpha_m({{1}, memory::data_type::f32, {1}}, eng(), &alpha);
// Execute the MatMul primitive
stream s(eng());
matmul_p.execute(s,
{{DNNL_ARG_SRC, A_m}, {DNNL_ARG_WEIGHTS, B_m}, {DNNL_ARG_DST, C_m},
{DNNL_ARG_ATTR_SCALES | DNNL_ARG_WEIGHTS, alpha_m}});
s.wait();
}
| 实现点 | 技术细节 |
|---|---|
| 动态 shape | 使用 DNNL_RUNTIME_DIM_VAL 占位,实际 shape 在 memory 创建时提供 |
| 动态 alpha | 使用 set_scales_mask() + runtime alpha_m memory |
| beta | 只能固定在 primitive 创建阶段,通过 post_ops.append_sum(beta) 实现 |
| A/B 的转置 | 使用 strides 控制内存布局来间接实现转置 |
| 高效执行 | 创建好 matmul primitive 后可多次执行,避免重复编译 |
| 支持动态 batch | 也可以加上 DNNL_RUNTIME_DIM_VAL, M, K 来支持动态批次矩阵乘法 |
- 缓存多个 primitive 实例
- 比如根据
(transA, transB, beta)组合缓存不同 primitive; - 每次选择对应的 primitive 执行。
- 比如根据
- 构造 higher-level dispatch wrapper
- 手动判断 transpose、beta 等参数;
- 动态创建 memory::desc 和 primitive_attr。
- 用 brgemm(batch-reduce GEMM)自己写 kernel
- 如果你需要更细粒度的动态控制,例如动态 tile、大量 shape 变动等,可以直接使用
brgemm接口自行调度。
- 如果你需要更细粒度的动态控制,例如动态 tile、大量 shape 变动等,可以直接使用
传统DNN kernel
s8x8s32 计算学习
这段代码实现的是 oneDNN 中用于 int8 量化 GEMM 的一项关键计算:compensation 补偿向量的生成。它主要用于:
修正 int8 点积时带来的零点偏移(zero-point offset)误差,尤其是量化 B 矩阵为
int8,而 A 矩阵乘以 B 后结果要校正偏置时。
namespace dnnl {
namespace impl {
namespace cpu {
namespace ppc64 {
dnnl_status_t cblas_gemm_s8x8s32_ppc64(int ATflag, int BTflag,
char const *offsetc, dim_t m, dim_t n, dim_t k, float alpha,
int8_t const *A, dim_t lda, int8_t const *ao, uint8_t const *B,
dim_t ldb, uint8_t const *bo, int *C, float beta, dim_t ldc,
int const *co, int flipB_flag) {
int m_cap, n_cap, k_cap;
m_cap = (m + 3) & (~3);
n_cap = (n + 3) & (~3);
k_cap = (k + 3) & (~3);
if ((*ao != 0) || (*bo != 0)) {
short *Ashort, *AP, *APraw;
short *Bshort, *BP, *BPraw;
int a_size = lda * (ATflag ? m - 1 : k - 1) + (ATflag ? k : m);
int b_size = ldb * (BTflag ? k - 1 : n - 1) + (BTflag ? n : k);
Ashort = (short *)malloc(a_size * sizeof(short), 4096);
Bshort = (short *)malloc(b_size * sizeof(short), 4096);
if (utils::any_null(Ashort, Bshort)) {
free(Ashort);
free(Bshort);
return dnnl_out_of_memory;
}
for (int i = 0; i < a_size; ++i)
Ashort[i] = ((short)A[i]) - (short)*ao;
if (flipB_flag) {
const int8_t *Bflip = (const int8_t *)B;
const int8_t *bo_flip = (const int8_t *)bo;
for (int i = 0; i < b_size; ++i)
Bshort[i] = ((short)(Bflip[i])) - (short)*bo_flip;
} else {
for (int i = 0; i < b_size; ++i)
Bshort[i] = ((short)B[i]) - (short)*bo;
}
APraw = (short *)malloc((m_cap * k_cap + 15) * sizeof(short), 4096);
BPraw = (short *)malloc((k_cap * n_cap + 15) * sizeof(short), 4096);
if (utils::any_null(APraw, BPraw)) {
free(Ashort);
free(Bshort);
free(APraw);
free(BPraw);
return dnnl_out_of_memory;
}
AP = (short *)((((unsigned long)APraw) + 15) & (~15));
BP = (short *)((((unsigned long)BPraw) + 15) & (~15));
if (ATflag)
pack_N16_16bit(k, m, Ashort, lda, AP);
else
pack_T16_16bit(k, m, Ashort, lda, AP);
if (BTflag)
pack_T8_16bit(k, n, Bshort, ldb, BP);
else
pack_N8_16bit(k, n, Bshort, ldb, BP);
gemm_kernel_16bit(m, n, k, (float)alpha, AP, BP, C, beta, ldc);
free(Ashort);
free(Bshort);
free(APraw);
free(BPraw);
} else {
int8_t *AP, *APraw;
uint8_t *BP, *BPraw;
APraw = (int8_t *)malloc((m_cap * k_cap + 3) * sizeof(uint8_t), 4096);
BPraw = (uint8_t *)malloc((k_cap * n_cap + 3) * sizeof(int8_t), 4096);
if (utils::any_null(APraw, BPraw)) {
free(APraw);
free(BPraw);
return dnnl_out_of_memory;
}
AP = (int8_t *)((((unsigned long)APraw) + 3) & (~3));
BP = (uint8_t *)((((unsigned long)BPraw) + 3) & (~3));
if (ATflag)
pack_N16_8bit(k, m, A, lda, AP);
else
pack_T16_8bit(k, m, A, lda, AP);
if (flipB_flag) {
int b_size = ldb * (BTflag ? k - 1 : n - 1) + (BTflag ? n : k);
uint8_t *Bflip = (uint8_t *)malloc(b_size * sizeof(uint8_t), 4096);
if (utils::any_null(Bflip)) {
free(APraw);
free(BPraw);
free(Bflip);
return dnnl_out_of_memory;
}
for (int i = 0; i < b_size; ++i)
Bflip[i] = B[i] ^ 0x80;
if (BTflag)
pack_T8_8bit(k, n, Bflip, ldb, BP);
else
pack_N8_8bit(k, n, Bflip, ldb, BP);
free(Bflip);
} else {
if (BTflag)
pack_T8_8bit(k, n, B, ldb, BP);
else
pack_N8_8bit(k, n, B, ldb, BP);
}
gemm_kernel_8bit(m, n, k, (float)alpha, AP, BP, C, beta, ldc);
if (flipB_flag) {
int *comparray = (int *)malloc(m * sizeof(int), 4096);
if (utils::any_null(comparray)) {
free(APraw);
free(BPraw);
free(comparray);
return dnnl_out_of_memory;
}
for (int i = 0; i < m; ++i)
comparray[i] = 0;
if (ATflag) {
for (int i = 0; i < m; ++i) {
int ca = 0;
const int8_t *at = &A[lda * i];
for (int j = 0; j < k; ++j) {
ca += (int)*at++;
}
comparray[i] = ca;
}
} else {
for (int j = 0; j < k; ++j) {
int *ca = comparray;
const int8_t *at = &A[lda * j];
for (int i = 0; i < m; ++i) {
*ca++ += (int)*at++;
}
}
}
for (int i = 0; i < m; ++i) {
comparray[i] = cpu::q10n::out_round<int32_t>(
cpu::q10n::saturate<int32_t>(
((double)comparray[i]) * alpha * -128.0));
}
for (int j = 0; j < n; ++j) {
int *ca = comparray;
int *ct = &C[ldc * j];
for (int i = 0; i < m; ++i) {
*ct++ += *ca++;
}
}
free(comparray);
}
free(APraw);
free(BPraw);
}
if (*offsetc == 'F' || *offsetc == 'f')
for (int i = 0; i < n; ++i)
for (int j = 0; j < m; ++j)
C[ldc * i + j] += co[0];
if (*offsetc == 'R' || *offsetc == 'r')
for (int i = 0; i < n; ++i)
for (int j = 0; j < m; ++j)
C[ldc * i + j] += co[i];
if (*offsetc == 'C' || *offsetc == 'c')
for (int i = 0; i < n; ++i)
for (int j = 0; j < m; ++j)
C[ldc * i + j] += co[j];
return dnnl_success;
}
} // namespace ppc64
} // namespace cpu
} // namespace impl
} // namespace dnnlgemm_kernel_8bit
| 优化维度 | 具体手段 |
|---|---|
| 量化偏移处理 | 支持 A/B 矩阵的 zero_point 偏移 (ao, bo) |
| 内存对齐优化 | malloc(..., 4096) + 手动 pointer 对齐(16-byte 或 4-byte) |
| 打包(packing) | 手动实现数据 layout 转换(pack_T/N_*bit)提升 cache 局部性 |
| 低精度转高精度 | 将 int8/uint8 转为 int16 再计算,提高精度避免溢出 |
| 缓存补偿计算 | 用 comparray 计算 compensation bias,避免 kernel 中处理 |
| B 矩阵符号翻转 | 用 flipB_flag + Bflip = B ^ 0x80 实现 signed->unsigned trick |
| 通道广播补偿 | 支持 offsetc 里的 row/col/full 偏移广播(co[] 加法) |
优化:
| 类别 | 优化点 | 说明 |
|---|---|---|
| 内存 | 对齐 + 页内分配 | 手动 pointer 对齐提升 SIMD 执行效率 |
| layout | 手动打包 | 避免 kernel 内处理复杂 layout |
| 精度 | int8 -> int16 | 避免溢出/溢精问题 |
| 量化 | zero-point 补偿预处理 | 移出主 kernel 的判断逻辑 |
| 补偿项 | A row sum -128 alpha | 支持 flipB trick 的额外补偿 |
| 广播支持 | offsetc 实现 |
符合 Intel GEMM 偏移格式 |
| 数据翻转 | B ^ 0x80 |
uint8 视作 int8 的 SIMD trick |
超级kernel
oneDNN/src/cpu/ppc64/ppc64_gemm_s8x8s32.hpp at main · uxlfoundation/oneDNN
void gemm_kernel_8bit(dim_t m, dim_t n, dim_t k, float alpha, int8_t *A,
uint8_t *B, int32_t *C, float beta, dim_t ldc) {
int32_t i;
int32_t m_cap = (m + 3) & ~3;
int32_t n_cap = (n + 3) & ~3;
int32_t k_cap = (k + 3) & ~3;
int32_t m_skip;
int32_t n_skip = (n & 8) != (n_cap & 8);
int32_t fastpath;
v4si_t result[4], result_i[4], result_t[4];
vec_t swizA = {0, 1, 2, 3, 16, 17, 18, 19, 4, 5, 6, 7, 20, 21, 22, 23};
vec_t swizB
= {8, 9, 10, 11, 24, 25, 26, 27, 12, 13, 14, 15, 28, 29, 30, 31};
vec_t swizC = {0, 1, 2, 3, 4, 5, 6, 7, 16, 17, 18, 19, 20, 21, 22, 23};
vec_t swizD
= {8, 9, 10, 11, 12, 13, 14, 15, 24, 25, 26, 27, 28, 29, 30, 31};
fastpath = ((alpha == 1.0) && (beta == 0.0));
/* Loop for multiples of 8 */
i = n_cap >> 3;
while (i) {
int32_t j;
int32_t *CO;
int8_t *AO;
CO = C;
C += ldc << 3;
AO = A;
PREFETCH1(A, 128);
PREFETCH1(A, 256);
/* Loop for m >= 16. */
j = m_cap >> 4;
m_skip = (m >> 4) != (m_cap >> 4);
while (j) {
uint8_t *BO = B;
v4si_t *rowC;
__vector_quad acc0, acc1, acc2, acc3, acc4, acc5, acc6, acc7;
SET_ACC_ZERO8();
int32_t l;
vec_t *rowA = (vec_t *)AO;
vec_t *rowB = (vec_t *)BO;
for (l = 0; l < k_cap / 4; l++) {
MMA(&acc0, rowA[0], rowB[0]);
MMA(&acc1, rowA[0], rowB[1]);
MMA(&acc2, rowA[1], rowB[0]);
MMA(&acc3, rowA[1], rowB[1]);
MMA(&acc4, rowA[2], rowB[0]);
MMA(&acc5, rowA[2], rowB[1]);
MMA(&acc6, rowA[3], rowB[0]);
MMA(&acc7, rowA[3], rowB[1]);
rowA += 4;
rowB += 2;
}
if (fastpath) {
SAVE_ACC_ABSC(&acc0, 0);
if ((i == 1) && n_skip) {
SAVE_ACC1_COND_ABSC(&acc1, 0);
} else {
SAVE_ACC1_ABSC(&acc1, 0);
}
CO += 4;
SAVE_ACC_ABSC(&acc2, 0);
if ((i == 1) && n_skip) {
SAVE_ACC1_COND_ABSC(&acc3, 0);
} else {
SAVE_ACC1_ABSC(&acc3, 0);
}
CO += 4;
SAVE_ACC_ABSC(&acc4, 0);
if ((i == 1) && n_skip) {
SAVE_ACC1_COND_ABSC(&acc5, 0);
} else {
SAVE_ACC1_ABSC(&acc5, 0);
}
CO += 4;
if (((j == 1) && m_skip) || ((i == 1) && n_skip)) {
if ((j == 1) && m_skip) {
int32_t count = 4 - (m_cap - m);
int32_t ii;
__builtin_mma_disassemble_acc((void *)result, &acc6);
SWIZZLE_4x4 for (ii = 0; ii < count; ++ii)
CO[0 * ldc + ii]
= result_t[0][ii];
for (ii = 0; ii < count; ++ii)
CO[1 * ldc + ii] = result_t[1][ii];
for (ii = 0; ii < count; ++ii)
CO[2 * ldc + ii] = result_t[2][ii];
for (ii = 0; ii < count; ++ii)
CO[3 * ldc + ii] = result_t[3][ii];
__builtin_mma_disassemble_acc((void *)result, &acc7);
SWIZZLE_4x4 for (ii = 0; ii < count; ++ii)
CO[4 * ldc + ii]
= result_t[0][ii];
if ((i > 1) || (!n_skip) || (n_cap & 4)
|| (n_cap - n) < 3)
for (ii = 0; ii < count; ++ii)
CO[5 * ldc + ii] = result_t[1][ii];
if ((i > 1) || (!n_skip) || (n_cap & 4)
|| (n_cap - n) < 2)
for (ii = 0; ii < count; ++ii)
CO[6 * ldc + ii] = result_t[2][ii];
if ((i > 1) || (!n_skip) || (n_cap & 4)
|| (n_cap - n) < 1)
for (ii = 0; ii < count; ++ii)
CO[7 * ldc + ii] = result_t[3][ii];
} else {
SAVE_ACC_ABSC(&acc6, 0);
SAVE_ACC1_COND_ABSC(&acc7, 0);
}
} else {
SAVE_ACC_ABSC(&acc6, 0);
SAVE_ACC1_ABSC(&acc7, 0);
}
} else {
SAVE_ACC(&acc0, 0);
if ((i == 1) && n_skip) {
SAVE_ACC1_COND(&acc1, 0);
} else {
SAVE_ACC1(&acc1, 0);
}
CO += 4;
SAVE_ACC(&acc2, 0);
if ((i == 1) && n_skip) {
SAVE_ACC1_COND(&acc3, 0);
} else {
SAVE_ACC1(&acc3, 0);
}
CO += 4;
SAVE_ACC(&acc4, 0);
if ((i == 1) && n_skip) {
SAVE_ACC1_COND(&acc5, 0);
} else {
SAVE_ACC1(&acc5, 0);
}
CO += 4;
if (((j == 1) && m_skip) || ((i == 1) && n_skip)) {
if ((j == 1) && m_skip) {
int32_t count = 4 - (m_cap - m);
int32_t ii;
__builtin_mma_disassemble_acc((void *)result, &acc6);
SWIZZLE_4x4 for (ii = 0; ii < count; ++ii)
CO[0 * ldc + ii]
= beta * CO[0 * ldc + ii]
+ alpha * result_t[0][ii];
for (ii = 0; ii < count; ++ii)
CO[1 * ldc + ii] = beta * CO[1 * ldc + ii]
+ alpha * result_t[1][ii];
for (ii = 0; ii < count; ++ii)
CO[2 * ldc + ii] = beta * CO[2 * ldc + ii]
+ alpha * result_t[2][ii];
for (ii = 0; ii < count; ++ii)
CO[3 * ldc + ii] = beta * CO[3 * ldc + ii]
+ alpha * result_t[3][ii];
__builtin_mma_disassemble_acc((void *)result, &acc7);
SWIZZLE_4x4 for (ii = 0; ii < count; ++ii)
CO[4 * ldc + ii]
= beta * CO[4 * ldc + ii]
+ alpha * result_t[0][ii];
if ((i > 1) || (!n_skip) || (n_cap & 4)
|| (n_cap - n) < 3)
for (ii = 0; ii < count; ++ii)
CO[5 * ldc + ii] = beta * CO[5 * ldc + ii]
+ alpha * result_t[1][ii];
if ((i > 1) || (!n_skip) || (n_cap & 4)
|| (n_cap - n) < 2)
for (ii = 0; ii < count; ++ii)
CO[6 * ldc + ii] = beta * CO[6 * ldc + ii]
+ alpha * result_t[2][ii];
if ((i > 1) || (!n_skip) || (n_cap & 4)
|| (n_cap - n) < 1)
for (ii = 0; ii < count; ++ii)
CO[7 * ldc + ii] = beta * CO[7 * ldc + ii]
+ alpha * result_t[3][ii];
} else {
SAVE_ACC(&acc6, 0);
SAVE_ACC1_COND(&acc7, 0);
}
} else {
SAVE_ACC(&acc6, 0);
SAVE_ACC1(&acc7, 0);
}
}
CO += 4;
AO += (k_cap << 4);
BO += (k_cap << 3);
--j;
}
if (m_skip) goto endloop8;
m_skip = (m & 8) != (m_cap & 8);
if (m_cap & 8) {
uint8_t *BO = B;
v4si_t *rowC;
__vector_quad acc0, acc1, acc2, acc3;
SET_ACC_ZERO4();
vec_t *rowA = (vec_t *)AO;
vec_t *rowB = (vec_t *)BO;
int32_t l;
for (l = 0; l < k_cap / 4; l++) {
MMA(&acc0, rowA[0], rowB[0]);
MMA(&acc1, rowA[0], rowB[1]);
MMA(&acc2, rowA[1], rowB[0]);
MMA(&acc3, rowA[1], rowB[1]);
rowA += 2;
rowB += 2;
}
if (fastpath) {
SAVE_ACC_ABSC(&acc0, 0);
if ((i == 1) && n_skip) {
SAVE_ACC1_COND_ABSC(&acc1, 0);
} else {
SAVE_ACC1_ABSC(&acc1, 0);
}
CO += 4;
if (m_skip || ((i == 1) & n_skip)) {
if (m_skip) {
int32_t count = 4 - (m_cap - m);
int32_t ii;
__builtin_mma_disassemble_acc((void *)result, &acc2);
SWIZZLE_4x4 for (ii = 0; ii < count; ++ii)
CO[0 * ldc + ii]
= result_t[0][ii];
for (ii = 0; ii < count; ++ii)
CO[1 * ldc + ii] = result_t[1][ii];
for (ii = 0; ii < count; ++ii)
CO[2 * ldc + ii] = result_t[2][ii];
for (ii = 0; ii < count; ++ii)
CO[3 * ldc + ii] = result_t[3][ii];
__builtin_mma_disassemble_acc((void *)result, &acc3);
SWIZZLE_4x4 for (ii = 0; ii < count; ++ii)
CO[4 * ldc + ii]
= result_t[0][ii];
if ((i > 1) || (!n_skip) || (n_cap & 4)
|| (n_cap - n) < 3)
for (ii = 0; ii < count; ++ii)
CO[5 * ldc + ii] = result_t[1][ii];
if ((i > 1) || (!n_skip) || (n_cap & 4)
|| (n_cap - n) < 2)
for (ii = 0; ii < count; ++ii)
CO[6 * ldc + ii] = result_t[2][ii];
if ((i > 1) || (!n_skip) || (n_cap & 4)
|| (n_cap - n) < 1)
for (ii = 0; ii < count; ++ii)
CO[7 * ldc + ii] = result_t[3][ii];
} else {
SAVE_ACC_ABSC(&acc2, 0);
SAVE_ACC1_COND_ABSC(&acc3, 0);
}
} else {
SAVE_ACC_ABSC(&acc2, 0);
SAVE_ACC1_ABSC(&acc3, 0);
}
} else {
SAVE_ACC(&acc0, 0);
if ((i == 1) && n_skip) {
SAVE_ACC1_COND(&acc1, 0);
} else {
SAVE_ACC1(&acc1, 0);
}
CO += 4;
if (m_skip || ((i == 1) & n_skip)) {
if (m_skip) {
int32_t count = 4 - (m_cap - m);
int32_t ii;
__builtin_mma_disassemble_acc((void *)result, &acc2);
SWIZZLE_4x4 for (ii = 0; ii < count; ++ii)
CO[0 * ldc + ii]
= beta * CO[0 * ldc + ii]
+ alpha * result_t[0][ii];
for (ii = 0; ii < count; ++ii)
CO[1 * ldc + ii] = beta * CO[1 * ldc + ii]
+ alpha * result_t[1][ii];
for (ii = 0; ii < count; ++ii)
CO[2 * ldc + ii] = beta * CO[2 * ldc + ii]
+ alpha * result_t[2][ii];
for (ii = 0; ii < count; ++ii)
CO[3 * ldc + ii] = beta * CO[3 * ldc + ii]
+ alpha * result_t[3][ii];
__builtin_mma_disassemble_acc((void *)result, &acc3);
SWIZZLE_4x4 for (ii = 0; ii < count; ++ii)
CO[4 * ldc + ii]
= beta * CO[4 * ldc + ii]
+ alpha * result_t[0][ii];
if ((i > 1) || (!n_skip) || (n_cap & 4)
|| (n_cap - n) < 3)
for (ii = 0; ii < count; ++ii)
CO[5 * ldc + ii] = beta * CO[5 * ldc + ii]
+ alpha * result_t[1][ii];
if ((i > 1) || (!n_skip) || (n_cap & 4)
|| (n_cap - n) < 2)
for (ii = 0; ii < count; ++ii)
CO[6 * ldc + ii] = beta * CO[6 * ldc + ii]
+ alpha * result_t[2][ii];
if ((i > 1) || (!n_skip) || (n_cap & 4)
|| (n_cap - n) < 1)
for (ii = 0; ii < count; ++ii)
CO[7 * ldc + ii] = beta * CO[7 * ldc + ii]
+ alpha * result_t[3][ii];
} else {
SAVE_ACC(&acc2, 0);
SAVE_ACC1_COND(&acc3, 0);
}
} else {
SAVE_ACC(&acc2, 0);
SAVE_ACC1(&acc3, 0);
}
}
CO += 4;
AO += (k_cap << 3);
BO += (k_cap << 3);
}
if (m_skip) goto endloop8;
m_skip = (m & 4) != (m_cap & 4);
if (m_cap & 4) {
uint8_t *BO = B;
v4si_t *rowC;
__vector_quad acc0, acc1;
__builtin_mma_xxsetaccz(&acc0);
__builtin_mma_xxsetaccz(&acc1);
vec_t *rowA = (vec_t *)AO;
vec_t *rowB = (vec_t *)BO;
int32_t l = 0;
for (l = 0; l < k_cap / 4; l++) {
MMA(&acc0, rowA[0], rowB[0]);
MMA(&acc1, rowA[0], rowB[1]);
rowA += 1;
rowB += 2;
}
if (fastpath) {
if (m_skip || ((i == 1) & n_skip)) {
if (m_skip) {
int32_t count = 4 - (m_cap - m);
int32_t ii;
__builtin_mma_disassemble_acc((void *)result, &acc0);
SWIZZLE_4x4 for (ii = 0; ii < count; ++ii)
CO[0 * ldc + ii]
= result_t[0][ii];
for (ii = 0; ii < count; ++ii)
CO[1 * ldc + ii] = result_t[1][ii];
for (ii = 0; ii < count; ++ii)
CO[2 * ldc + ii] = result_t[2][ii];
for (ii = 0; ii < count; ++ii)
CO[3 * ldc + ii] = result_t[3][ii];
__builtin_mma_disassemble_acc((void *)result, &acc1);
SWIZZLE_4x4 for (ii = 0; ii < count; ++ii)
CO[4 * ldc + ii]
= result_t[0][ii];
if ((i == 1) & n_skip) {
if ((n_cap & 4) || (n_cap - n) < 3)
for (ii = 0; ii < count; ++ii)
CO[5 * ldc + ii] = result_t[1][ii];
if ((n_cap & 4) || (n_cap - n) < 2)
for (ii = 0; ii < count; ++ii)
CO[6 * ldc + ii] = result_t[2][ii];
if ((n_cap & 4) || (n_cap - n) < 1)
for (ii = 0; ii < count; ++ii)
CO[7 * ldc + ii] = result_t[3][ii];
} else {
for (ii = 0; ii < count; ++ii)
CO[5 * ldc + ii] = result_t[1][ii];
for (ii = 0; ii < count; ++ii)
CO[6 * ldc + ii] = result_t[2][ii];
for (ii = 0; ii < count; ++ii)
CO[7 * ldc + ii] = result_t[3][ii];
}
} else {
SAVE_ACC_ABSC(&acc0, 0);
SAVE_ACC1_COND_ABSC(&acc1, 0);
}
} else {
SAVE_ACC_ABSC(&acc0, 0);
SAVE_ACC1_ABSC(&acc1, 0);
}
} else {
if (m_skip || ((i == 1) & n_skip)) {
if (m_skip) {
int32_t count = 4 - (m_cap - m);
int32_t ii;
__builtin_mma_disassemble_acc((void *)result, &acc0);
SWIZZLE_4x4 for (ii = 0; ii < count; ++ii)
CO[0 * ldc + ii]
= beta * CO[0 * ldc + ii]
+ alpha * result_t[0][ii];
for (ii = 0; ii < count; ++ii)
CO[1 * ldc + ii] = beta * CO[1 * ldc + ii]
+ alpha * result_t[1][ii];
for (ii = 0; ii < count; ++ii)
CO[2 * ldc + ii] = beta * CO[2 * ldc + ii]
+ alpha * result_t[2][ii];
for (ii = 0; ii < count; ++ii)
CO[3 * ldc + ii] = beta * CO[3 * ldc + ii]
+ alpha * result_t[3][ii];
__builtin_mma_disassemble_acc((void *)result, &acc1);
SWIZZLE_4x4 for (ii = 0; ii < count; ++ii)
CO[4 * ldc + ii]
= beta * CO[4 * ldc + ii]
+ alpha * result_t[0][ii];
if ((i == 1) & n_skip) {
if ((n_cap & 4) || (n_cap - n) < 3)
for (ii = 0; ii < count; ++ii)
CO[5 * ldc + ii] = beta * CO[5 * ldc + ii]
+ alpha * result_t[1][ii];
if ((n_cap & 4) || (n_cap - n) < 2)
for (ii = 0; ii < count; ++ii)
CO[6 * ldc + ii] = beta * CO[6 * ldc + ii]
+ alpha * result_t[2][ii];
if ((n_cap & 4) || (n_cap - n) < 1)
for (ii = 0; ii < count; ++ii)
CO[7 * ldc + ii] = beta * CO[7 * ldc + ii]
+ alpha * result_t[3][ii];
} else {
for (ii = 0; ii < count; ++ii)
CO[5 * ldc + ii] = beta * CO[5 * ldc + ii]
+ alpha * result_t[1][ii];
for (ii = 0; ii < count; ++ii)
CO[6 * ldc + ii] = beta * CO[6 * ldc + ii]
+ alpha * result_t[2][ii];
for (ii = 0; ii < count; ++ii)
CO[7 * ldc + ii] = beta * CO[7 * ldc + ii]
+ alpha * result_t[3][ii];
}
} else {
SAVE_ACC(&acc0, 0);
SAVE_ACC1_COND(&acc1, 0);
}
} else {
SAVE_ACC(&acc0, 0);
SAVE_ACC1(&acc1, 0);
}
}
CO += 4;
AO += (k_cap << 2);
BO += (k_cap << 3);
}
endloop8:
B += k_cap << 3;
i -= 1;
}
if (n_cap & 4) {
int32_t j;
int32_t *CO;
int8_t *AO;
CO = C;
C += ldc << 2;
AO = A;
int32_t n_skip = (n != n_cap);
/* Loop for m >= 32. */
m_skip = (m >> 5) != (m_cap >> 5);
for (j = 0; j < (m_cap >> 5); j++) {
uint8_t *BO = B;
int8_t *A1 = AO + (16 * k_cap);
v4si_t *rowC;
__vector_quad acc0, acc1, acc2, acc3, acc4, acc5, acc6, acc7;
SET_ACC_ZERO8();
vec_t *rowA = (vec_t *)AO;
vec_t *rowA1 = (vec_t *)A1;
vec_t *rowB = (vec_t *)BO;
int32_t l;
for (l = 0; l < k_cap / 4; l++) {
MMA(&acc0, rowA[0], rowB[0]);
MMA(&acc1, rowA[1], rowB[0]);
MMA(&acc2, rowA[2], rowB[0]);
MMA(&acc3, rowA[3], rowB[0]);
MMA(&acc4, rowA1[0], rowB[0]);
MMA(&acc5, rowA1[1], rowB[0]);
MMA(&acc6, rowA1[2], rowB[0]);
MMA(&acc7, rowA1[3], rowB[0]);
rowA += 4;
rowA1 += 4;
rowB += 1;
}
if (fastpath) {
if (m_skip || n_skip) {
SAVE_ACC_COND_ABSC(&acc0, 0);
SAVE_ACC_COND_ABSC(&acc1, 4);
SAVE_ACC_COND_ABSC(&acc2, 8);
SAVE_ACC_COND_ABSC(&acc3, 12);
SAVE_ACC_COND_ABSC(&acc4, 16);
SAVE_ACC_COND_ABSC(&acc5, 20);
SAVE_ACC_COND_ABSC(&acc6, 24);
if ((j == (m_cap >> 5) - 1) && m_skip) {
int32_t ii;
int32_t count = 4 - (m_cap - m);
__builtin_mma_disassemble_acc((void *)result, &acc7);
SWIZZLE_4x4 for (ii = 0; ii < count; ++ii)
CO[0 * ldc + 28 + ii]
= result_t[0][ii];
if ((n_cap - n) < 3)
for (ii = 0; ii < count; ++ii)
CO[1 * ldc + 28 + ii] = result_t[1][ii];
if ((n_cap - n) < 2)
for (ii = 0; ii < count; ++ii)
CO[2 * ldc + 28 + ii] = result_t[2][ii];
if ((n_cap - n) < 1)
for (ii = 0; ii < count; ++ii)
CO[3 * ldc + 28 + ii] = result_t[3][ii];
} else {
SAVE_ACC_COND_ABSC(&acc7, 28);
}
CO += 32;
} else {
SAVE_ACC_ABSC(&acc0, 0);
SAVE_ACC_ABSC(&acc1, 4);
CO += 8;
SAVE_ACC_ABSC(&acc2, 0);
SAVE_ACC_ABSC(&acc3, 4);
CO += 8;
SAVE_ACC_ABSC(&acc4, 0);
SAVE_ACC_ABSC(&acc5, 4);
CO += 8;
SAVE_ACC_ABSC(&acc6, 0);
SAVE_ACC_ABSC(&acc7, 4);
CO += 8;
}
} else {
if (m_skip || n_skip) {
SAVE_ACC_COND(&acc0, 0);
SAVE_ACC_COND(&acc1, 4);
SAVE_ACC_COND(&acc2, 8);
SAVE_ACC_COND(&acc3, 12);
SAVE_ACC_COND(&acc4, 16);
SAVE_ACC_COND(&acc5, 20);
SAVE_ACC_COND(&acc6, 24);
if ((j == (m_cap >> 5) - 1) && m_skip) {
int32_t ii;
int32_t count = 4 - (m_cap - m);
__builtin_mma_disassemble_acc((void *)result, &acc7);
SWIZZLE_4x4 for (ii = 0; ii < count; ++ii)
CO[0 * ldc + 28 + ii]
= beta * CO[0 * ldc + 28 + ii]
+ alpha * result_t[0][ii];
if ((n_cap - n) < 3)
for (ii = 0; ii < count; ++ii)
CO[1 * ldc + 28 + ii]
= beta * CO[1 * ldc + 28 + ii]
+ alpha * result_t[1][ii];
if ((n_cap - n) < 2)
for (ii = 0; ii < count; ++ii)
CO[2 * ldc + 28 + ii]
= beta * CO[2 * ldc + 28 + ii]
+ alpha * result_t[2][ii];
if ((n_cap - n) < 1)
for (ii = 0; ii < count; ++ii)
CO[3 * ldc + 28 + ii]
= beta * CO[3 * ldc + 28 + ii]
+ alpha * result_t[3][ii];
} else {
SAVE_ACC_COND(&acc7, 28);
}
CO += 32;
} else {
SAVE_ACC(&acc0, 0);
SAVE_ACC(&acc1, 4);
CO += 8;
SAVE_ACC(&acc2, 0);
SAVE_ACC(&acc3, 4);
CO += 8;
SAVE_ACC(&acc4, 0);
SAVE_ACC(&acc5, 4);
CO += 8;
SAVE_ACC(&acc6, 0);
SAVE_ACC(&acc7, 4);
CO += 8;
}
}
AO += k_cap << 5;
BO += k_cap << 2;
}
if (m_skip) goto endloop4;
m_skip = (m & 16) != (m_cap & 16);
if (m_cap & 16) {
uint8_t *BO = B;
v4si_t *rowC;
__vector_quad acc0, acc1, acc2, acc3;
SET_ACC_ZERO4();
vec_t *rowA = (vec_t *)AO;
vec_t *rowB = (vec_t *)BO;
int32_t l;
for (l = 0; l < k_cap / 4; l++) {
MMA(&acc0, rowA[0], rowB[0]);
MMA(&acc1, rowA[1], rowB[0]);
MMA(&acc2, rowA[2], rowB[0]);
MMA(&acc3, rowA[3], rowB[0]);
rowA += 4;
rowB += 1;
}
if (fastpath) {
if (m_skip || n_skip) {
SAVE_ACC_COND_ABSC(&acc0, 0);
SAVE_ACC_COND_ABSC(&acc1, 4);
SAVE_ACC_COND_ABSC(&acc2, 8);
if (m_skip) {
__builtin_mma_disassemble_acc((void *)result, &acc3);
SWIZZLE_4x4 int32_t count = 4 - (m_cap - m);
int32_t ii;
for (ii = 0; ii < count; ++ii)
CO[0 * ldc + 12 + ii] = result_t[0][ii];
if ((n_cap - n) < 3)
for (ii = 0; ii < count; ++ii)
CO[1 * ldc + 12 + ii] = result_t[1][ii];
if ((n_cap - n) < 2)
for (ii = 0; ii < count; ++ii)
CO[2 * ldc + 12 + ii] = result_t[2][ii];
if ((n_cap - n) < 1)
for (ii = 0; ii < count; ++ii)
CO[3 * ldc + 12 + ii] = result_t[3][ii];
} else {
SAVE_ACC_COND_ABSC(&acc3, 12);
}
CO += 16;
} else {
SAVE_ACC_ABSC(&acc0, 0);
SAVE_ACC_ABSC(&acc1, 4);
CO += 8;
SAVE_ACC_ABSC(&acc2, 0);
SAVE_ACC_ABSC(&acc3, 4);
CO += 8;
}
} else {
if (m_skip || n_skip) {
SAVE_ACC_COND(&acc0, 0);
SAVE_ACC_COND(&acc1, 4);
SAVE_ACC_COND(&acc2, 8);
if (m_skip) {
__builtin_mma_disassemble_acc((void *)result, &acc3);
SWIZZLE_4x4 int32_t count = 4 - (m_cap - m);
int32_t ii;
for (ii = 0; ii < count; ++ii)
CO[0 * ldc + 12 + ii] = beta * CO[0 * ldc + 12 + ii]
+ alpha * result_t[0][ii];
if ((n_cap - n) < 3)
for (ii = 0; ii < count; ++ii)
CO[1 * ldc + 12 + ii]
= beta * CO[1 * ldc + 12 + ii]
+ alpha * result_t[1][ii];
if ((n_cap - n) < 2)
for (ii = 0; ii < count; ++ii)
CO[2 * ldc + 12 + ii]
= beta * CO[2 * ldc + 12 + ii]
+ alpha * result_t[2][ii];
if ((n_cap - n) < 1)
for (ii = 0; ii < count; ++ii)
CO[3 * ldc + 12 + ii]
= beta * CO[3 * ldc + 12 + ii]
+ alpha * result_t[3][ii];
} else {
SAVE_ACC_COND(&acc3, 12);
}
CO += 16;
} else {
SAVE_ACC(&acc0, 0);
SAVE_ACC(&acc1, 4);
CO += 8;
SAVE_ACC(&acc2, 0);
SAVE_ACC(&acc3, 4);
CO += 8;
}
}
AO += k_cap << 4;
BO += k_cap << 2;
}
if (m_skip) goto endloop4;
m_skip = (m & 8) != (m_cap & 8);
if (m_cap & 8) {
uint8_t *BO = B;
v4si_t *rowC;
__vector_quad acc0, acc1;
__builtin_mma_xxsetaccz(&acc0);
__builtin_mma_xxsetaccz(&acc1);
vec_t *rowA = (vec_t *)AO;
vec_t *rowB = (vec_t *)BO;
int32_t l;
for (l = 0; l < k_cap / 4; l++) {
MMA(&acc0, rowA[0], rowB[0]);
MMA(&acc1, rowA[1], rowB[0]);
rowA += 2;
rowB += 1;
}
if (fastpath) {
if (m_skip || n_skip) {
SAVE_ACC_COND_ABSC(&acc0, 0);
if (m_skip) {
int32_t ii;
int32_t count = 4 - (m_cap - m);
__builtin_mma_disassemble_acc((void *)result, &acc1);
SWIZZLE_4x4 for (ii = 0; ii < count; ++ii)
CO[0 * ldc + 4 + ii]
= result_t[0][ii];
if ((n_cap - n) < 3)
for (ii = 0; ii < count; ++ii)
CO[1 * ldc + 4 + ii] = result_t[1][ii];
if ((n_cap - n) < 2)
for (ii = 0; ii < count; ++ii)
CO[2 * ldc + 4 + ii] = result_t[2][ii];
if ((n_cap - n) < 1)
for (ii = 0; ii < count; ++ii)
CO[3 * ldc + 4 + ii] = result_t[3][ii];
} else {
SAVE_ACC_COND_ABSC(&acc1, 4);
}
} else {
SAVE_ACC_ABSC(&acc0, 0);
SAVE_ACC_ABSC(&acc1, 4);
}
} else {
if (m_skip || n_skip) {
SAVE_ACC_COND(&acc0, 0);
if (m_skip) {
int32_t ii;
int32_t count = 4 - (m_cap - m);
__builtin_mma_disassemble_acc((void *)result, &acc1);
SWIZZLE_4x4 for (ii = 0; ii < count; ++ii)
CO[0 * ldc + 4 + ii]
= beta * CO[0 * ldc + 4 + ii]
+ alpha * result_t[0][ii];
if ((n_cap - n) < 3)
for (ii = 0; ii < count; ++ii)
CO[1 * ldc + 4 + ii]
= beta * CO[1 * ldc + 4 + ii]
+ alpha * result_t[1][ii];
if ((n_cap - n) < 2)
for (ii = 0; ii < count; ++ii)
CO[2 * ldc + 4 + ii]
= beta * CO[2 * ldc + 4 + ii]
+ alpha * result_t[2][ii];
if ((n_cap - n) < 1)
for (ii = 0; ii < count; ++ii)
CO[3 * ldc + 4 + ii]
= beta * CO[3 * ldc + 4 + ii]
+ alpha * result_t[3][ii];
} else {
SAVE_ACC_COND(&acc1, 4);
}
} else {
SAVE_ACC(&acc0, 0);
SAVE_ACC(&acc1, 4);
}
}
CO += 8;
AO += k_cap << 3;
BO += k_cap << 2;
}
if (m_skip) goto endloop4;
m_skip = (m & 4) != (m_cap & 4);
if (m_cap & 4) {
uint8_t *BO = B;
v4si_t *rowC;
__vector_quad acc0;
__builtin_mma_xxsetaccz(&acc0);
int32_t l;
vec_t *rowA = (vec_t *)AO;
vec_t *rowB = (vec_t *)BO;
for (l = 0; l < k_cap / 4; l++) {
MMA(&acc0, rowA[0], rowB[0]);
rowA += 1;
rowB += 1;
}
if (fastpath) {
if (m_skip || n_skip) {
int32_t count = 4 - (m_cap - m);
int32_t ii;
__builtin_mma_disassemble_acc((void *)result, &acc0);
SWIZZLE_4x4 for (ii = 0; ii < count; ++ii) CO[0 * ldc + ii]
= result_t[0][ii];
if ((n_cap - n) < 3)
for (ii = 0; ii < count; ++ii)
CO[1 * ldc + ii] = result_t[1][ii];
if ((n_cap - n) < 2)
for (ii = 0; ii < count; ++ii)
CO[2 * ldc + ii] = result_t[2][ii];
if ((n_cap - n) < 1)
for (ii = 0; ii < count; ++ii)
CO[3 * ldc + ii] = result_t[3][ii];
} else {
SAVE_ACC_ABSC(&acc0, 0);
}
} else {
if (m_skip || n_skip) {
int32_t count = 4 - (m_cap - m);
int32_t ii;
__builtin_mma_disassemble_acc((void *)result, &acc0);
SWIZZLE_4x4 for (ii = 0; ii < count; ++ii) CO[0 * ldc + ii]
= beta * CO[0 * ldc + ii] + alpha * result_t[0][ii];
if ((n_cap - n) < 3)
for (ii = 0; ii < count; ++ii)
CO[1 * ldc + ii] = beta * CO[1 * ldc + ii]
+ alpha * result_t[1][ii];
if ((n_cap - n) < 2)
for (ii = 0; ii < count; ++ii)
CO[2 * ldc + ii] = beta * CO[2 * ldc + ii]
+ alpha * result_t[2][ii];
if ((n_cap - n) < 1)
for (ii = 0; ii < count; ++ii)
CO[3 * ldc + ii] = beta * CO[3 * ldc + ii]
+ alpha * result_t[3][ii];
} else {
SAVE_ACC(&acc0, 0);
}
}
CO += 4;
AO += k_cap << 2;
BO += k_cap << 2;
}
endloop4:
B += k_cap << 2;
}
return;
}这kernel,写的也太带派了
| 优化技术 | 描述 | 作用 |
|---|---|---|
| 维度填充 | 将矩阵维度 m、n、k 填充到 4 的倍数(m_cap, n_cap, k_cap),使用位运算 (m + 3) & ~3。 |
确保数据对齐,优化矢量化操作,减少边界处理复杂性。 |
| 快速路径优化 | 当 alpha == 1.0 且 beta == 0.0 时,跳过缩放操作,直接存储结果。 |
减少浮点运算,提高性能,适用于常见矩阵乘法场景。 |
| 矢量化与 MMA 指令 | 使用硬件支持的矩阵乘累加(MMA)指令(如 __builtin_mma_xxsetaccz, MMA)并行计算。 |
高效执行 8 位整型矩阵乘累加,最大化硬件并行能力。 |
| 数据重排(Swizzling) | 使用 swizA, swizB, swizC, swizD 等向量重排数据,配合 SWIZZLE_4x4 宏。 |
匹配 MMA 指令的内存布局,提高数据访问效率。 |
| 分块处理 | 将矩阵划分为 16、8、4 行或列的子块,分别处理。 | 适配硬件寄存器和指令限制,提升计算效率。 |
| 边界处理 | 使用 m_skip, n_skip 和条件存储(如 SAVE_ACC_COND)处理非对齐维度。 |
确保非对齐矩阵的正确性,避免覆盖无关数据。 |
| 预取(Prefetching) | 使用 PREFETCH1 宏(如 PREFETCH1(A, 128))提前加载数据到缓存。 |
减少内存访问延迟,提高缓存命中率。 |
在本例中,可以看到oneDNN的不足
- 它的核心在于primitive,即以单个算子为核心的运算。oneDNN没法直接通过一个primitive处理复杂的神经网络(例如MLP中多个matmul和中间的运算)。单个primitive中能处理的算子组合通常是一个复杂操作(例如conv或者matmul),然后在输出接上简单运算(例如relu,bias等等)
- 用户需要手动将计算图划分成不同primitive的组合。例如将
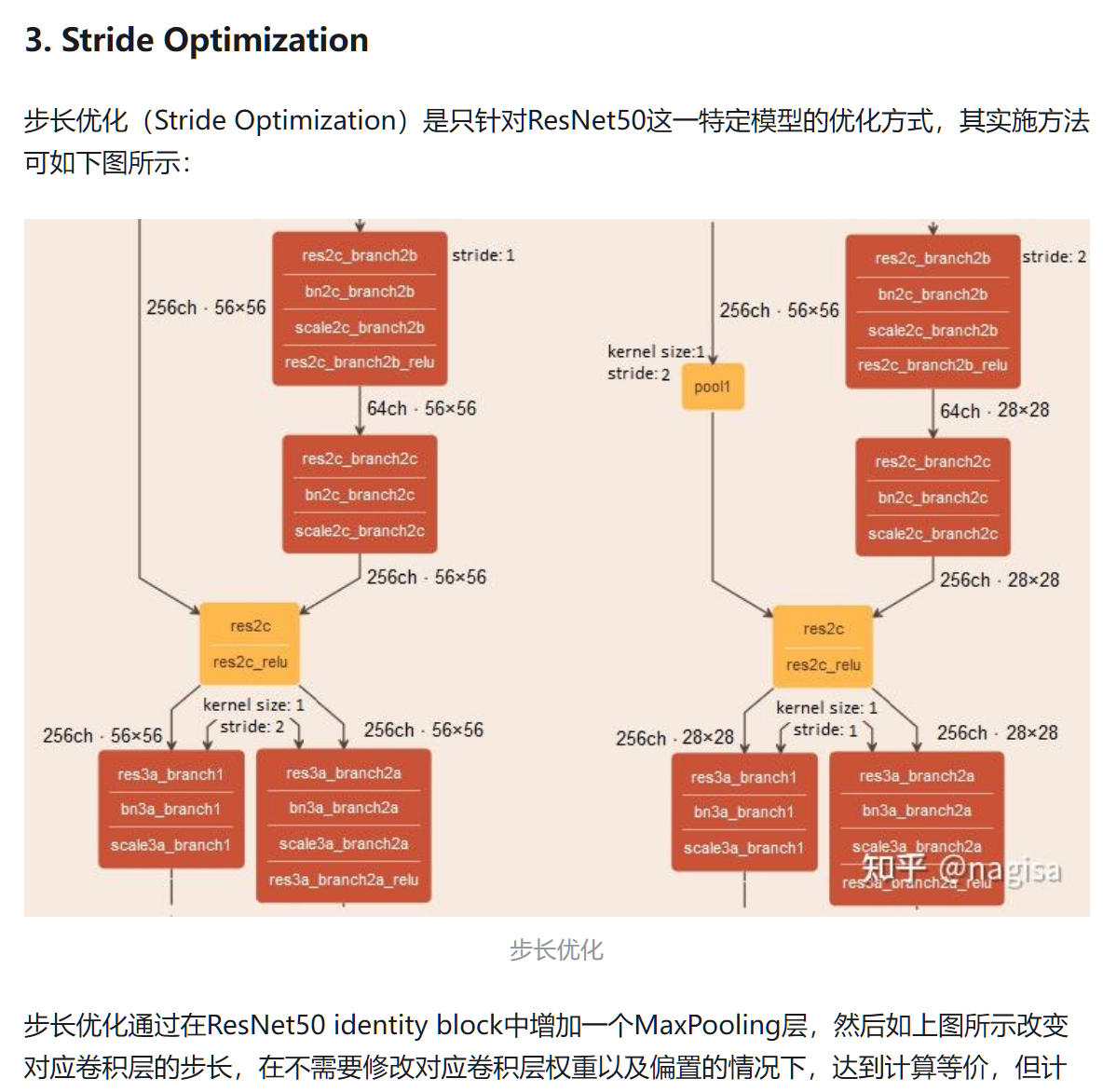
conv, batch norm, relu, conv batch norm, bias划分为conv+batch norm+relu和conv+batch norm+bias。这需要用户非常熟悉oneDNN的API操作,与它的能力限制。 - oneDNN要求复杂算子后连接的简单算子之间的连接关系不能太复杂,简单来说在一个primitive中,基本上只能处理单一线性的图。例如对于以下这个带简单分叉的计算图,oneDNN比较难实现通过单个primitive进行表达
都什么时代了,还在玩传统kernel!
oneDNN Graph Compiler
Microsoft Word - oneDNNGraphCompiler-CGO-Final-For-Publish - V2 - Copy
再见Graph Compiler:AI编译器4年开发经历总结与思考 - 知乎
它结合了传统编译器优化技术和专家调优的微内核(microkernel),用于生成高性能的深度神经网络(DNN)计算图代码
- oneDNN Graph Compiler 设计:
- 混合方法:结合编译器优化(如循环转换、操作融合)和专家调优的微内核(如 gemm_kernel_8bit 这样的矩阵乘法内核),生成高性能代码。
- 两级中间表示(IR):
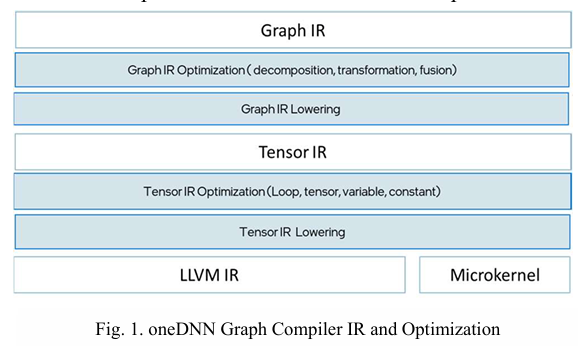
- Graph IR:保留 DNN 操作语义,支持图级优化(如低精度转换、常量权重预处理、操作融合、内存布局传播)。
- Tensor IR:接近 C 语言语义,表示多维数组操作,支持低级代码生成、循环合并和内存缓冲区优化。
- 模板与微内核:
- 使用基于模板的代码生成方法,直接采用专家调优的算法和微内核(如批处理 GEMM 微内核),避免复杂的编译器循环转换。
- 微内核(如 gemm_kernel_8bit)针对硬件寄存器和 L1 缓存优化,处理小块张量计算。
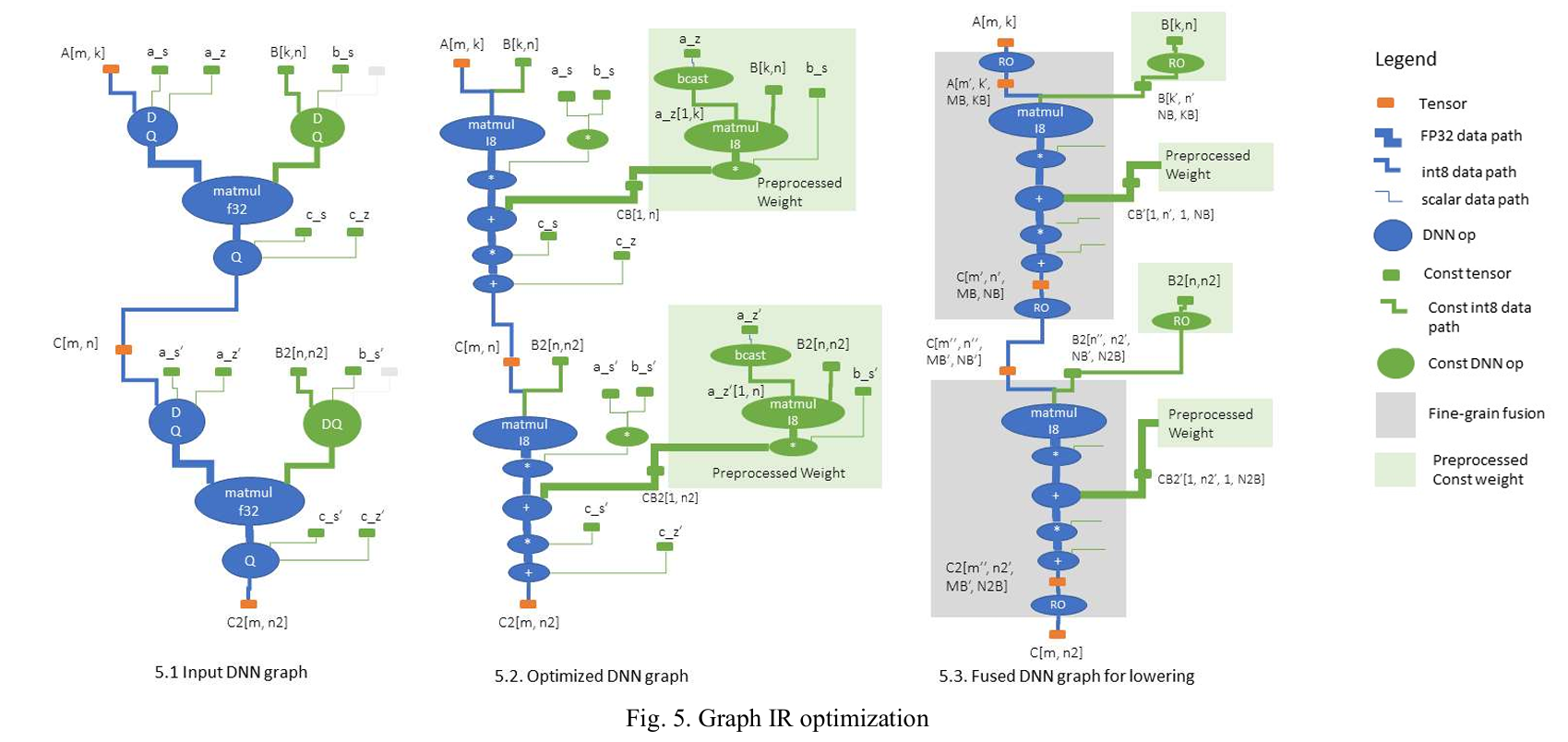
- 操作融合:
- 细粒度融合:将内存密集型操作(如 ReLU、数据重排)融合到计算密集型操作(如矩阵乘法)中,使用模板中的“锚点”(anchor)插入融合操作。
- 粗粒度融合:合并多个操作的并行循环,减少同步开销,提升数据局部性。
- 优化技术(与 gemm_kernel_8bit 相关):
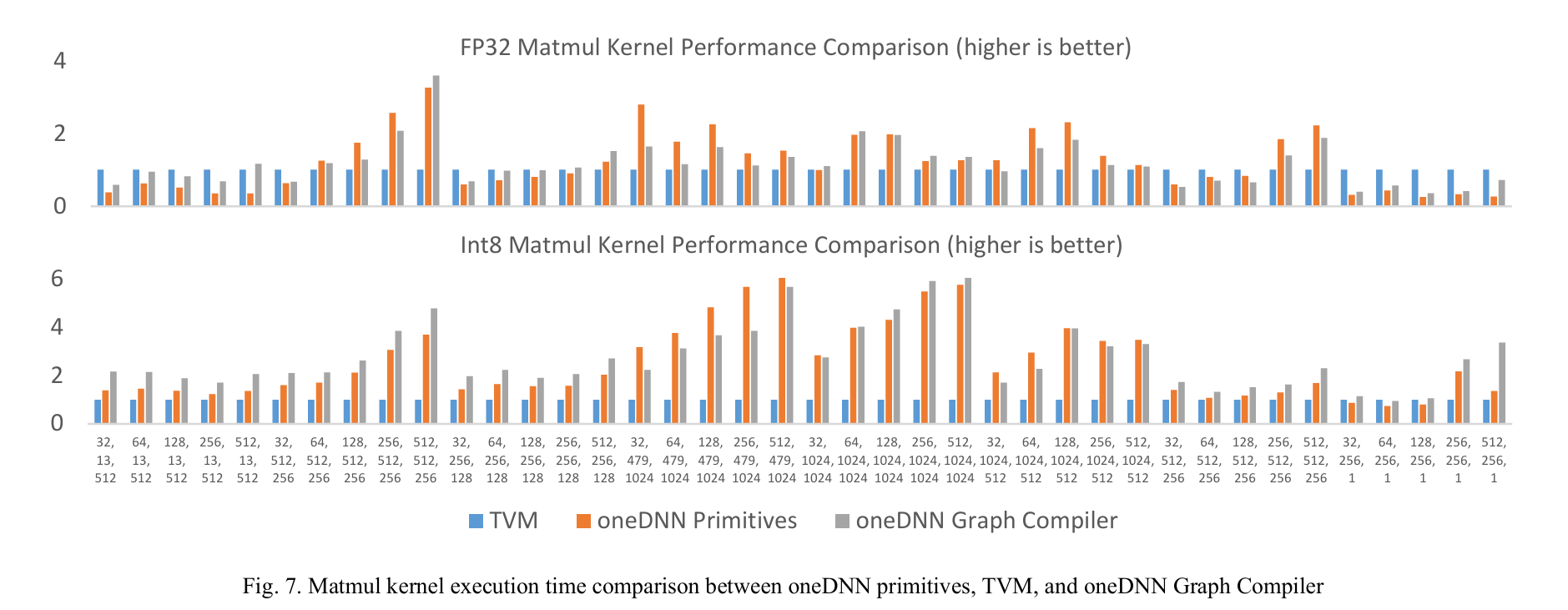
- 低精度计算:支持 Int8 计算(如 gemm_kernel_8bit 中的 8 位整型矩阵乘法),通过分解量化和去量化操作为基本运算(如加法、乘法),减少计算和内存带宽需求。
- 常量权重预处理:识别常量权重(如神经网络权重),在编译时生成预处理函数,运行时重用,减少重复计算。
- 内存布局优化:通过传播优化的块布局(如 gemm_kernel_8bit 中的 swizA 和 swizB 重排),适配硬件指令(如 MMA)的数据需求。
- 内存缓冲区重用:通过生命周期分析重用临时缓冲区,减少内存占用,优化缓存局部性。
- 分块与并行化:将矩阵划分为适配缓存和寄存器的小块(如 gemm_kernel_8bit 中的 MB, NB, KB),并使用多核并行循环。

深入了解 oneDNN 神经网络计算图编译模块 – oneDNN Graph Compiler 第13篇 编译运行Tensor IR - 知乎